机器学习-初级入门（分类算法-决策树）

一、信息增益

1. 熵

   在信息论中，熵（entropy）是随机变量不确定性的度量，也就是熵越大，则随机变量的不确定性越大。设X是一个取有限个值得离散随机变量，其概率分布为：
   
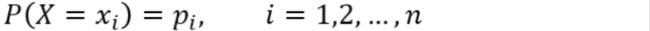
   则随机变量X的熵定义为：
   

2. 条件熵

   设有随机变量（X, Y），其联合概率分布为：
   
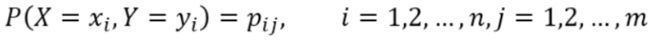
   条件熵H(Y|X)表示在已知随机变量X的条件下，随机变量Y的不确定性。随机变量X给定的条件下随机变量Y的条件熵H(Y|X)，定义为X给定条件下Y的条件概率分布的熵对X的数学期望：
   
   当熵和条件熵中的概率由数据估计得到时（如极大似然估计），所对应的熵与条件熵分别称为经验熵和经验条件熵。

3. 信息增益

   信息增益表示由于得知特征A的信息后儿时的数据集D的分类不确定性减少的程度，定义为：
   
   即集合D的经验熵H(D)与特征A给定条件下D的经验条件熵H(H|A)之差。

   理解：选择划分后信息增益大的作为划分特征，说明使用该特征后划分得到的子集纯度越高，即不确定性越小。因此我们总是选择当前使得信息增益最大的特征来划分数据集。
   缺点：信息增益偏向取值较多的特征（原因：当特征的取值较多时，根据此特征划分更容易得到纯度更高的子集，因此划分后的熵更低，即不确定性更低，因此信息增益更大）
   

二、ID3算法

1. 输入输出

   输入：训练数据集D，特征集A，阈值ε
   输出：决策树T

2. 算法实现步骤

   Step1：若D中所有实例属于同一类$C_k$，则T为单结点树，并将$C_k$类作为该节点的类标记，返回T；

   Step2：若A=Ø，则T为单结点树，并将D中实例数最大的类$C_k$作为该节点的类标记，返回T；

   Step3：否则，计算A中个特征对D的信息增益，选择信息增益最大的特征$A_k$；

   Step4：如果$A_g$的信息增益小于阈值ε，则T为单节点树，并将D中实例数最大的类$C_k$作为该节点的类标记，返回T

   Step5：否则，对$A_g$的每一种可能值$a_i$，依$A_g$=$a_i$将D分割为若干非空子集$D_i$，将$D_i$中实例数最大的类作为标记，构建子结点，由结点及其子树构成树T，返回T；

   Step6：对第i个子节点，以$D_i$为训练集，以A - {$A_g$}为特征集合，递归调用Step1~step5，得到子树$T_i$，返回$T_i$；

三、 C4.5算法

1. 原理
   C4.5算法与ID3算法很相似，C4.5算法是对ID3算法做了改进，在生成决策树过程中采用信息增益比来选择特征。

2. 定义
   我们知道信息增益会偏向取值较多的特征，使用信息增益比可以对这一问题进行校正。

   定义：特征A对训练数据集D的信息增益比GainRatio(D,A)定义为其信息增益Gain(D,A)与训练数据集D的经验熵H(D)之比：
   

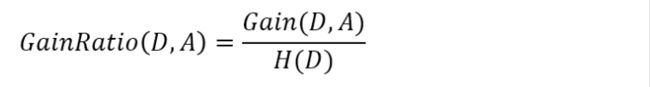
3. 算法实现步骤

   C4.5算法过程跟ID3算法一样，只是选择特征的方法由信息增益改成信息增益比。

四、CART算法

1. Gini指数

   分类问题中，假设有K个类，样本点属于第k类的概率为$P_k$，则概率分布的基尼指数定义为：
   
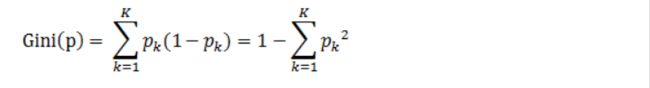
   $P_k$表示选中的样本属于k类别的概率，则这个样本被分错的概率为(1 - $P_k$)对于给定的样本集合D，其基尼指数为：
   
   这里$C_k$是D中属于第k类的样本个数，K是类的个数。
   如果样本集合D根据特征A是否取某一可能值a被分割成D1和D2两部分，即：
   
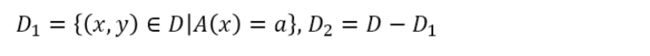
   则在特征A的条件下，集合D的基尼指数定义为：
   
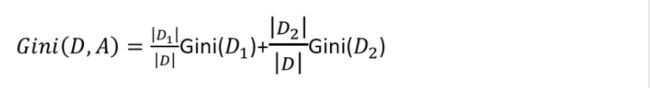
   基尼指数Gini(D)表示集合D的不确定性，基尼指数Gini(D,A)表示经A=a分割后集合D的不确定性。基尼指数值越大，样本集合的不确定性也就越大，这一点跟熵相似。

2. 举例计算Gini系数

   一个包含30个学生的样本，其包含三种特征，分别是：性别（男/女）、班级（IX/X）和高度（5到6ft）。其中30个学生里面有15个学生喜欢在闲暇时间玩板球。那么要如何选择第一个要划分的特征呢，我们通过上面的公式来进行计算。
   
   
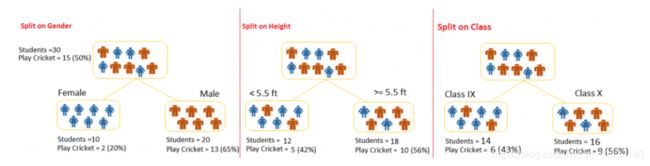
   Gini(D,Gender)最小，所以选择性别作为最优特征。

3. CART算法步骤
   输入输出：

   输入：训练数据集D，停止计算的条件
   输出：CART决策树
   

   实现步骤：

   根据训练数据集，从根结点开始，递归地对每个结点进行以下操作，构建二叉树：

   Step1：设结点的训练数据集为D，计算现有特征对该数据集的基尼指数。此时，对每一个特征A，对其可能取的每个值a，根据样本点A=a的测试为“是”或“否”将D分割为D1和D2两部分，利用上式Gini(D,A)来计算A=a时的基尼指数。

   Step2：在所有可能的特征A以及他们所有可能的切分点a中，选择基尼指数最小的特征及其对应可能的切分点作为最有特征与最优切分点。依最优特征与最有切分点，从现结点生成两个子节点，将训练数据集依特征分配到两个子节点中去。

   Step3：对两个子结点递归地调用Step1、Step2，直至满足条件。

   Step4：生成CART决策树。

   算法停止计算的条件是节点中的样本个数小于预定阈值，或样本集的基尼指数小于预定阈值，或者没有更多特征。

五、实现CART算法代码(别的分割函数可以此为类)

1. 数据

   User ID,Gender,Age,EstimatedSalary,Purchased
   15624510,Male,19,19000,0
   15810944,Male,35,20000,0
   15668575,Female,26,43000,0
   15603246,Female,27,57000,0
   15804002,Male,19,76000,0
   15728773,Male,27,58000,0
   15598044,Female,27,84000,0
   15694829,Female,32,150000,1
   15600575,Male,25,33000,0
   15727311,Female,35,65000,0
   ....
   

2. 代码实现

   import numpy as np
   import pandas as pd
   from collections import Counter
   from sklearn.metrics import confusion_matrix, accuracy_score	
   
   def dataset_format(filename):
       """
       划分训练测试集
       :param filename:文件路径
       :return:
       """
       dataset = pd.read_csv(filename)
       train_data = dataset.sample(frac=0.75, random_state=1, axis=0)
       test_data = dataset[~dataset.index.isin(train_data.index)]
       X_train = train_data.iloc[:, 1:-1].values
       y_train = train_data.iloc[:, -1].values
       X_test = test_data.iloc[:, 1:-1].values
       y_test = test_data.iloc[:, -1].values
       return X_train, y_train, X_test, y_test
   
   
   def one_hot_pre(X, n_c):
       """
   
       :param X: 特征向量
       :param n_c: 第n列要进行one_hot
       :return: 进行one_hot后的数据
       """
       lenth_x, f = X.shape
       catch_encode = dict()  # 记录编码对应类别
       data = X[:, n_c]
       data_set = list(set(data))
       lenth_class = len(data_set)
       if lenth_class == 1:
           X[:, n_c] = 1
           return X
       for index in range(lenth_class):
           catch_encode[index] = data_set[index]
       temp_m = np.zeros((lenth_x, lenth_class))
       for k, v in catch_encode.items():
           index = np.where(X == v)
           temp_m[index[0], k] = 1
       temp_m = temp_m[:, 1:]
       for i in range(lenth_class - 1):
           X = np.insert(X, n_c + i, values=temp_m[:, i], axis=1)
       X = np.delete(X, n_c + lenth_class - 1, axis=1)
       return X
   
   def gini(y):
       """
       :param y:
       :return:
       """
       lenth = y.shape[0]
       counter = Counter(y)  # 计数字典
       res = 0.0
       for num in counter.values():
           p = num / lenth
           res += p ** 2
       return 1 - res
   
   class Tree(object):
       """
       二叉树
       """
       def __init__(
               self,
               value=None,
               true_branch=None,
               false_branch=None,
               results=None,
               col=-1,
               summary=None,
               data=None
       ):
           """
           :param value: 节点划分数据
           :param true_branch: 左分支
           :param false_branch: 右分支
           :param results: 叶子节点的分类结果
           :param col: 对数据某一列特征分割
           :param summary: 简要
           :param data: 叶节点数据
           """
           self.value = value
           self.true_branch = true_branch
           self.false_branch = false_branch
           self.results = results,
           self.col = col
           self.summary = summary
           self.data = data
   
       def __str__(self):
           # print(self.col, self.value)
           # print(self.results)
           # print(self.summary)
           return ""
   
   
   def split_datas(X, y, feature_value, feature_index):
       """
       :param X: 待分割特征
       :param y: 待分割标签
       :param feature_value: 分割值
       :param feature_index: 分割列序号
       :return: 分割成左右分支
       """
       temp = X[:, feature_index]
       if isinstance(feature_value, int) or isinstance(feature_value, float):
           right_list = (X[temp > feature_value], y[temp > feature_value])
           left_list = (X[temp <= feature_value], y[temp <= feature_value])
       else:
           right_list = (X[temp == feature_value], y[temp == feature_value])
           left_list = (X[temp != feature_value], y[temp != feature_value])
       return right_list, left_list
   
   
   def build_decision_tree(X, y, evaluation_function=gini):
       """
       构建二叉树的过程
       :param X: 训练集特征数据
       :param y: 训练集标签
       :param evaluation_function: 选择分割函数
       :return: 训练好的二叉树
       """
       m, n = X.shape
       best_gain = 0.0
       best_val = None
       best_set = None
       current_gain = evaluation_function(y)
       for feature_index in range(n):
           feature_set = set(X[:, feature_index])
           for feature_value in feature_set:
               right_split, left_split = split_datas(X, y, feature_value, feature_index)
               p = right_split[0].shape[0] / m
               gini_d_a = p * evaluation_function(right_split[1]) + (1 - p) * evaluation_function(left_split[1])
               gain = current_gain - gini_d_a
               if gain > best_gain:
                   best_gain = gain
                   best_val = (feature_index, feature_value)
                   best_set = (right_split, left_split)
       dc_y = {
           'impurity': '%.3f' % current_gain,
           'sample': '%d' % m
       }
       if best_gain > 0:
           true_branch = build_decision_tree(best_set[0][0], best_set[0][1], evaluation_function)
           false_branch = build_decision_tree(best_set[1][0], best_set[1][1], evaluation_function)
           return Tree(col=best_val[0], value=best_val[1], true_branch=true_branch, false_branch=false_branch, summary=dc_y)
       else:
           return Tree(results=Counter(y), summary=dc_y, data=(X, y))
   
   
   def classify(data, tree):
       if tree.results[0]:
           return tree.results[0]
       else:
           v = data[tree.col]
           if isinstance(v, int) or isinstance(v, float):
               if v >= tree.value:
                   branch = tree.true_branch
               else:
                   branch = tree.false_branch
           else:
               if v == tree.value:
                   branch = tree.true_branch
               else:
                   branch = tree.false_branch
           return classify(data, branch)
   
   
   def prune(tree, mini_gain, evaluation_function=gini):
       """
       剪支
       :param tree:
       :param mini_gain:
       :param evaluation_function:
       :return:
       """
       if not tree.true_branch.results[0]:
           prune(tree.true_branch, mini_gain, evaluation_function)
       if not tree.false_branch.results[0]:
           prune(tree.false_branch, mini_gain, evaluation_function)
       if tree.true_branch.results[0] and tree.false_branch.results[0]:
           true_branch_lenth = tree.true_branch.data[0].shape[0]
           false_branch_lenth = tree.false_branch.data[0].shape[0]
           p = true_branch_lenth / (true_branch_lenth + false_branch_lenth)
           conn_true_false = np.concatenate((tree.true_branch.data[1], tree.false_branch.data[1]), axis=0)
           true_false_branch_gini = evaluation_function(conn_true_false)
           true_branch_gini = evaluation_function(tree.true_branch.data[1])
           false_branch_gini = evaluation_function(tree.false_branch.data[1])
           gain = true_false_branch_gini - p * true_branch_gini - (1 - p) * false_branch_gini
           if gain < mini_gain:
               # 当节点的gain小于给定的 mini Gain时则合并这两个节点
               tree.data = (
                   np.concatenate((tree.true_branch.data[0], tree.false_branch.data[0]), axis=0),
                   np.concatenate((tree.true_branch.data[1], tree.false_branch.data[1]), axis=0)
               )
               tree.results = Counter(tree.data[1])
               tree.true_branch = None
               tree.false_branch = None
   
   
   def peride(X, model):
       m, n = X.shape
       y_hat = np.zeros((m, 1))
       for i in range(m):
           try:
               y_hat[i] = list(classify(X[i, :], model).keys())
           except Exception:
               pass
       return y_hat
   
   
   decistion_tree = build_decision_tree(X_train, y_train, evaluation_function=gini)
   # prune(decistion_tree, 0.4)
   y_hat = peride(X_test, decistion_tree)
   cm = confusion_matrix(y_test, y_hat)
   accuracy = accuracy_score(y_test, y_hat)
   print("混淆矩阵:\n", cm)
   print("准确度:\n", accuracy)
   

   输出结果：

   混淆矩阵:
    [[56  7]
    [ 6 31]]
   准确度:
    0.87