LeetCode 第 194 场周赛
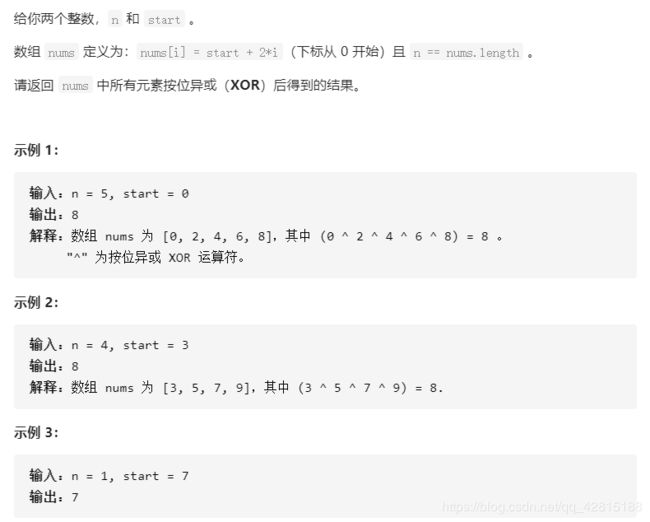
1486.数组异或操作
题目链接:点击这里

class Solution {
public:
int xorOperation(int n, int start) {
int ans = 0;
for(int i = 0; i < n; i++) {
ans ^= start + 2 * i;
}
return ans;
}
};
1487.保证文件名唯一
题目链接:点击这里


最暴力的思路:如果文件名没有出现过,直接使用即可;如果之前出现过,那就添加后缀直到没有出现过为止。
超时代码如下:
class Solution {
public:
vector<string> getFolderNames(vector<string>& names) {
unordered_set<string> hash;
vector<string> ans;
for(auto it : names) {
string s;
int k = 0;
while(hash.count(it + s)) {
k++;
s = "(" + to_string(k) + ")";
}
ans.push_back(it + s);
hash.insert(it + s);
}
return ans;
}
};
优化:我们可以把 “onepiece(1)”, “onepiece(2)”, “onepiece(3)”… 这些文件名出现的次数都加到 “onepiece” 这个文件名上,这样一旦发生冲突,就不用从头开始搜了。
尤其对这样的输入样例 [“onepiece”,“onepiece”,“onepiece”,“onepiece”,“onepiece”] 很有效果。
AC代码如下:
class Solution {
public:
vector<string> getFolderNames(vector<string>& names) {
unordered_map<string, int> p;
vector<string> ans;
for(auto it : names) {
int t = p[it];
if(!t) {
p[it]++;
ans.push_back(it);
}
else {
for(int i = t; ; i++) {
string tmp = it;
tmp += "(" + to_string(i) + ")";
p[it]++;
if(!p[tmp]) {
p[tmp]++;
ans.push_back(tmp);
break;
}
}
}
}
return ans;
}
};
1488.避免洪水泛滥
题目链接:点击这里


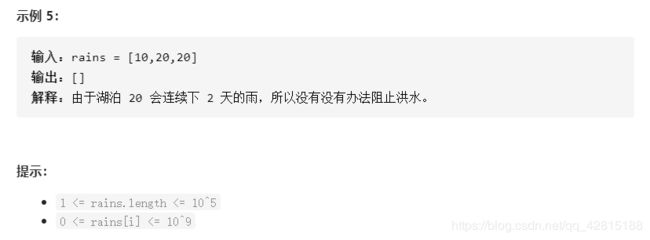
思路:贪心策略,不下雨时,优先抽干最近要下雨的湖泊。
超时代码如下:
class Solution {
public:
vector<int> avoidFlood(vector<int>& rains) {
unordered_map<int,int> p;
vector<int> ans;
for(int i = 0; i < rains.size(); i++) {
if(rains[i] > 0) { // 下雨
if(p[rains[i]] == 0) { // 若湖泊为空,就把它装满
ans.push_back(-1);
p[rains[i]] = 1;
}
else { // 湖泊已满,直接退出
return {};
}
}
else { // 不下雨
int j = i + 1;
while(j < rains.size()) { // 找到其后面最近的要下雨的已满湖泊,把它抽干
if(rains[j] != 0 && p[rains[j]] != 0) {
break;
}
j++;
}
if(j >= rains.size()) ans.push_back(1);
else {
ans.push_back(rains[j]);
p[rains[j]] = 0;
}
}
}
return ans;
}
};
超时代码的瓶颈在于如何快速找到后面最近的要下雨的已满湖泊,本题数据范围为 1 0 5 10^5 105,提示我们时间复杂度为 O ( n log n ) O(n\log n) O(nlogn),因此,借助小根堆可以完美实现该操作。
需要预处理一下,倒着遍历数组,为每一个下雨的湖泊在其后面找到最近的一个下雨天。
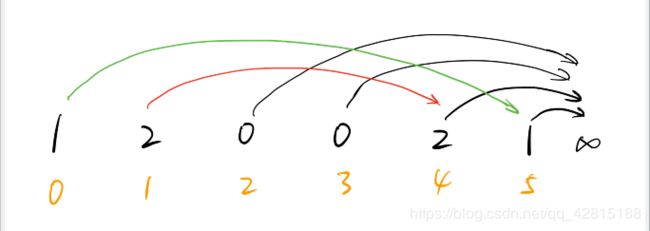
AC代码如下:
class Solution {
public:
vector<int> avoidFlood(vector<int>& rains) {
int n = rains.size();
unordered_map<int,int> day;
vector<int> next(n, 1e9);
for(int i = n - 1; i >= 0; i--) {
int r = rains[i];
if(r) {
if(day.count(r)) next[i] = day[r];
day[r] = i;
}
}
priority_queue<pair<int,int>, vector<pair<int,int>>, greater<pair<int,int>>> heap; // 小根堆
unordered_map<int, bool> st;
vector<int> ans;
for(int i = 0; i < n; i++) {
int r = rains[i];
if(r) {
if(st[r]) return {};
st[r] = true;
heap.push({next[i], r});
ans.push_back(-1);
}
else {
if(heap.empty()) ans.push_back(1);
else {
auto t = heap.top();
heap.pop();
st[t.second] = false;
ans.push_back(t.second);
}
}
}
return ans;
}
};
1489.找到最小生成树里的关键边和伪关键边
题目链接:点击这里
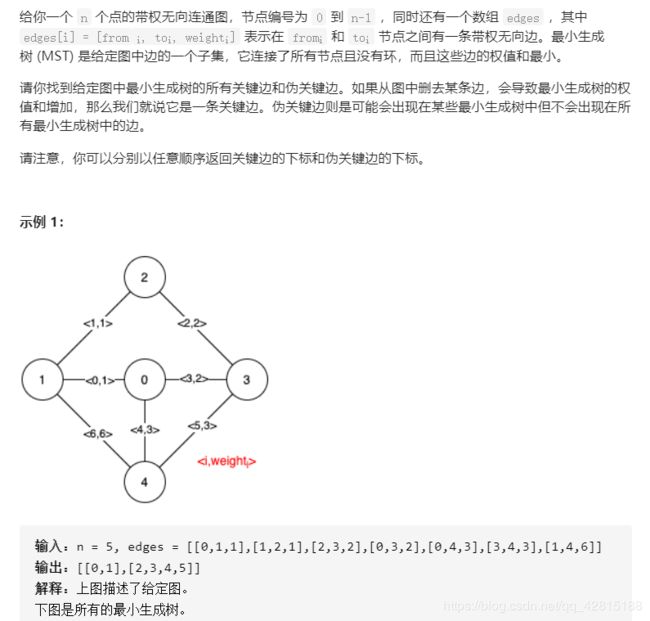
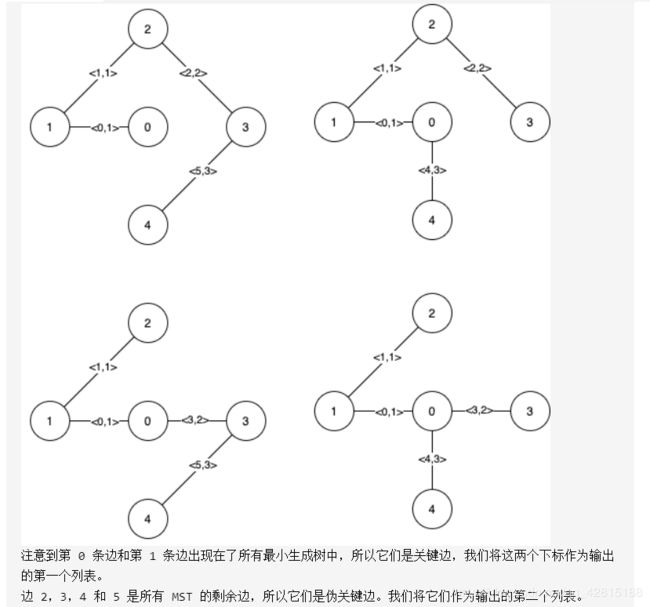
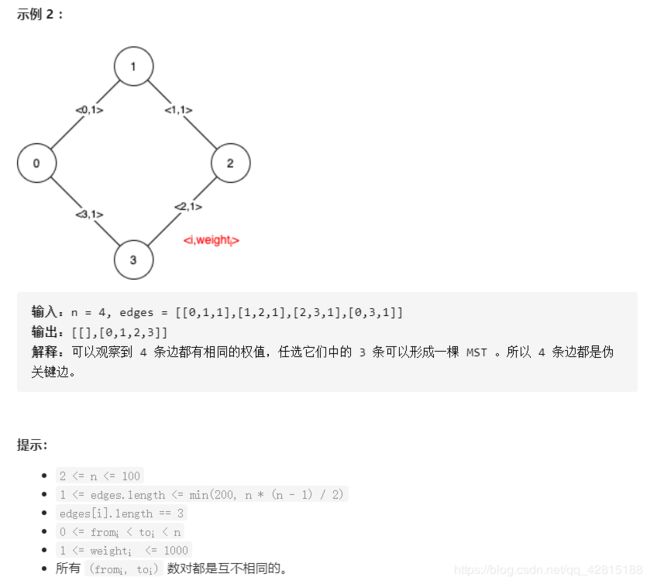
思路:先求出整个图的最小生成树mst,然后根据题目给出的关键边和伪关键边的定义,依次枚举每一条边,看不用该边或必用该边两种情况下的最小生成树是否和mst相等。
class Solution {
public:
int f[110]; // 并查集
int find(int x) {
if(x != f[x]) f[x] = find(f[x]);
return f[x];
}
int work1(int n, vector<vector<int>>& edges, int k) { // 不用第k条边,求最小生成树的值
for(int i = 0; i < n; i++) f[i] = i;
int res = 0, cnt = n;
for(auto e : edges) {
if(e[3] == k) continue; // 遇到第k条边就跳过
int a = e[1], b = e[2], w = e[0];
if(find(a) != find(b)) {
res += w;
cnt--;
f[find(a)] = find(b);
}
}
if(cnt > 1) return INT_MAX;
return res;
}
int work2(int n, vector<vector<int>>& edges, int k) { // 必须用第k条边,求最小生成树的值
for(int i = 0; i < n; i++) f[i] = i;
int res = 0, cnt = n;
for(auto e : edges) {
if(e[3] == k) { // 找到第k条边就一定用
int a = e[1], b = e[2], w = e[0];
if(find(a) != find(b)) {
res += w;
cnt--;
f[find(a)] = find(b);
}
break;
}
}
for(auto e : edges) {
if(e[3] == k) continue;
int a = e[1], b = e[2], w = e[0];
if(find(a) != find(b)) {
res += w;
cnt--;
f[find(a)] = find(b);
}
}
if(cnt > 1) return INT_MAX;
return res;
}
vector<vector<int>> findCriticalAndPseudoCriticalEdges(int n, vector<vector<int>>& edges) {
int m = edges.size();
for(int i = 0; i < m; i++) {
swap(edges[i][0], edges[i][2]); // 默认以第一个元素排序,所以调整一下权值的位置
edges[i].push_back(i); // 添加边的编号
}
sort(edges.begin(), edges.end()); // 按边的权值从小到大排序
int mst = work1(n, edges, -1); // 所有边全用上时,求最小生成树的值
vector<vector<int>> ans(2);
for(int k = 0; k < m; k++) { // 依次枚举每一条边进行判断
if(work1(n, edges, k) != mst) ans[0].push_back(k);
else if(work2(n, edges, k) == mst) ans[1].push_back(k);
}
return ans;
}
};