前几日写了一篇PID算法学习笔记,并幻想了一个场景进行算法仿真。经过不断探索后,博主发现,PID算法的精髓不在算法逻辑,而在于PID三个参数的值。本篇随笔将延续上次的仿真实验进行调试,总结PID调参的规律和方法。
一、调参口诀
先看看百度找到的调参口诀。
参数整定找最佳, 从小到大顺序查。①
先是比例后积分, 最后再把微分加。②
曲线振荡很频繁, 比例度盘要放大。③
曲线漂浮绕大弯, 比例度盘往小扳。④
曲线偏离回复慢, 积分时间往下降。⑤
曲线波动周期长, 积分时间再加长。⑥
曲线振荡频率快, 先把微分降下来。⑦
动差大来波动慢, 微分时间应加长。⑧
理想曲线两个波, 前高后低四比一。⑨
一看二调多分析, 调节质量不会低。⑩
二、调参实战
口诀①,从小到大。根据${PID}$公式可知,积分常数${I}$越大,对输出值影响越小,而比例常数和微分常数越大,对输出值影响越大。
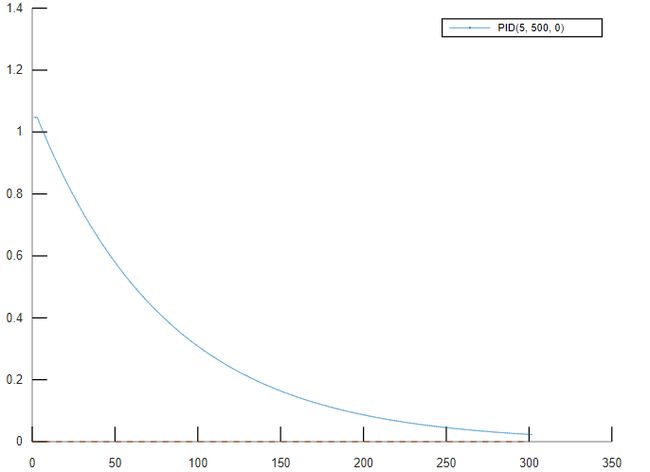
因此,以${(P,I,D)=(5,500,0)}$为初始值,其仿真曲线为
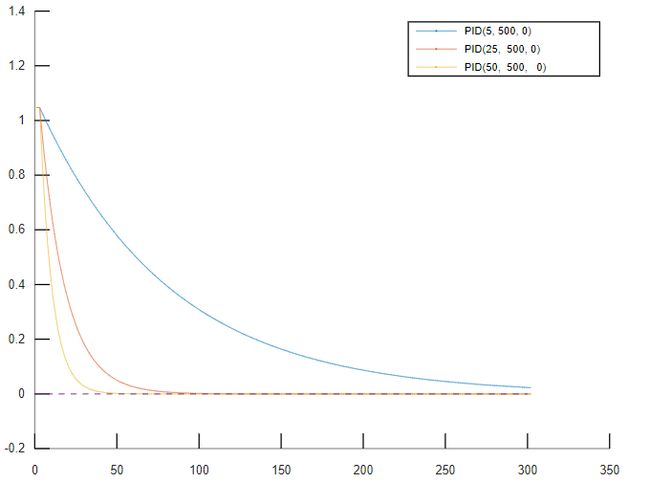
口诀②,先比例。先调节${P}$,分别为5,25,50。
如上图,比例系数越大,曲线越快接近设定值,${P}$为50时,效果最佳。
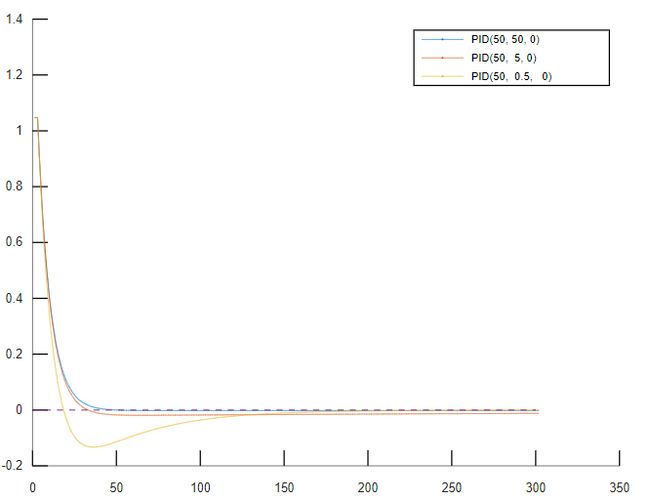
后积分。后调${I}$,分别为50, 5, 0.5
如上图,积分常数P越小,曲线越快达到设定值。当${P}$为0.5时效果最佳
再微分。再调${D}$,分别为0.005, 0.05, 0.5
如上图,${D}$值变大,曲线并没有明显变化。通过上面几次调节,暂时得到一组较优的PID值,为
${PID_{s}=(50,500,0)}$
进一步研究,以该值为基准,改变其中的值。
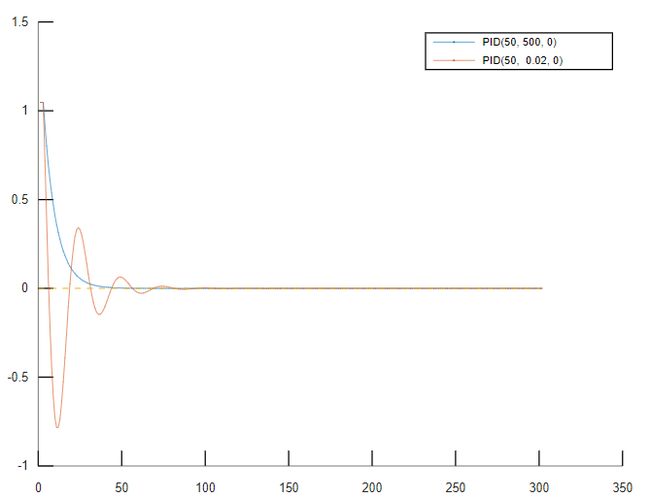
(1)改变P值,改变为500,发现曲线很快超出了设定值,但是如果不考虑稳定性的话,该曲线能更快接近设定值。
(2)改变I值,改变为0.02,发现曲线也会很快超出设定值,后缓慢抖动接近设定值,抖动频率小于曲线(1),根据口诀⑨,这样的曲线可以称作“理想曲线”
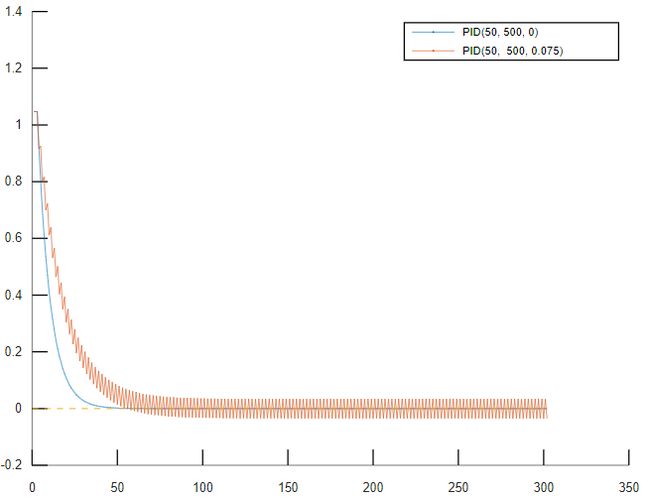
(3)改变${D}$值,改变为0.0.75,曲线剧烈抖动。根据口诀⑦可知,积分系数过大,需要减小。
三、总结
我的数学模型存在很多缺陷,并不能完全模仿真实环境。进行简单的调参后可以发现,P系数调节可能出现“一劳永逸”的情况。而I调节可以减弱P的某些过激行为,比如剧烈抖动变为缓慢震荡,D调节则增强这种行为。本实验中,D系数的作用并不明显,还应在以后的实验中多多观察。
最后,如果调成平均值会发生什么呢?
看,它是不是变得非常强大了……
我,不是说了我不是标题党吗?