perflab实验smooth函数优化

优化1：
一个看到有个函数avg，回想一下书上的例子，减少函数调用算是一个优化，于是就把avg的内容直接写在循环体里面

char smooth_descr[] = "smooth: Current working version";
void smooth(int dim, pixel *src, pixel *dst) 
{
    int i, j;
    for (i = 0; i < dim; i++)
	for (j = 0; j < dim; j++)
	{//不调用avg函数，把avg函数中的内容写在循环体中，把计算结果赋值给dst
	int ii,jj;
	pixel_sum sum;
   	 pixel current_pixel;
  	  initialize_pixel_sum(&sum);
   	 for(ii = max(i-1, 0); ii <= min(i+1, dim-1); ii++) 
	  for(jj = max(j-1, 0); jj <= min(j+1, dim-1); jj++) 
      accumulate_sum(&sum, src[RIDX(ii, jj, dim)]);
  	  assign_sum_to_pixel(¤t_pixel, sum);
  	  dst[RIDX(i,j,dim)] = current_pixel;}
}

我们可以看到avg内部还是有很多函数调用，所以可以预见到这个优化应该是没啥用的:)
看下结果：

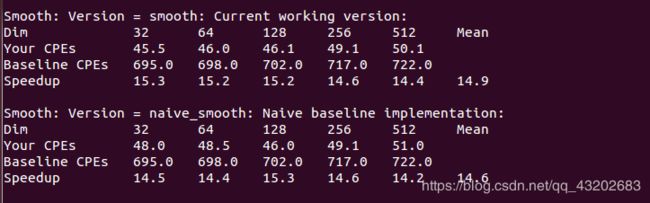
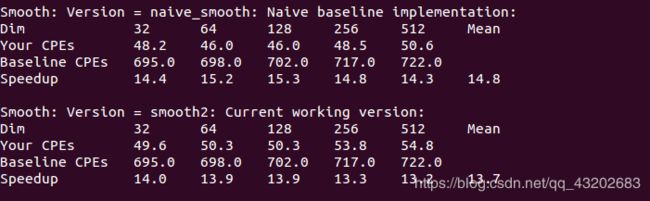
快了0.3，聊胜于无

优化2：
既然avg函数里面还有啰嗦的函数，那我们直接放弃avg函数里面的思想，按照需要实现的功能自己写一下试试。
定义一个函数，功能是求一个矩阵区域分别三种颜色的和，并把得到的和除以指定的num。因为num只有三种可能：四个角落的num是4，第一行，第一列和最后一行，最后一列非角落的格子的num是6，中间部分的num是9，这样就减少了原来对num的存储和运算。

char smooth2_descr[] = "smooth2: Current working version";
pixel cul(int num,int x1,int y1,int x2,int y2,pixel *src,int dim){
	pixel ans;
	int r,b,g;
	r = b = g = 0;
	int ii,jj;
	for(ii = x1;ii <= x2;++ii){
		for(jj = y1;jj <= y2;++jj){
			r += (int)src[RIDX(ii,jj,dim)].red;
			b += (int)src[RIDX(ii,jj,dim)].blue;
			g += (int)src[RIDX(ii,jj,dim)].green;
		}
	}
	r/=num;b/=num;g/=num;
	ans.red=r;ans.blue=b;ans.green=g;
	return ans;
}
void smooth2(int dim, pixel *src, pixel *dst) 
{
    int i, j;
	dst[(RIDX(0,0,dim))] = cul(4,0,0,1,1,src,dim);
	dst[(RIDX(0,dim-1,dim))] = cul(4,0,dim-2,1,dim-1,src,dim);
	dst[(RIDX(dim-1,0,dim))] = cul(4,dim-2,0,dim-1,1,src,dim);
	dst[(RIDX(dim-1,dim-1,dim))] = cul(4,dim-2,dim-2,dim-1,dim-1,src,dim);
	
	for(i = 1;i < dim-1;++i) dst[(RIDX(0,i,dim))] = cul(6,0,i-1,1,i+1,src,dim);
	for(i = 1;i < dim-1;++i) dst[(RIDX(dim-1,i,dim))] = cul(6,dim-2,i-1,dim-1,i+1,src,dim);
	for(i = 1;i < dim-1;++i) dst[(RIDX(i,0,dim))] = cul(6,i-1,0,i+1,1,src,dim);
	for(i = 1;i < dim-1;++i) dst[(RIDX(i,dim-1,dim))] = cul(6,i-1,dim-2,i+1,dim-1,src,dim);
	for (i = 1; i < dim-1; i++)
	for (j = 1; j < dim-1; j++)
	    dst[RIDX(i, j, dim)] = cul(9,i-1,j-1,i+1,j+1,src,dim);
}

来看看结果

哦吼，负优化。

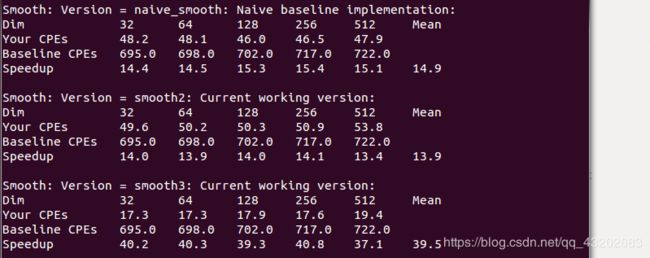
优化3：
优化2用到矩阵求和，我们想要优化矩阵求和的过程，于是就想到了矩阵前缀和，先预处理出矩阵前缀和,f[i][j]表示从(0,0)到(i-1,j-1)这个矩阵全部元素的和，然后任意一个左上方是(x1,y1),右上方是(x2,y2)的矩阵元素和 = f[x2+1][y2+1] - f[x2+1][y1] - f[x1][y2+1] + f[x1][x2]
用这个公式求和来代替优化2中的循环求和函数

int qr[530][530],qb[530][530],qg[530][530];

char smooth3_descr[] = "smooth3: Current working version";

void smooth3(int dim, pixel *src, pixel *dst) 

{



    int i, j;

	for(i = 1;i <= dim;++ i){

		for(j = 1;j <= dim;++j){

			qr[i][j] = qr[i-1][j] + qr[i][j-1] - qr[i-1][j-1] + src[RIDX(i-1,j-1,dim)].red;

			qb[i][j] = qb[i-1][j] + qb[i][j-1] - qb[i-1][j-1] + src[RIDX(i-1,j-1,dim)].blue;

			qg[i][j] = qg[i-1][j] + qg[i][j-1] - qg[i-1][j-1] + src[RIDX(i-1,j-1,dim)].green;

		}
		
	}//求三种颜色的矩阵前缀和

	dst[(RIDX(0,0,dim))].red = qr[2][2]>>2;

	dst[(RIDX(0,0,dim))].blue = qb[2][2]>>2;

	dst[(RIDX(0,0,dim))].green = qg[2][2]>>2;//左上角

	

	dst[(RIDX(0,dim-1,dim))].red = (qr[2][dim] - qr[2][dim-2])>>2;

	dst[(RIDX(0,dim-1,dim))].blue = (qb[2][dim] - qb[2][dim-2])>>2;

	dst[(RIDX(0,dim-1,dim))].green = (qg[2][dim] - qg[2][dim-2])>>2;//右上角

	

	dst[(RIDX(dim-1,0,dim))].red = (qr[dim][2] - qr[dim-2][2])>>2;

	dst[(RIDX(dim-1,0,dim))].blue = (qb[dim][2] - qb[dim-2][2])>>2;

	dst[(RIDX(dim-1,0,dim))].green = (qg[dim][2] - qg[dim-2][2])>>2;//左下角

	

	dst[RIDX(dim-1,dim-1,dim)].red = (qr[dim][dim] - qr[dim-2][dim] - qr[dim][dim-2] + qr[dim-2][dim-2])>>2;

	dst[RIDX(dim-1,dim-1,dim)].blue = (qb[dim][dim] - qb[dim-2][dim] - qb[dim][dim-2] + qb[dim-2][dim-2])>>2;

	dst[RIDX(dim-1,dim-1,dim)].green = (qg[dim][dim] - qg[dim-2][dim] - qg[dim][dim-2] + qg[dim-2][dim-2])>>2;
//右下角
	

	for(i = 1;i < dim-1;++i){//第一行 

		dst[RIDX(0,i,dim)].red = (qr[2][i+2] - qr[2][i-1])/6;

		dst[RIDX(0,i,dim)].blue = (qb[2][i+2] - qb[2][i-1])/6;

		dst[RIDX(0,i,dim)].green = (qg[2][i+2] - qg[2][i-1])/6;

	}

	for(i = 1;i < dim-1;++i){//第一列 

		dst[RIDX(i,0,dim)].red = (qr[i+2][2] - qr[i-1][2])/6;

		dst[RIDX(i,0,dim)].blue = (qb[i+2][2] - qb[i-1][2])/6;

		dst[RIDX(i,0,dim)].green = (qg[i+2][2] - qg[i-1][2])/6;	

	}

	for(i = 1;i < dim-1;++i){//最后一行 

		dst[RIDX(dim-1,i,dim)].red = (qr[dim][i+2] - qr[dim][i-1] - qr[dim-2][i+2] + qr[dim-2][i-1])/6;

		dst[RIDX(dim-1,i,dim)].blue = (qb[dim][i+2] - qb[dim][i-1] - qb[dim-2][i+2] + qb[dim-2][i-1])/6;

		dst[RIDX(dim-1,i,dim)].green = (qg[dim][i+2] - qg[dim][i-1] - qg[dim-2][i+2] + qg[dim-2][i-1])/6;

	}

	for(i = 1;i < dim-1;++i){//最后一列 

		dst[RIDX(i,dim-1,dim)].red = (qr[i+2][dim] - qr[i-1][dim] - qr[i+2][dim-2] + qr[i-1][dim-2])/6;

		dst[RIDX(i,dim-1,dim)].blue = (qb[i+2][dim] - qb[i-1][dim] - qb[i+2][dim-2] + qb[i-1][dim-2])/6;

		dst[RIDX(i,dim-1,dim)].green = (qg[i+2][dim] - qg[i-1][dim] - qg[i+2][dim-2] + qg[i-1][dim-2])/6;

	}

	for(i = 1;i < dim-1;++i){//中间部分

		for(j = 1;j < dim-1;++j){

			dst[RIDX(i,j,dim)].red = (qr[i+2][j+2] - qr[i+2][j-1] - qr[i-1][j+2] + qr[i-1][j-1])/9;

			dst[RIDX(i,j,dim)].blue = (qb[i+2][j+2] - qb[i+2][j-1] - qb[i-1][j+2] + qb[i-1][j-1])/9;

			dst[RIDX(i,j,dim)].green = (qg[i+2][j+2] - qg[i+2][j-1] - qg[i-1][j+2] + qg[i-1][j-1])/9;

		}

	}

}

忐忑的心情按下./driver

从14.9优化到了39.5，效果拔群，开心