优先级队列(堆)
文章目录
- 1.队列的几种类型
- 2.二叉树的顺序存储
- 2.1存储方式
- 2.2下标关系:
- 3.堆
- 3.1概念
- 3.2向下调整
- 3.3建堆
- 3.堆的应用-优先级队列
- 3.1模拟实现优先级队列
- 3.2java 中的优先级队列
- 4.堆的其他应用-TopK 问题
- 5.OJ题-查找和最小的K对数字
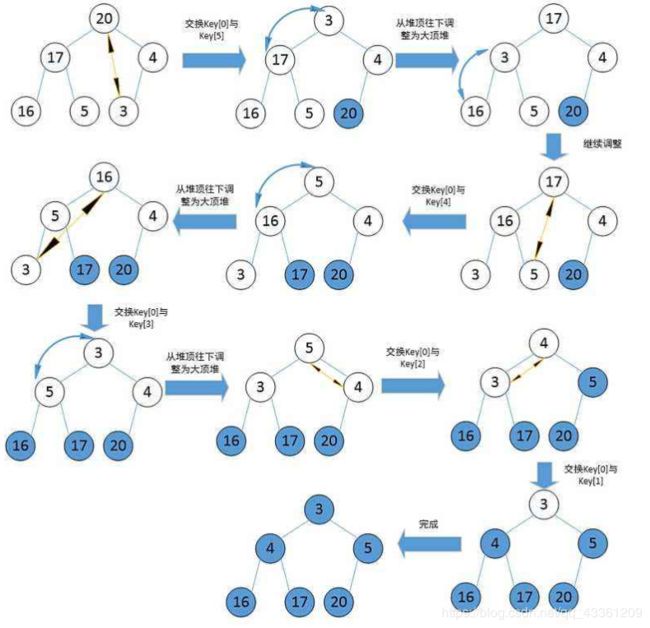
- 6.堆的其他应用-堆排序
1.队列的几种类型
1,普通队列:先进先出。
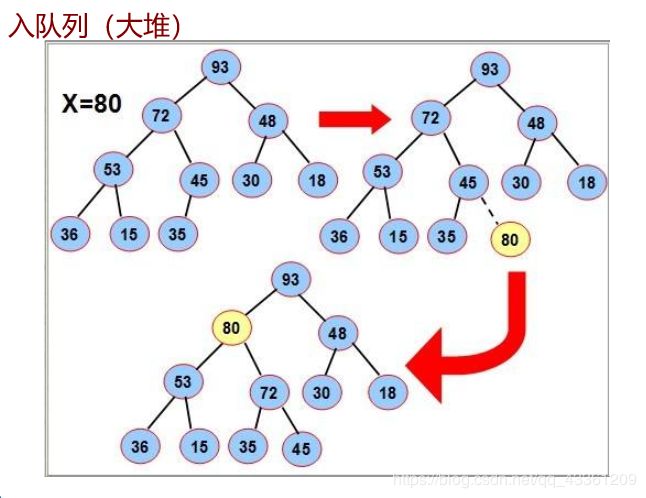
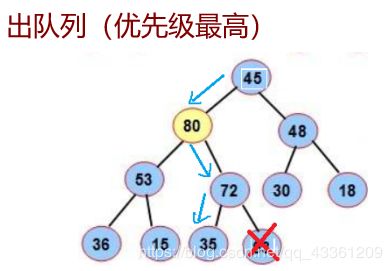
2,带优先级的队列:优先级高的先出队列,优先级一样时按照先进先出的规则。
3,带类型的队列
4,阻塞队列:线程安全版本的队列,具有一定的特性(队列为空,取元素发生阻塞;队列满,插入元素)。
5,无锁队列:线程安全版本的队列,不用加锁就可以保证线程安全。
2.二叉树的顺序存储
2.1存储方式
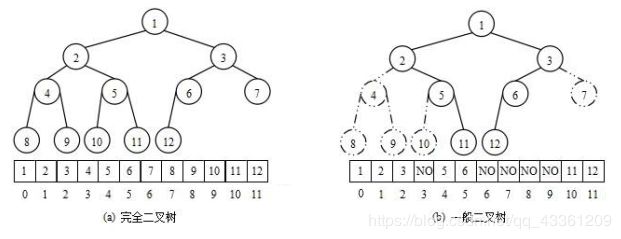
使用数组保存二叉树结构,方式即将二叉树用层序遍历方式放入数组中。
一般只适合表示完全二叉树,因为非完全二叉树会有空间的浪费。
2.2下标关系:
左子树下标 = 根节点下标 * 2 + 1
右子树下标 = 根节点下标 * 2 + 2
根节点下标 = (孩子节点下标 - 1) / 2
3.堆
3.1概念
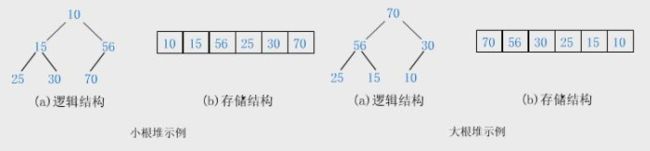
1,堆逻辑上是一棵完全二叉树
2,堆物理上是保存在数组中
3,满足任意结点的值都大于其子树中结点的值,叫做大堆,或者大根堆,或者最大堆
4,反之,则是小堆,或者小根堆,或者最小堆
5,堆的基本作用是,快速找集合中的最值(TOP K问题)
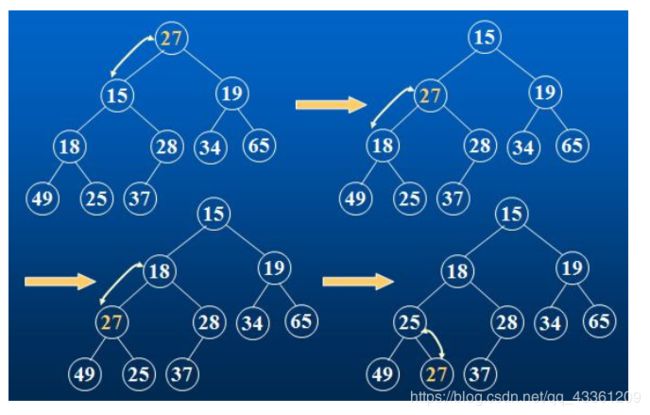
3.2向下调整
前提:左右子树必须已经是一个堆(完全二叉树),才能调整。
说明:
- array 代表存储堆的数组
- size 代表数组中被视为堆数据的个数
- index 代表要调整位置的下标
// 小堆 向下调整
// 通过 size 指定 array 中哪些元素是有效的堆元素
// index 表示从哪个位置的下标开始调整
// 左右子树都是堆, 才能进行这样的调整.
public static void shiftDown(int[] array, int size, int index) {
int parent = index;
int child = 2 * parent + 1; // 根据 parent 下标找到左子树的下标
while (child < size) {
// 比较左右子树, 找到较小值
if (child + 1 < size && array[child + 1] < array[child]) {
child = child + 1;
}
// 经过上面的比较, 已经不知道 child 是左子树还是右子树了.
// 知道的是 child 下标一定对应左右子树最小值的下标.
// 拿 child 位置的元素和 parent 位置的元素进行比较
if (array[child] < array[parent]) {
// 不符合小堆的规则, 就交换父子节点
int tmp = array[child];
array[child] = array[parent];
array[parent] = tmp;
} else {
// 调整完毕, 不需要继续了
break;
}
// 更新 parent 和 child, 处理下一层的数据(child位置可能破坏堆性质).
parent = child;
child = parent * 2 + 1;
}
}
// 大堆 向下调整
public static void shiftDown1(int[] array, int size, int index){
int parent = index;
int child = 2*parent +1 ; //左子树
while(child < size){ // 孩子节点存在
if(child + 1 < size && array[child +1] > array[child]){
child = child+1; //右子树存在且右子树大
}
if (array[child] < array[parent]) {
// 不符合大堆的规则, 就交换父子节点
int tmp = array[child];
array[child] = array[parent];
array[parent] = tmp;
} else {
// 父节点大不需要调整, 不需要继续了
break;
}
// 更新 parent 和 child, 处理下一层的数据.
parent = child;
child = parent * 2 + 1;
}
}
3.3建堆
注意:
从前向后遍历,向上调整
从后向前遍历,向下调整
public static void createHeap(int[] array, int size) {
//向下调整 需要从后向前遍历
for (int i = (size - 1 - 1) / 2; i >= 0; i--) {
shiftDown(array, size, i);
}
}
3.堆的应用-优先级队列
3.1模拟实现优先级队列
3.2java 中的优先级队列
PriorityQueue implements Queue
4.堆的其他应用-TopK 问题
拜托,面试别再问我TopK了!!!
给定 100 亿数字,求前 1000 大的元素?( 400亿字节 ≈ 40G空间)
答:使用方案二。
方案一:用一个数组保存刚才这些数字,直接在这个数组上建大堆。循环 1000 次进行取堆顶元素+向下调整,就可以得到前 1000 大的元素。
耗空间:空间不一定充足,内存可能发不下
耗时间:100 亿数字建堆肯定比 1000 个数字建堆慢
方案二:先取集合中前 1000 个元素放到一个数组中,建立一个小堆。再一个个遍历集合中的数字,依次和堆顶元素比较,只要比堆顶元素大,就删除堆顶元素(调整堆),再把当前元素入堆(调整堆)。当所有元素遍历结束时,堆中的元素就是前 1000 大的元素。
时间复杂度分析(N >> M)
方案一:O(N) + O(M * log(N)) //建堆 + 遍历*堆调整
方案二:O(M) + O(N * log(M)) // 建堆 + 遍历*堆调整
5.OJ题-查找和最小的K对数字
题目链接:查找和最小的K对数字
需要把数对放到一个类中,优先队列用来保存类的对象即可。
import java.util.ArrayList;
import java.util.List;
import java.util.PriorityQueue;
class Pair implements Comparable<Pair>{
public int n1;
public int n2;
public int sum;
public Pair(int n1, int n2){
this.n1 = n1;
this.n2 = n2;
this.sum = n1+n2;
}
@Override
public int compareTo(Pair o) {
return this.sum-o.sum;
}
}
public class Solution {
public List<List<Integer>> kSmallestPairs(int[] nums1, int[] nums2, int k) {
List<List<Integer>> result = new ArrayList<>();
if(nums1.length == 0 || nums2.length ==0 || k<=0){
return result;
}
// 前 k 小元素,建立小堆
PriorityQueue<Pair> queue = new PriorityQueue<>(); // 默认小堆
// 采取方式1
for(int i = 0; i < nums1.length; i++){
for(int j = 0; j < nums2.length; j++){
queue.offer(new Pair(nums1[i],nums2[j]));
}
}
// 一定要队列不为空才可以取 k有可能大于数对数
for(int i = 0; i < k && !queue.isEmpty(); i++){
Pair cur = queue.poll();
List<Integer> l = new ArrayList<>();
l.add(cur.n1);
l.add(cur.n2);
result.add(l);
}
return result;
}
}