100行代码实现MerkleTree！

Merkle树作为区块链中重要的数据结构，有着很广泛的应用。

基本就是每个叶节点作为数据存储点，对它进行哈希之后，得到最初的叶子节点，再两两相加哈希，一直类推，到只剩一个节点，即根节点即可。

说到哈希啊，就不得不提到祖师爷Leslie Lamport：

就当你发现Hash、LaTex，拜占庭将军问题、Paxos都是一个人搞出来的之后，那种五体投地的感觉....orz

Leslie Lamport在1973年第一个提出hash签名方案，hash有多伟大就不用说了吧。

Merkle树其实最早不是应用在区块链中的，Ralph Merkle：

他最先提出Merkle树应用在数字签名中：Merkle提出一种方法可以保持签名N条不同的消息的能力，而公钥成本没有爆炸性增长。Merkle的方法大概类似这种： 

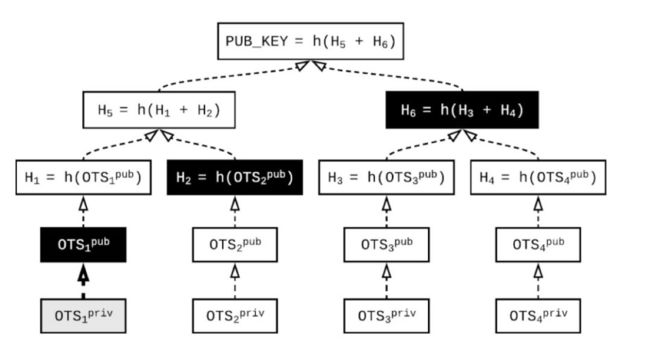
Merkle树在这里有一个粗略的描述：它们提供了一种方法，用这种方法可以收集很多不同的值，这样这些值可以由单个“根”散列表示。给出这个散列值，就很容易生成一个元素在hash树中的简单的证明，这个证明的大小是树中叶节点的个数。比如说上图，我要验证OTS1是否正确，我只需要验证图中黑色的H2和H6即可，根据H2和H6我们就能哈希出树根，对比区块中的树根是否一致即可。

那么如何应用在区块链中呢？

我们知道啊，区块链中的数据和交易量都是非常大的，一般情况下，一个区块中包含几百上千笔交易是很常见的。由于区块链的去中心化特性，网络中的每个节点必须是独立，自给自足的，也就是每个节点必须存储一个区块链的完整副本。那么随着越来越多的交易，以及越来越多的挖矿，数据存储成为了一笔巨大的开销。

如何缩小这笔开销呢？

区块链中每个区块都会有一个 Merkle 树，它从叶节点开始，一个叶节点就是一个交易哈希。叶节点的数量必须是双数，但是并非每个块都包含了双数的交易。如果一个块里面的交易数为单数，那么就将最后一个叶节点（也就是Merkle树的最后一个交易，不是区块的最后一笔交易）复制一份凑成双数。

从下往上，两两成对，连接两个节点哈希，将组合哈希作为新的哈希。新的哈希就成为新的树节点。重复该过程，直到仅有一个节点，也就是树根。根哈希然后就会当做是整个块交易的唯一标示，将它保存到区块头，然后用于工作量证明。

也就是说，我们不必存储所有的交易信息在区块中，只需存储Merkle树根就行了，大大减小了存储量。

 

像上图这样，就不用把所有交易存储下来啦~

那么，如何用代码优雅的实现它呢？

Merkle树有一个特点，初始化时它的叶节点个数必须是双数，如果不是双数，那么复制最后一个叶节点凑成双。

---

Duang~代码来了

老规矩，先引入包：

package main

import (
  "crypto/sha256"
  "fmt"
  "strconv"
)

定义Merkle树和树节点数据结构：

type MerkleTreeNode struct {
  Data  []byte
  Hash  []byte
  Left  *MerkleTreeNode
  Right *MerkleTreeNode
}

type MerkleTree struct {
  Root *MerkleTreeNode
}

实现一个队列，简单的Push和Pop，方便建树，因为建树肯定是每次两两合并，新生成的节点放后面，类似于哈夫曼树建树过程：

type Queue struct {
  List []MerkleTreeNode
}

func NewQueue() *Queue {
  list := make([]MerkleTreeNode, 0)
  return &Queue{list}
}

func (q *Queue) Push(node *MerkleTreeNode) {
  q.List = append(q.List, *node)
}

func (q *Queue) Pop() *MerkleTreeNode {
  if q.Len() == 0 {
    panic("Empty!")
  }
  node := q.List[0]
  q.List = q.List[1:]
  return &node
}

func (q *Queue) Len() int {
  return len(q.List)
}

生成Merkle树节点部分，注意啊，因为Merkle树是一种完全二叉树，所以它的节点只有两种情况：两个孩子的非叶节点和无孩子的叶节点：

func NewMerkleTreeNode(left, right *MerkleTreeNode, data []byte) *MerkleTreeNode {
  var node MerkleTreeNode

  if left == nil && right == nil {
    hash := sha256.Sum256(data)
    node.Hash = hash[:]
  } else {
    childHash := append(left.Hash, right.Hash...)
    hash := sha256.Sum256(childHash)
    node.Hash = hash[:]
  }

  node.Left = left
  node.Right = right
  node.Data = data
  return &node
}

建树函数，使用一个队列来进行建树：

func NewMerkleTree(data [][]byte) *MerkleTree {
  var root MerkleTree
  nodes := NewQueue()
  if len(data)%2 != 0 {
    data = append(data, data[len(data)-1])
  }

  for _, i := range data {
    nodes.Push(NewMerkleTreeNode(nil, nil, i))
  }

  for nodes.Len() > 1 {
    left := nodes.Pop()
    right := nodes.Pop()
    node := NewMerkleTreeNode(left, right, nil)
    nodes.Push(node)
  }
  root.Root = nodes.Pop()
  return &root
}

先序遍历看看咱们建立的树是否成功：

func PreOrderVisit(root *MerkleTreeNode) {
  if root != nil {
    fmt.Print(root.Data)
    PreOrderVisit(root.Left)
    PreOrderVisit(root.Right)
  }
}

写个main函数看看结果呗，建立一个存储6个数据的Merkle树：

func main() {
  data := make([][]byte, 6)
  for i := 0; i < 6; i++ {
    data[i] = []byte(strconv.Itoa(i))
  }
  root := NewMerkleTree(data)
  PreOrderVisit(root.Root)
}

打印看看：

对应的树就是这样子：

好啦，简单的Merkle树就实现了，对于它的插入删除，那就是优化和工程问题了，二叉平衡树啊红黑树啊伸展树啊都可以的，主要是reigns还不能手撸一个红黑树，此事以后再议~

好啦，今天就到这了。

如果对区块链感兴趣，可以关注下面这个公众号哦，推送的全是区块链干货~