贝叶斯滤波算法
bayes filter是一种观测数据和控制数据中计算置信度的通用算法
1.Derivation of Bayes filter
先做一些符号说明
- z = observation
- u = action
- x = state
- P(z|x) P ( z | x ) 观测模型(在状态x下观察到z的概率)
- P(x|u,x′) P ( x | u , x ′ ) 运动转移概率(在x’状态下,执行了动作u之后,状态改变为x的概率)
关于公式数学推导有任何地方不懂可以点击这里,这里直接给出结论
这里的 η η 是根据recusive bayes我自己推导的。
分为两部分
- Prediction step
- correction step
2. Algorithm

我不是很理解为什么这里\eta是这样操作的,与我上面的推导不一样,很奇怪,我不是很理解,这里说\eta是一个归一化的参数,保证所有概率和为1
3. 形象化例子
3.1 机器人小萝卜
这一部分有一些细节我感觉是原文有问题,但是也可能是我理解错了,所以如果下面有一些不懂的地方,希望大家去看原文,也恳请给我留言,一起交流
有这么一个机器人小萝卜,可以沿着一维的路径运动,墙和这个一维路径是平行的,而且墙上开了几个门。
小萝卜装备了
- 检测门的传感器(sensor)
- 并且知道门在墙的那些位置
- 但是在开始前并没有先验置信度。
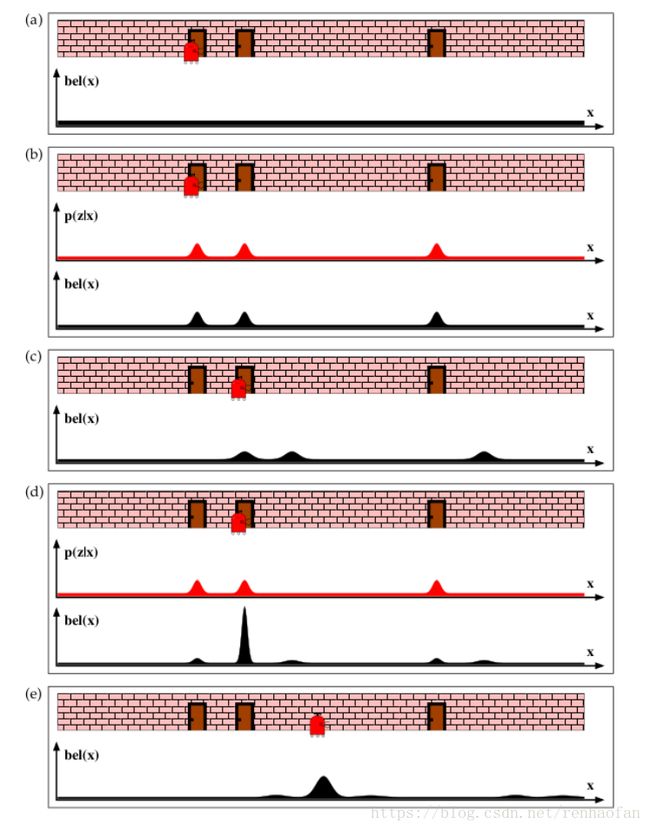
如下图a
那小萝卜怎么确定自己的位置呢?
一, 小萝卜可以使用sensor检测自己是不是在门前面,由于sensor噪声和环境噪声的原因,会有以下几种种情况:
为了看着舒服,先声明一下符号
truth 表示小萝卜在门前
report 表示传感器的检测结果
id: in font of door
nd: not in font of door
(1). Truth–id, Report–id
小萝卜有很大程度确定自己在门前,所以门对应位置的置信度会变得很高,如下图b:
(2).Truth–nd, Report–nd;
原文有四种情况,鉴于其他两种我不会特别理解,这里只提一下其他两种情况真实世界出现的可能性不大,但能部分解释为什么有一些不在门前的位置,概率不为0,我自己理解就是噪声问题,但原文在这两种情况的论述我觉得是有一些我不太能理解的。
二, 小萝卜运动的时候会降低自己对于自己位置确定程度,因为小萝卜要走5米,但实际可能走了4.95米。换句话说小萝卜不可能直接绝对的知道自己到底移动了多少。所以置信度就会出现紊乱。如下图c
三, 小萝卜在第二个门前面测量。根据第一中也就是图a的先验概率,我们和这次的观测值z结合在一起我们更新我们额达置信度,所以在第二个们的x出现了置信度的一个峰值。如图d
四, 小萝卜再次运动,置信度再次出现紊乱
参考:
- SLAM笔记三——贝叶斯滤波器
- udacity
- pdf摘要
- pdf摘要2
- 细说贝叶斯滤波
- 无人驾驶高精度定位技术-递归贝叶斯滤波