深度学习笔记（三）用Torch实现多层感知器

代码地址： https://github.com/vic-w/torch-practice/tree/master/multilayer-perceptron

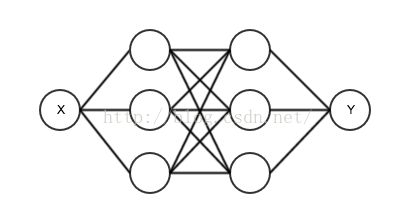
上一次我们使用了输出节点和输入节点直接相连的网络。网络里只有两个可变参数。这种网络只能表示一条直线，不能适应复杂的曲线。我们将把它改造为一个多层网络。一个输入节点，然后是两个隐藏层，每个隐藏层有3个节点，每个隐藏节点后面都跟一个非线性的Sigmoid函数。如图所示，这次我们使用的网络是有2个隐藏层，每层有3个节点的多层神经网络。

那么这样的结构用代码如何表示呢？我们来直接在上一次的代码上修改。

这个网络结构是一层一层的叠加起来的，nn库里有一个类型叫做Sequential序列，正好适合我们。这个Sequential是一个容器类，我们可以在它里面添加一些基本的模块。

model = nn.Sequential()

第一个我们要添加的是输入节点和第一个隐藏层的连接，它是一个Linear线性的类型，它的输入是1个节点，输出是3个节点。

model:add(nn.Linear(1,3))

然后我们在他后面添加一个Sigmoid层，它的节点个数会自动和前一层的输出个数保持一致。

model:add(nn.Sigmoid())

接下来我们添加第一和第二隐藏层中间的线性连接，输入是3，输出也是3。

model:add(nn.Linear(3,3))

再添加一个Sigmoid层。

model:add(nn.Sigmoid())

最后是第二隐藏层和输出节点之间的线性连接，输入是3，输出是1。

model:add(nn.Linear(3,1))

所以完整的建立模型的代码看起来是这样的

model = nn.Sequential()
model:add(nn.Linear(1,3))
model:add(nn.Sigmoid())
model:add(nn.Linear(3,3))
model:add(nn.Sigmoid())
model:add(nn.Linear(3,1))

好，理论上讲我们已经改造完了网络，可以开始训练了。我们运行一下，看一下结果。我们会很意外的发现这个结果还不如我们上一次的结果。

其实这里面存在两个问题：

一个是我们的训练数据，输入的月份取值范围从1到10，输出的价格取值范围是几万。这样开始训练的时候后面几层的梯度会受到输出值的影响，变得非常大，迅速的把前面几层的参数推到一个很大的数值。而Sigmoid函数在远离零点的位置几乎梯度为零，所以就一直固定在一个位置不动了。

解决的方法是把输入和输出的取值范围调整到合适的区间，我这里把输入除以10，输出除以50000。预测时再把50000乘回去。在代码里面体现，就是在开头和结尾加两个辅助层，nn.MulConstant，这种类型的模块是对网络中的每个元素乘上一个常数。在输入进入之前先乘以0.1，在输入之后乘以50000。

这样一来，建立模型的代码就变成了这样：

model = nn.Sequential()
model:add(nn.MulConstant(0.1)) --在输入进入之前先乘以0.1
model:add(nn.Linear(1,3))
model:add(nn.Sigmoid())
model:add(nn.Linear(3,3))
model:add(nn.Sigmoid())
model:add(nn.Linear(3,1))
model:add(nn.MulConstant(50000)) --在输入之后乘以50000

数据预处理问题现在解决了，还有一个问题是训练的速度很慢。因为我们现在的优化方法用的是最原始梯度下降法。

其实Torch已经给我们提供了各种先进的优化算法，都放在optim这个库里。我们在文件的头部添加包含optim库：

require 'optim'

另外，还需要把model里面的参数找出来方便随时调用。

w, dl_dw = model:getParameters()

w是model里面所有可调参数的集合，dl_dw是每个参数对loss的偏导数。需要注意的是这里的w和dl_dw都相当于C++里面的“引用”，一旦你对他们进行了操作，模型里的参数也会跟着改变。

优化函数的调用方法有一点特殊，需要你先提供一个目标函数，这个函数相当于C++里的回调函数，他的输入是一组网络权重参数w，输出有两个，第一个是网络使用参数w时，其输出结果与实际结果之间的差别，也可以叫loss损失，另一个是w中每个参数对于loss的偏导数。

feval = function(w_new)
   if w ~= w_new then w:copy(w_new) end
   dl_dw:zero()

   price_predict = model:forward(month_train)
   loss = criterion:forward(price_predict, price_train)
   model:backward(month_train, criterion:backward(price_predict, price_train))
   return loss, dl_dw
end

这个回调函数可以参照这个例子来写，同样是“例行公事”，调用一下反向传播的算法。

有了这个目标函数，优化迭代的过程就简单多了。只需要一句optim.rprop(feval, w, params)。 rprop是一种改进的梯度下降法，它只看梯度的方向，不管大小，只要方向不变，它会无限的增大步长，所以他速度非常快。迭代的代码如下：

params = {
   learningRate = 1e-2
}

for i=1,3000 do
   optim.rprop(feval, w, params)

   if i%10==0 then
      gnuplot.plot({month, price}, {month_train:reshape(10), price_predict:reshape(10)})
   end
end

其中每10次迭代会把结果用gnuplot画出来。

我们来运行一下。

在命令行键入

th mlp.lua

看一下结果，这次的结果看起来就好多了。绿线（预测值）几乎和蓝线（实际值）重合在一起了。

下一节，我们将介绍如何用卷积神经网络识别MNIST手写数字图像。

本节的完整代码：

require 'torch'
require 'nn'
require 'optim'
require 'gnuplot'

month = torch.range(1,10)
price = torch.Tensor{28993,29110,29436,30791,33384,36762,39900,39972,40230,40146}

model = nn.Sequential()
model:add(nn.MulConstant(0.1))
model:add(nn.Linear(1,3))
model:add(nn.Sigmoid())
model:add(nn.Linear(3,3))
model:add(nn.Sigmoid())
model:add(nn.Linear(3,1))
model:add(nn.MulConstant(50000))
criterion = nn.MSECriterion()

month_train = month:reshape(10,1)
price_train = price:reshape(10,1)

gnuplot.figure()

w, dl_dw = model:getParameters()

feval = function(w_new)
   if w ~= w_new then w:copy(w_new) end
    dl_dw:zero()

    price_predict = model:forward(month_train)
    loss = criterion:forward(price_predict, price_train)
    model:backward(month_train, criterion:backward(price_predict, price_train))
    return loss, dl_dw
end
    
params = {
   learningRate = 1e-2
}

for i=1,3000 do
   optim.rprop(feval, w, params)

   if i%10==0 then
      gnuplot.plot({month, price}, {month_train:reshape(10), price_predict:reshape(10)})
   end
end

month_predict = torch.range(1,12)
local price_predict = model:forward(month_predict:reshape(12,1))
print(price_predict)

gnuplot.pngfigure('plot.png')
gnuplot.plot({month, price}, {month_predict, price_predict})
gnuplot.plotflush()