浅谈Attention及Transformer网络

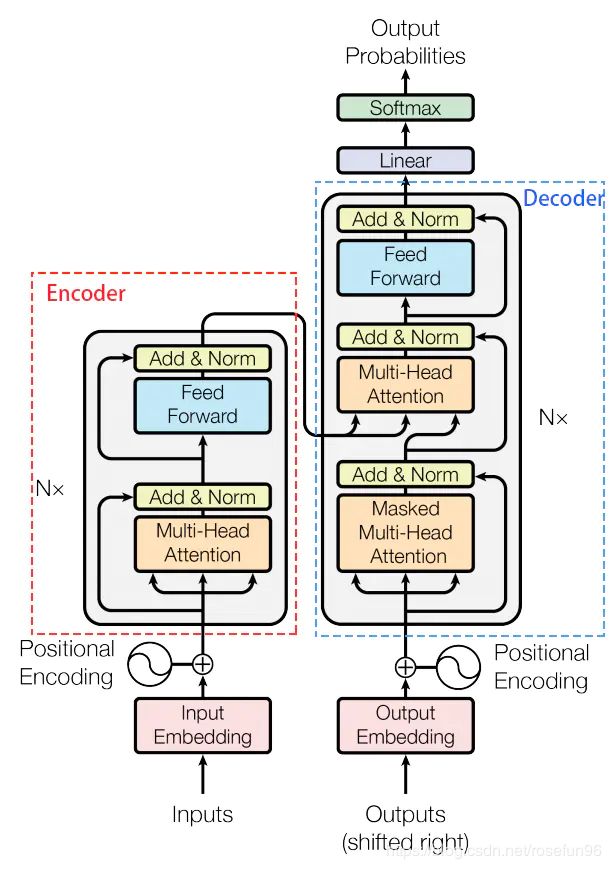
1. Transformer 模型结构

处理自然语言序列的模型有 rnn， cnn（textcnn），但是现在介绍一种新的模型，transformer。与RNN不同的是，Transformer直接把一句话当做一个矩阵进行处理，要知道，RNN是把每一个字的Embedding Vector输入进行，隐层节点的信息传递来完成编码的工作。简而言之，Transformer 直接粗暴（后面Attention也就是矩阵的内积运算等）。

Transformer模型中采用了 encoer-decoder 架构论文中encoder层由6个encoder堆叠在一起，decoder层也一样。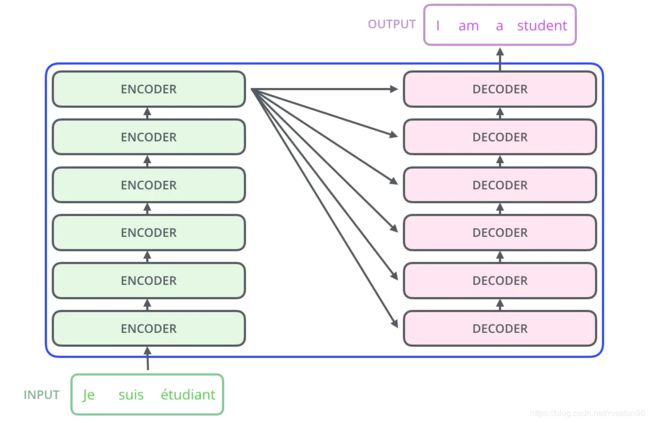

Attention 的编码，把一个输入序列$(x_1,...,x_n)$表示为连续序列$\mathbf{z}=(z_1,...,z_n)$.给定$\mathbf{z}$, 解码生成一个输出序列 $(y_1,...,y_m)$. 模型每一步都是自回归的（？），即假设之前生成的结果都是作为生成下一个符号的额外输入。
TransFormer 模型使用堆叠的自注意力
（self-attention）、逐点（point-wise）、全连接层（fully connected layers）.

Transformer的内部结构（图中N指数量）：

堆叠的编码和解码
编码：编码器由 N=6 个相同的层堆叠成，每层有两个减层（sub-layers）和标准化层。
解码： 有6个相同层堆叠而成，此外，在解码堆叠中，增加自注意力减层，防止 位置出现偏差。

2. 子层Attention

NLP领域中，Attention网络基本成为了标配，是Seq2Seq的创新。Attention网络是为了解决编码器-解码器结构存在的长输入序列问题。
Attention功能可以被描述为将查询和一组键值对映射到输出，其中查询，键，值和输出都是向量。输出可以通过对查血的值加权来计算。

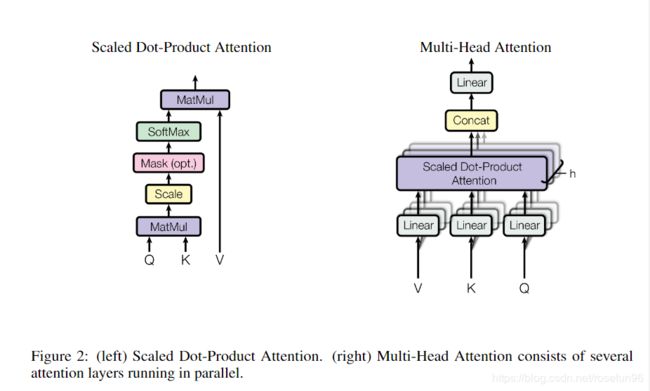
2.1 压缩的点乘注意力机制

输入：查询（query）、键（维度$d_k$）、值（维度 $d_v$）.
查询矩阵Q、键矩阵K、值矩阵V
输出：
$$Attention(Q,K,V)=softmax(\frac{Q{K}^T}{\sqrt{(d_k)}})V$$

Attention与RNN/CNN不同，在于Attention，直接将$x_t$与原来的每个词进行比较，最后算出$y_t$;即
$$y_t=f(x_t,K,V)$$

其中，K,V为另外一个序列或矩阵；如果A=B=X,那么称为 Self Attention, 即上上式子中Q，K， V 都一样，意思就是句子对句子自己进行Attention 来查找句子中词之间的关系。

举例：

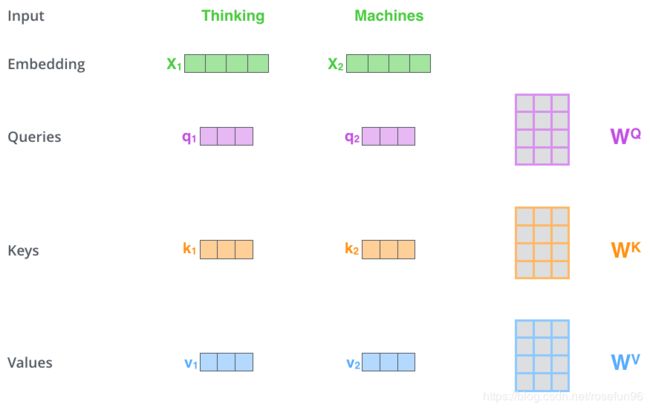
embedding在进入到Attention之前，有3个分叉，那表示说从1个向量，变成了3个向量Q,K,V，它是通过定义一个$W^Q$矩阵（这个矩阵随机初始化，通过前向反馈网络训练得到），将embedding和$W^Q$矩阵做乘法，得到查询向量$q$，假设输入embedding是512维，在上图中我们用4个小方格表示，输出的查询向量是64维，上图中用3个小方格以示不同。然后类似地，定义$W^K$和$W^V$矩阵，将embedding和$W^K$做矩阵乘法，得到键向量k；将embeding和$W^V$做矩阵乘法，得到值向量$v$。对每一个embedding做同样的操作，那么每个输入就得到了3个向量，查询向量，键向量和值向量。需要注意的是，查询向量和键向量要有相同的维度，值向量的维度可以相同，也可以不同，但一般也是相同的。

至于将获得的Q,K,V矩阵具体操作，总的来说，就是以下这幅图。

获得的Z和目标值进行比较，获得的损失反向传播，优化的参数是，$W^Q,W^K,W^V$.

2.2 Multi-Head Attention

$$MultiHead(Q,K,V)=Concat(hea{d}_1,...,hea{d}_h)W^O$$

多头注意力机制，只是多做几次同样的事，然后把结果拼接。tranformer是使用了8组Attention，所以最后得到的结果是8个矩阵。

Attention本质

本质上Attention机制是对Source中元素的Value值进行加权求和，而Query和Key用来计算对应Value的权重系数。

masked mutil-head attetion
mask 表示掩码，它对某些值进行掩盖，使其在参数更新时不产生效果。

两种masked:
padding mask
因为每个批次输入序列长度是不一样的也就是说，我们要对输入序列进行对齐。具体来说，就是给在较短的序列后面填充 0。
然后，把这些填充的位置的值加上一个非常大的负数(负无穷)，这样的话，经过 softmax，这些位置的概率就会接近0！
padding mask 实际上是一个张量，每个值都是一个Boolean，值为 false 的地方就是我们要进行处理的地方。

Sequence mask
sequence mask 是为了使得 decoder 不能看见未来的信息。也就是对于一个序列，在 time_step 为 t 的时刻，我们的解码输出应该只能依赖于 t 时刻之前的输出，而不能依赖 t 之后的输出。因此我们需要想一个办法，把 t 之后的信息给隐藏起来。
方法：产生一个下三角矩阵，把这个矩阵作用在每一个序列上。

3. Position Embedding

Position Embedding,将每个位置编号，每个编号对应一个向量，这样，Attention可以分辨出不同位置的词了。

Position Embedding:
$$\{\begin{array}{lr}P{E}_{2i}(p)=sin(p/10000^{2i/d_{pos}}),& \\ P{E}_{2i+1}(p)=cos(p/10000^{2i/d_{pos}})& \end{array}$$

p,代表位置； i,代表维度；
使用这个公式，在于这个能更好表示相对位置。
由
$$sin(\alpha +\beta )=sin\alpha cos\beta +sin\beta cos\alpha$$

$$cos(\alpha +\beta )=cos\alpha cos\beta -sin\alpha sin\beta$$

位置可以由两个位置之间的线性变换得到。
在偶数位置，使用正弦编码，在奇数位置，使用余弦编码。

4. 子层：前馈网络Position-wise Feed Forward Networks

Encoder中和Decoder中经过Attention之后输出的n个向量（这里n是词的个数）都分别的输入到一个全连接层中，完成一个逐个位置的前馈网络。

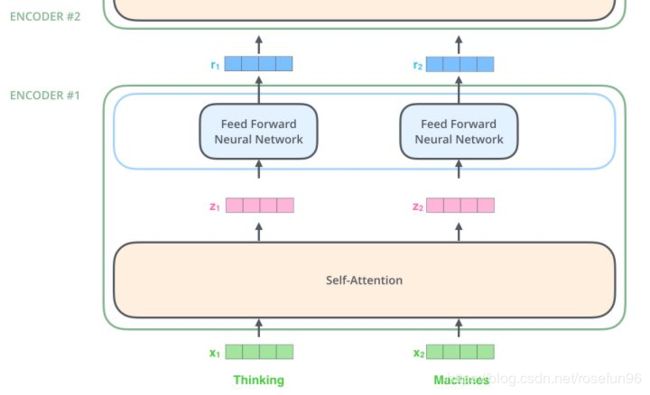
5. Add & Norm

Transformer中每一个Self Attention层与FFN层后面都会连一个Add & Norm层。在Attention和前馈网络两个sublayer后面都接残差连接，然后进行Layer Normalization.

Add&Norm在sublayer后面都接残差连接，然后进行Layer Normalization。因此，Attention和前馈网络的输出经过Add&Norm变成了：
$$\text{L}ayerNorm(x+\text{ Sublayer }(x))$$

Add 是一个残差网络，残差结构能够很好的消除层数加深所带来的信息损失问题。

Normalization有很多种，但是它们都有一个共同的目的，那就是把输入转化成均值为0方差为1的数据。我们在把数据送入激活函数之前进行normalization（归一化），因为我们不希望输入数据落在激活函数的饱和区。

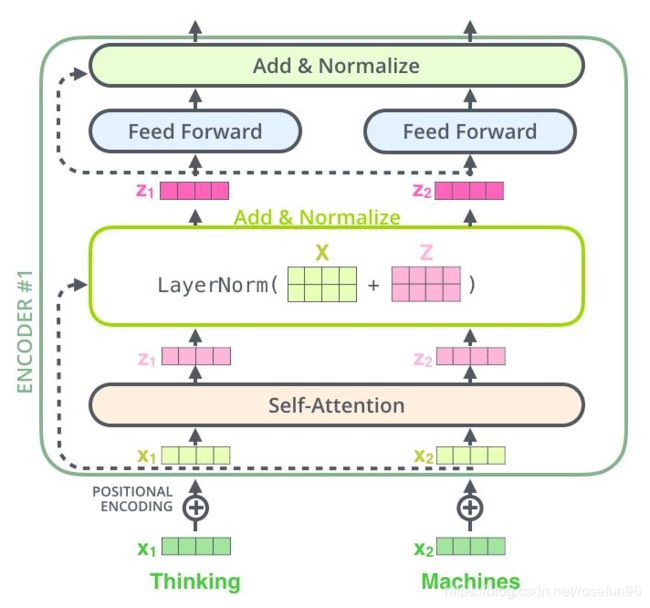
LN 是在每一个样本上计算均值和方差：

6. Linear+Softmax输出

在结尾再添加一个全连接层和softmax层，假如我们的词典是1w个词，那最终softmax会输入1w个词的概率，概率值最大的对应的词就是我们最终的结果。
Encoder是把整个句子作为输入，编码好了。但Decoder是逐个单词来预测的。

7. 实践

import numpy as np 
encoder = np.transpose([[3,12,45], [59,2,5], [1,43,5], [4,3,45.3]])
decoder = np.array([0.5, 0.1, 2])

#Score Matrix
def score(encoder, decoder):
    return np.dot(np.transpose(encoder),decoder)

scoreMatrix = score(encoder, decoder)

#softmax score matrix
def softmax(x):
#    x = np.array(x, dtype = np.float128)
    print(np.exp(x))
    print(np.sum(np.exp(x)))
    return np.exp(x)/np.sum(np.exp(x), axis = 0)
scoreSoftmax = softmax(scoreMatrix)

#multiply with encoder matrix
def multiply(x, weight):
    return np.multiply(x, weight)

weightEncoder = multiply(encoder, scoreSoftmax)

#get Attention Vector
def attentionVec(x):
    return np.sum(x, axis = 1)
att_vec = attentionVec(weightEncoder)

8. 总结

Q: Transformer相比于RNN/LSTM，有什么优势？
A：RNN系列的模型，并行计算能力很差。RNN并行计算的问题就出在这里，因为 T 时刻的计算依赖 T-1 时刻的隐层计算结果，而 T-1 时刻的计算依赖 T-2 时刻的隐层计算结果，如此下去就形成了所谓的序列依赖关系。

Q:为什么说Transformer可以代替seq2seq？
A:
seq2seq缺点: seq2seq最大的问题在于将Encoder端的所有信息压缩到一个固定长度的向量中，并将其作为Decoder端首个隐藏状态的输入，来预测Decoder端第一个单词(token)的隐藏状态。在输入序列比较长的时候，这样做显然会损失Encoder端的很多信息，而且Decoder端不能够关注到其想要关注的信息。

Transformer优点：transformer不但对seq2seq模型这两点缺点有了实质性的改进(多头交互式attention模块)，而且还引入了self-attention模块，让源序列和目标序列首先“自关联”起来，这样的话，源序列和目标序列自身的embedding表示所蕴含的信息更加丰富，而且后续的FFN层也增强了模型的表达能力，并且Transformer 并行计算的能力 是远远超过seq2seq系列的模型，因此我认为这是transformer优于seq2seq模型的地方。

---

reference:

1. 论文 Attention is all you need;
2. bojone Attentionn;
3. blog RNN 中的Attention;
4. kaggle attention ;
5. 公众号大数据文摘 transformer介绍；
6. 英文blog，非常详细，5是其译文；
7. 知乎 Transformer Pytorch实践；
8. 深度学习中的注意力机制(2017版);
9. 一文看懂 Attention（本质原理+3大优点+5大类型）；
10. zhihu Transformer结构及其应用详解–GPT、BERT、MT-DNN、GPT-2 ；
11. BERT代码实现及解读;
12. 作者：mantch 来源：掘金;