什么是群环域具体可以看http://sparkandshine.net/algebraic-structure-primer-group-ring-field-vector-space/这篇博文。
1.初等代数 -> 抽象代数
1.1 数 -> 集合
集合在朴素集合论(naive set theory)和公理化集合论(axiomatic set theory)的定义是不一样的,前者指由一些元素组成;后者指具有某种特定性质事物的总体。
1.2 + ->二元运算
加号+被抽象为二元运算*(binary operation),对两个元素作二元运算,得到的新元素仍然属于该集合,这叫封闭性(closure)。实际上,加减乘除都叫二元运算(二元指的是两个操作数)。
1.3 0/1 单位元
0和1被抽象成单位元(identity elements),0为加法单位元,1为乘法单位元。单位元是集合的一个特殊元素(跟二元运算有关),满足单位元与其他元素相结合时,不改变该元素,即满足a ∗ e = a 与 e ∗ a = a。可见,单位元取决于元素与二元运算,如矩阵的加法单位元是零矩阵,矩阵的乘法单位元是单位矩阵。值得注意的是,有些集合不存在单位元,如正整数集合(the set of positive natural numbers)没有加法单位元(no identity element for addition)。
1.4 负数 -> 逆元素
负数推广到逆元素(inverse element),对于加法,a的逆元素是-a;对于乘法,a的逆元素是倒数a−1。直观地说,逆元可以撤销操作,如加了一个数a,再加上该数的逆元-a(相当于撤消操作),结果还是一样。
1.5 结合律
结合律(Associative property)是某些二元运算的性质,有些二元运算没有结合律(如减法、除法、八元数)。
1.6 交换律
交换律(Commutative property),改变二元运算符两边的元素不影响结果。并不是所有二次元运算都满足交换律(如矩阵的乘法)。
2. Group Like
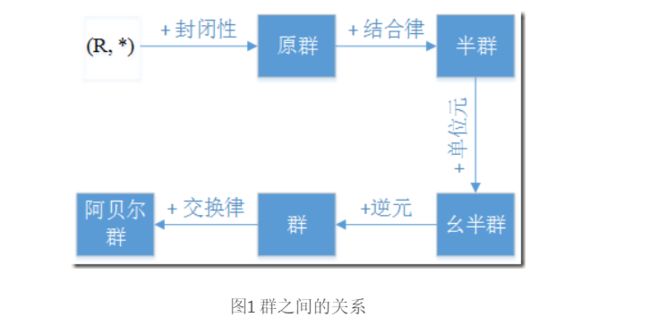
代数结构(R, *),二元运算根据封闭性、单位元、逆元、结合律、交换律,可以归纳成不同的群。本节介绍的group-like,从最不严格到严格(依次添加限制条件),其关系图如下:
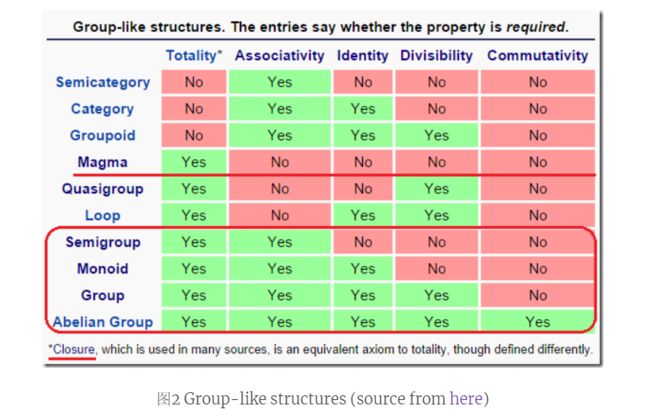
维基百科有一张表,给出更详细的group-like间的关系,如下:
2.1 原群
原群(magma)是一种基本的代数结构,只要满足两元素作二元运算得到新元素仍属于该集合,即封闭性。
2.2 半群
半群(Semigroup),满足结合律(associative property)的代数结构。V=
2.3 幺半群
幺半群(monoid)在半群的基础上,还需要满足有一个单位元。
2.4 群
群(group)是两个元素作二元运算得到的一个新元素,需要满足群公理(group axioms),即:
- 封闭性:a ∗ b is another element in the set
- 结合律:(a ∗ b) ∗ c = a ∗ (b ∗ c)
- 单位元:a ∗ e = a and e ∗ a = a
- 逆 元:加法的逆元为-a,乘法的逆元为倒数1/a,… (对于所有元素)
如整数集合,二次元运算为加法就是一个群(封闭性是显然的,加法满足结合律,单位元为0,逆元取相反数-a)。

2.5 阿贝尔群(交换群)
阿贝尔群(Abelian Group)在群的基础上,还需满足交换律。如整数集合和加法运算,(Z,+),是一个阿贝尔群。
2.6 循环群
3. 环论
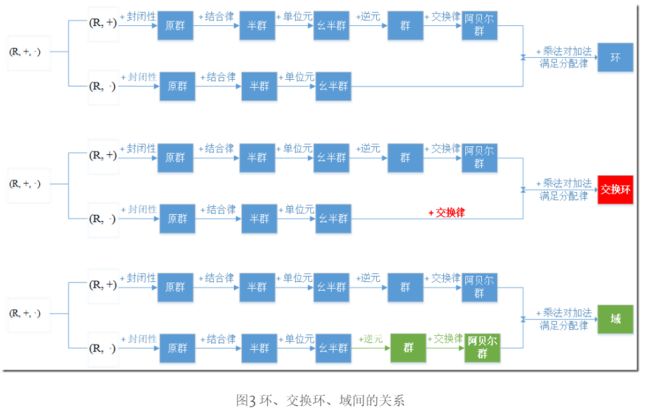
环在交换群基础上,进一步限制条件。环、交换环、域间的关系如下:
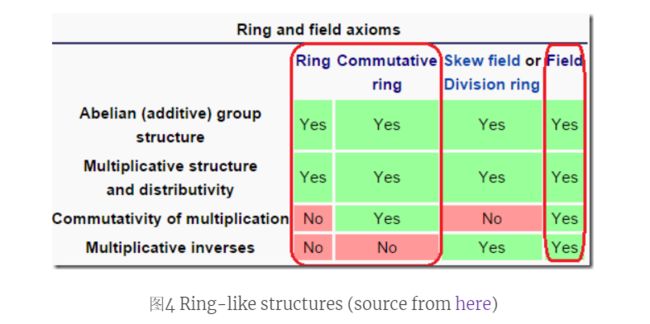
维基百科有一张表从不同角度呈现这三者的关系,如下
3.1 环
环(ring)在阿贝尔群(也叫交换群)的基础上,添加一种二元运算·(虽叫乘法,但不同于初等代数的乘法)。一个代数结构是环(R, +, ·),
需要满足环公理(ring axioms),如(Z,+, ⋅)。环公理如下:


3.2 交换环
3.3 整环
整环(integral domain)在交换环的基础上,并满足没有零因子(如此,集合内任意两个元素乘积均不等于0)。

4. 域
域(Field)在交换环的基础上,还增加了二元运算除法,要求元素(除零以外)可以作除法运算,即每个非零的元素都要有乘法逆元。由此可见,域是一种可以进行加减乘除(除0以外)的代数结构,是数域与四则运算的推广。整数集合,不存在乘法逆元(1/3不是整数),所以整数集合不是域。有理数、实数、复数可以形成域,分别叫有理数域、实数域、复数域。








