LeetCode刷题：62. Unique Paths 和 63. Unique Paths II

LeetCode刷题：62. Unique Paths

62. Unique Paths 原题链接：https://leetcode.com/problems/unique-paths/description/
63. Unique Paths II 原题链接：https://leetcode.com/problems/unique-paths-ii/description/

62. Unique Paths

A robot is located at the top-left corner of a m x n grid (marked ‘Start’ in the diagram below).

The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked ‘Finish’ in the diagram below).

How many possible unique paths are there?

Above is a 3 x 7 grid. How many possible unique paths are there?

Note: m and n will be at most 100.

这个题目的意思是给定了一个M*N的格子，一个机器人从左上角需要移动到右下角。每次移动时只能向右或者向下移动。问机器人从标记为START的位置移动到标记为Finish的位置，一共有多少条可能不同的路径？

图例给出的是3*7的方法。

注意：M和N的最大值为100。

问题分析：

这个问题可以使用DP算法来求解。

如图所示：

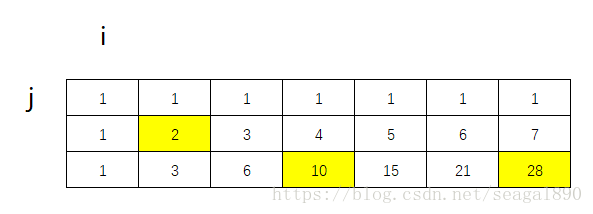
建立一个DP数组 dp[i][j]，数组元素的值代表从上一步移动到下一步的路径数量。
当 i=0，j=0时，即左上角的格子初始值为1。
从左上角向右移动，从 $array[0][0]$移动到 $array[0][1]$，只有一种路径，所以 $dp[0][1]$的值为1。
同理，从左上角向下移动，从 $array[0][0]$移动到 $array[1][0]$，只有一种路径，所以 $dp[1][0]$的值为1。

对于单元格 $array[1][1]$而言，可以从 上方单元格$array[0][1]$ 移动过来，也可以从其左方的单元格 $array[1][0]$ 移动过来，所以 $dp[1][1] =dp[0][1] + dp[1][0] $，这样移动到 单元格 $array[1][1]$ 的路径就有 1+1 = 2 条。

依次类推，可以建立状态方程。

建立状态转移方程：
对于第一行：$dp[0][i]=1$
对于第一列：$dp[j][0]=1$
对于一般情况：$dp[i][j]=dp[i-1][j]+dp[i][j-1]$

算法设计：

package com.bean.algorithmbasic;

public class UniquePathsDemo {
	
	/*
	 * ｍ和ｎ最大不超100。
	 * */

	public static int uniquePaths(int m, int n) {
		int[][] dp  = new int[m][n];
		// 第一列的解
		for (int i = 0; i < m; i++) {
			dp[i][0] = 1;
		}
		// 第一行的解
		for (int i = 1; i < n; i++) {
			dp[0][i] = 1;
		}
		// 其它位置的解
		for (int i = 1; i < m; i++) {
			for (int j = 1; j < n; j++) {
			    //动态规划核心：状态转移方程
				dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
			}
		}
		// 所求的解
		return dp[m - 1][n - 1];
	}

	public static void main(String[] args) {
		// TODO Auto-generated method stub
		int result = uniquePaths(3, 7);
		System.out.println("RESULT IS: " + result);
	}

}

输出结果为：

RESULT IS: 28

LeetCode上提交的代码，AC后的结果。

class Solution {
    public int uniquePaths(int m, int n) {
        int[][] dp  = new int[m][n];
		// 第一列的解
		for (int i = 0; i < m; i++) {
			dp[i][0] = 1;
		}
		// 第一行的解
		for (int i = 1; i < n; i++) {
			dp[0][i] = 1;
		}
		// 其它位置的解
		for (int i = 1; i < m; i++) {
			for (int j = 1; j < n; j++) {
				dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
			}
		}
		// 所求的解
		return dp[m - 1][n - 1];
    }
}

63. Unique Paths II

Follow up for “Unique Paths”:

Now consider if some obstacles are added to the grids. How many unique paths would there be?

An obstacle and empty space is marked as 1 and 0 respectively in the grid.

For example,
There is one obstacle in the middle of a 3x3 grid as illustrated below.

[
[0,0,0],
[0,1,0],
[0,0,0]
]
The total number of unique paths is 2.

Note: m and n will be at most 100.

63题和62题类似，不同的是设置了 obstacle，当遇到obstacle时，此路不同。
解题思路仍然是使用DP动态规划算法。无非对于dp数组元素，在obstacle位置将器值置位0即可。
需要增加一些判断条件。

算法设计

	public static int uniquePathsWithObstacles(int[][] obstacleGrid) {
		//获取被处理数组的维度，m行n列
		int m = obstacleGrid.length;
		int n = obstacleGrid[0].length;
		if(m==0 || n==0) return 0; 
		//计算时间，即如果左上角的元素值为1，直接返回0。
		if(obstacleGrid[0][0]==1) return 0;
		
		//DP（Dynamic Programming）数组为s，s与被处理的二维数组具有相同的行和列数
		int[][] dp = new int[m][n];
		//用dp[i][j]表示路径数
		//当方格的左上角和右下角（第一个元素值为1时和最后一个元素值为1时，路径都为0）
		dp[0][0] = obstacleGrid[0][0] == 0 ? 1 : 0;
		if (dp[0][0] == 0)
			return 0;
		for (int i = 0; i < m; i++) {
			for (int j = 0; j < n; j++) {
				if (obstacleGrid[i][j] == 1)
					//如果是路障，则dp[i][j]=0
					dp[i][j] = 0;
				else if (i == 0) {
					if (j > 0)
						dp[i][j] = dp[i][j - 1];
				} else if (j == 0) {
					if (i > 0)
						dp[i][j] = dp[i - 1][j];
				} else
					//如果不是路障，则状态方程为dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
					dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
			}
		}
		return dp[m - 1][n - 1];
	}

LeetCode上提交了一个版本的代码，AC了。

class Solution {
    public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        // Empty case
		if (obstacleGrid.length == 0)
			return 0;

		int rows = obstacleGrid.length;
		int cols = obstacleGrid[0].length;

		for (int i = 0; i < rows; i++) {
			for (int j = 0; j < cols; j++) {
				if (obstacleGrid[i][j] == 1)
					obstacleGrid[i][j] = 0;
				else if (i == 0 && j == 0)
					obstacleGrid[i][j] = 1;
				else if (i == 0)
					obstacleGrid[i][j] = obstacleGrid[i][j - 1] * 1;// For row 0, if there are no paths to left cell,
																	// then its 0,else 1
				else if (j == 0)
					obstacleGrid[i][j] = obstacleGrid[i - 1][j] * 1;// For col 0, if there are no paths to upper cell,
																	// then its 0,else 1
				else
					obstacleGrid[i][j] = obstacleGrid[i - 1][j] + obstacleGrid[i][j - 1];
			}
		}

		return obstacleGrid[rows - 1][cols - 1];
    }
}

（完）