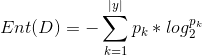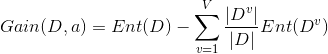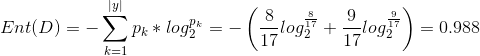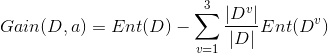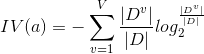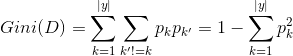简述决策树,随机森林和XGBOOST之间的关系
本文主要讲解:决策树,随机森林和xgboost,附带讲解AdaBoost和GBDT
1.决策树
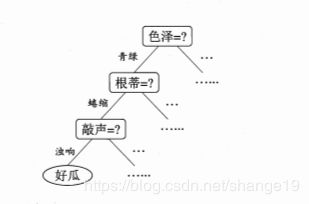
这些算法都依赖于决策树或者决策树的各种魔改版,所以决策树是一定要掌握清楚的。决策树是一种常见的机器学习算法,决策树的目的是构造一种模型,使之能够从样本数据的特征属性中,通过学习简单的决策规则——IF THEN规则,从而预测目标变量的值。以西瓜的例子来说,给定类似色泽,根蒂以及敲声等特征,怎么判断一个西瓜是不是好西瓜。
通过一系列的判定,最终得到【色泽=青绿, 根蒂=蜷缩,敲声=浊响】的西瓜是好瓜。
一般来说,一棵决策树包含一个根节点,若干个内部节点和若干个叶节点。其中,叶节点对应与决策结果,其他每个节点则对应一个属性测试。这里最重要的是如何选择最优属性进行划分?为什么色泽是第一个属性而不是根蒂呢?这里引出了各种划分选择。
1.1 信息增益(ID3算法)
目前的决策树算法主要有:ID3, ID4.5和CART。在ID3中,按照信息增益作为准则来选取划分属性。我们希望决策树的分支节点包含的样本尽可能属于同一类别,即结点的‘纯度’越来越高。
‘信息熵’是度量样本集合纯度最常用的一种指标。
假定当前样本集合D中第k类样本所占比例为![]() (k = 1, 2, .....
(k = 1, 2, ..... ![]() ),D的信息熵定义为:
),D的信息熵定义为:
其中,![]() 为D的样本类别总类。如西瓜例子中标签为好瓜和坏瓜,则
为D的样本类别总类。如西瓜例子中标签为好瓜和坏瓜,则![]() 。
。
信息熵是一个节点的固有性质,对于确定的数据集来说,这是一个定值。
在定义了信息熵之后,对信息增益进行定义,假设选取属性a有V个取值(即能被分成v份),![]() 。按照决策树的规则,D将被划分为V个不同的节点数据集。考虑到不同节点包含样本数不同,给分支赋予相对于的权重,即样本越多的分支权重越大。于是,我们可以算出用属性a对样本集D进行划分得到的‘信息增益’:
。按照决策树的规则,D将被划分为V个不同的节点数据集。考虑到不同节点包含样本数不同,给分支赋予相对于的权重,即样本越多的分支权重越大。于是,我们可以算出用属性a对样本集D进行划分得到的‘信息增益’:
<1>信息增益越大,则用属性a来划分所获得的纯度越大.
<2>Ent(D)是信息熵,是这个数据集的固有性质,为一个定值
<3>![]() 表示分支节点所占的比例大小,调整权重,显然数据集越大的分支节点权重越高。
表示分支节点所占的比例大小,调整权重,显然数据集越大的分支节点权重越高。
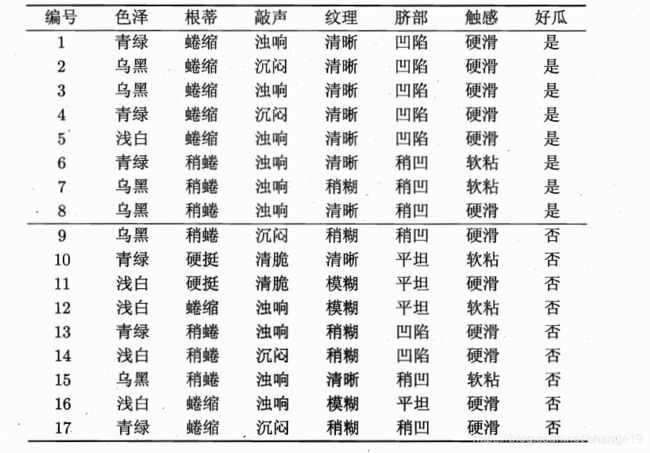
让我们来计算一个例子,还是以西瓜为例:
西瓜数据集中,总共17个样本。很显然,![]() 。其中正例有8个,反例有9个。根据上面的公式,可得根节点的信息熵为:
。其中正例有8个,反例有9个。根据上面的公式,可得根节点的信息熵为:
然后,我们要按照当前属性进行划分。以色泽为例,有三种取值:青绿,乌黑和浅白。记划分后的三个子集D1{色泽=青绿},D2{色泽=乌黑}, D3{色泽=浅白}。在D1中,有6个样本,其中3个正例,3个反例;在D2中,有6个样本,其中4个正例,2个反例;在D3中,有5个样本,其中1个正例,4个反例。按照‘色泽’划分后的三个分支节点的信息熵为:
于是,可以得到信息增益为(a=色泽):
所以,按照色泽属性进行划分的信息增益为0.109。
其中属性的信息增益为:G(D,根蒂)=0.143, G(D,敲声)=0.141, G(D,纹理)=0.381, G(D,脐部)=0.289, G(D,触感)=0.006。
显然,‘纹理’的信息增益最大,于是选它作为划分属性。以此类推,直至当前节点全为同一类别。
但是,在上面的表中,我们忽略了一个特征,那就是编号,如果按照编号进行划分,那么信息增益为0.998。但是这样的划分没有任何意义。这就是信息增益准则的缺点:偏爱那些取值数目较多的属性。下面解释信息增益率准则。
1.2 信息增益率准则(C4.5算法)
为了减少信息增益准则对取值数目较多的属性有所偏好的缺点,采用增益率来选择最优划分属性。增益率定义为:
<1> ![]() 是属性a的‘固定值’。属性a的取值数目越多(v越大),则
是属性a的‘固定值’。属性a的取值数目越多(v越大),则![]() 越大。如IV(编号)=17,IV(色泽)=1.580。
越大。如IV(编号)=17,IV(色泽)=1.580。
<2>C4.5相比较于ID3,就是乘以了一个系数来限制偏好取值数目多的属性。
<3>在C4.5算法中,并不俗直接选择增益率最大的属性,而是先从候选属性中找出信息增益高于平均水平的属性,再从中选择信息率最高的属性。
1.3 基尼指数(CART决策树)
在CART决策树中,使用基尼指数来选择属性,首先定义数据集D的基尼值:
形象的说,基尼值代表了从D中随机选择两个样本,其类别不一致的概率。有了基尼值后,可以在此基础上定义基尼指数:
于是,我们选择使得划分后基尼指数最小的属性作为最优划分属性。
主要的三种决策树算法已经讲解完了。还有一些其他的处理手段来优化决策树,比如:剪枝、连续值与缺失值处理、多变量决策树等等。就不一一介绍了。
1.4 剪枝
剪枝是应该决策树过拟合的一种重要方法,主要分为以下两种:
预剪枝:该策略就是在对一个节点进行划分前进行估计,如果不能提升决策树泛化精度,就停止划分,将当前节点设置为叶节点。那么怎么测量泛化精度,就是留出一部分训练数据当做测试集,每次划分前比较划分前后的测试集预测精度。
优点:降低了过拟合风险,降低了训练所需的时间。
缺点:预剪枝是一种贪心操作,可能有些划分暂时无法提升精度,但是后续划分可以提升精度。故产生了欠拟合的风险。
后剪枝:该策略是首先正常建立一个决策树,然后对整个决策树进行剪枝。按照决策树的广度优先搜索的反序,依次对内部节点进行剪枝,如果将某以内部节点为根的子树换成一个叶节点,可以提高泛化性能,就进行剪枝。
优先:降低过拟合风险,降低欠拟合风险,决策树效果提升比预剪枝强
缺点:时间开销大得多
2.集成学习
通过集成学习衍生出的树模型算法主要有:随机森林、AdaBoost和XgBoost。
首先介绍一下集成学习,集成学习通过将多个弱学习器进行结合,对结果进行投票,通常可以获得比单一学习器更优越的性能。
如果基学习器互相独立,随着学习器数目的增大。错误率将会以指数级下降,最终趋近于0(基学习器应优于随即猜测的学习器,利于二分类问题基学习器精度应该高于50%)。这里的数学公式不推导,感兴趣的查阅周志华的西瓜书。
但是,面对同一个问题,个体学习器是训练同一个样本,不可能相互独立!!。也就是说,面对一个问题,我们集成再多的决策树,很有可能达不到我们预期的结果。
所以,目前主要有两大类集成学习方法:
1.Bossting:个体学习器之间存在强依赖关系,串行生成的序列化方法,主要代表Adaboost,GBDT, XgBoost
2.Bagging:个体学习器之间不存在强依赖关系,同时生成的并行方法,主要代表随即森林
2.1 Bagging
我们先介绍bagging,随机森林是bagging中的一个扩展变种。在面对同一个问题,不可能做到‘相互独立’,于是bagging的思想尽可能使个体学习器之间有较大差异。给定一个数据集(N个样本),利用boot strap方法(从N个样本中随机取出M个,M 2.1.1随机森林(Random Forest) 随即森林是bagging中的一个扩展变种,在bagging的基础上,进一步在训练过程中引入随机属性选择。具体来说,bagging是随机选择样本,而随机森林在随机选择样本的基础上,从d个属性中随机选择k个属性。一般情况下,推荐使用 随机森林的优点:简单,容易实现,计算开销小。 从偏差-方差的角度看,Boosting主要关注降低偏差。 个体学习器之间存在强依赖关系,串行生成的序列化方法。这类方法主要机制如下:先从初始训练集中训练一个基学习器,在根据及学习的表现对样本进行调整,基于调整后的样本训练下一个基学习器,反复进行,直至基学习器数目达到事先指定数目T,然后再将这T个基学习器进行加权结合。 2.2.1 AdaBoost 1.AdaBoost改变了训练数据的权值,也就是样本的概率分布,其思想是将关注点放在被错误分类的样本上,减小上一轮被正确分类的样本权值,提高那些被错误分类的样本权值。然后,再根据所采用的一些基本机器学习算法进行学习,比如决策树。 2.AdaBoost采用加权多数表决的方法,加大分类误差率小的弱分类器的权重,减小分类误差率大的弱分类器的权重。这个很好理解,正确率高分得好的弱分类器在强分类器中当然应该有较大的发言权。 在这里简述一下AdaBoost的流程。 对于一个训练集D有m个样本,训练次数T,基学习算法R。 Adaboost流程: 1.初始化权重,第一次所有权重都相同,都为1/m,样本集变为D1 2.for t = 1...T: 3.计算基于t时刻数据集的结果 4.计算此学习器的误差率 5.如果 8.end 这个AdaBoost的输出依赖于所有的基学习器按照权重投票得到的输出。误差率越大的基学习器权重越大。在每轮迭代中,错误的样本会得到更大的权重,正确的样本会得到更小的权重,改变了样本的概率分布。将改变后的样本分布作为下一次的输入。 第五步,实际是判定当前生成的基学习器是否满足基本要求,即优于随即猜测。 具体公式推导可以参考周志华的西瓜书。 2.2.2 GBDT 未完待续![]() 。
。2.2 Boosting
![]()
![]()
![]() ,退出此次循环
,退出此次循环