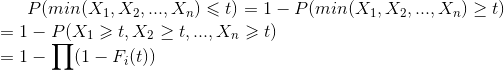概率与统计笔记
这部分数学的基本思想是：
在有上帝视角的时候，知道事件发生的分布，计算某些事件发生的概率，及一些分布的特征。
在没有上帝视角的时候，靠已知事件发生的频率推断事件的分布类型，或者分布的一些特征
1.贝叶斯定理可以根据客观条件看成是对先验概率
的不断修正。
2. 我们现在使用的概率：将样本空间中的事件映射为随机变量表示的值，用一个函数将事件或随机变量映射到(0,1)之间。
3. 伯努利分布：两件事情，映射为0，1. 伯努利分布函数给出每次实验任意一个事件发生的概率。
4. 二项分布，是n重伯努利分布，是进行n次实验某事件发生k次的概率。随机变量为发生次数。
5. 泊松分布，是n趋于无穷大的二项分布，随机变量是在某段时间内某事件发生k次的概率。随机变量是发生次数。
6. 几何分布，是二项分布中某事件发生一次所需要的试验次数为k的概率，随机变量是二项分布中某事件发生一次所需要的试验次数。
7. 负二项分布，是二项分布中事件发生r次所需要试验次数为k的概率。随机变量是试验次数。是r次几何分布的叠加。
8. 指数分布，是泊松分布中两个事件发生间隔时间小于t的概率。随机变量为间隔时间。
9. 正态分布，是对n趋向于无穷大的二项分布的逼近。随机变量是发生的数量。
10. 如果
, 那么可以随之计算出Y的概率密度函数
11.逆随机采样。 因此在python中随机数的生成其实是这样的。随机数应该是服从正态分布的。
,这里令
,根据10,
。那么按照均匀分布得到一个Y，就可以得到一个服从正太分布的X,
12. 多维随机变量的分布。将一个样本空间中的事件的多个特征映射为随机变量。有一个概率函数可以把这多个随机变量映射到（0，1）之间。
13. 边缘的概率质量/密度函数，直观是把质量/密度压到了一维。
14. 条件概率和分布，本质是给出的条件不同，那么得到的分布也不同。条件概率和条件分布同样适用贝叶斯和全概率公式。
15.多维随机变量函数分布的计算：已知X，Y联合分布函数，求XY的随机变量函数分布
Z = X+Y的概率密度是什么：
![F_{X+Y}(Z) = P(X+Y\leq Z)=\iint_{x\leq z-y}p(x,y)dxdy\\=\int_{-\varpi }^{+\varpi }[\int_{-\varpi } ^{z-y}p(x,y)dy]dx](http://img.e-com-net.com/image/info8/a82b57b1a4e54889baf5849ae2411e22.gif)
令
则：
的概率密度
令
商函数数相同求法
极值函数：即X1,X2,...XN最小/大值的概率分布
最大值概率分布
最小值概率分布
16. 大数定律：当实验很多次时，实验得到的值会向真实分布的值靠近。
当统计的数据足够大，那么事情发生的频率无限接近于期望。当你和一个人聊天的次数越多，他的态度代表的数字（随机变量）的算术平均数越接近于他内心真实的态度。
17.中心极限定理：当实验很多次，则这么多次的实验结果加起来服从正态分布。
任何一个样本均值约等于总体均值。
样本均值围绕总体均值呈正态分布。
18. 数理统计与概率区别。
概率是已知样本分布，已经有上帝视角，求现实中事件发生的概率。
统计是不知道分布，不知道参数。从已知数据，比如说重复实验n次，事件发生n次，来对分布和参数进行推断。主要是通过样本的统计量。比如样本均值，样本方差，中位数等。
19，20的样本分布和区间估计知识前提是总体服从正态分布，即只适用于服从于正态分布的总体。
19. 因为每次进行的实验服从的分布和上帝视角的总体分布一定是相同的。那么通过n次实验得到的统计量可能和总体分布有些关系。
如果总体样本服从正态分布：
1）样本均值的分布（有上帝视角）
我们就可以得到统计量的分布。
,这是进行重复n次实验得到的随机变量。
那么它们的样本均值是：
根据大数定理，当n趋向于无穷大时：
即统计量无穷大时与上帝视角均值相同。
那么当n不能为无穷大时呢，
肯定是服从一个分布的。
因为如果我们有上帝视角，知道上帝视角的方差，即总体方差。那么
，
那我们猜想（大概率是对的，因为一切事物上帝视角都是服从正态分布的）
是服从均值为
,方差为
的正太分布。
即：
2）样本方差的分布
如果令
则 
，所以我们认为
要比真实方差小，在这里进行调整，令
，这时
。
根据大数定理，当n趋向于无穷大时，
。当试验次数有限时，
服从什么分布呢？
, 即
服从一个自由度为n-1的卡方分布。（卡方分布不懂）
3）如果上帝视角不知道总体方差是什么，那么如何求的分布。
令
，则这个新的随机变量服从t(n-1)的分布。
4）两个样本方差比例服从的分布
服从F（n-1,m-1）分布
20. 样本对参数的估计分为两种。第一种是点估计，即估计出一个值；第二种是区间估计，即给出一个区间，参数有95%等可能性在这个区间里。这里95%就是置信水平，这个区间就是置信水平为95%的置信区间。就是有100次个样本，这100样本均值构成的区间，参数落在95个区间里。
1. 点估计
包括矩估计和最大似然估计。
矩估计是令样本的统计值和参数进行对应，从而对另外一些参数进行估计。
最大似然估计是找到令发生事件发生的概率最大的参数，从而对参数进行估计。
2. 区间估计。找到一个合适的长度，令100个样本均值组成的区间，有95个可以包含参数。
如果总体样本服从正态分布：
如果参数是期望。那么使用统计值样本均值进行估计。从上帝视角来讲，样本均值服从正态分布
。那么落在
之内的概率为95%。即100个样本均值，概率上有95个的值在那个区间。那么对于这95个值，区间长度为多少才能让参数落在自己区间内。答案是
,即区间应为
,100个这种区间，参数可能落在95个区间内。
21. 假设检验。
假设检验是针对一个东西做两个假设。
和
,找出下该事件的概率分布，如果真实发生的概率落在的拒绝域里，就是发生概率非常小的区间，则拒绝原假设,否则接受原假设。