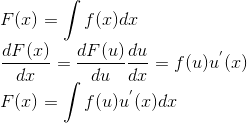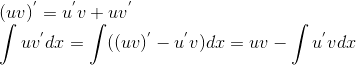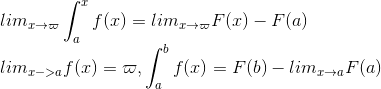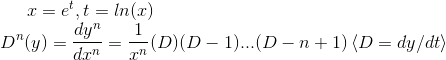单变量微积分笔记
根本思想是在趋向极限的过程中,以直代曲
无穷小的来源和无穷小与极限的关系
1. ![]() 在极限里的意思是不断缩小的观察范围。不断缩小观察范围,如果提高放大倍数,时间还在观察范围内,这就是收敛的极限。
在极限里的意思是不断缩小的观察范围。不断缩小观察范围,如果提高放大倍数,时间还在观察范围内,这就是收敛的极限。
2. 无穷小/大的不是数,而是函数如数列和函数。
3. 无穷大意味着没有极限。
4. 在自变量的同一变化过程中,如果f(x)的极限是无穷大,那么![]() 的极限是无穷小。如果
的极限是无穷小。如果![]() 的极限是无穷小,并且
的极限是无穷小,并且![]() ,那么
,那么![]() 的极限是无穷大
的极限是无穷大
5. 极限的性质分为:唯一,有界,保号。分别描述的是函数在去心邻域内只存在一个极限,在去心邻域内内有界,正负相同。
6. 极限可表示为无穷小的代数![]() , 其中
, 其中![]() 为无穷小。可以看成差值为无穷小。
为无穷小。可以看成差值为无穷小。
7. 无穷小的运算法则:有限个无穷小相加还是无穷小。有界乘于无穷小还是无穷小。
8. 无穷小的分配律:根据6可以推出
9.多项式的极限是分母和分子都化成无穷小的函数。
![]() 形势的极限
形势的极限
11.8中上下分母都为无穷小(一般为三角函数),那么这时用夹逼定理求极限。在![]() 的去心邻域内,
的去心邻域内,![]()
12. 无穷小的比较比较的是哪个接近0的速度更快,从而分出高阶,同阶,低阶,等价。从而可以进行计算。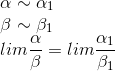
13. 单调有界数列/函数有极限
14. ![]() 单调有界,则有极限,定义其极限为e = 2.74。由夹逼定理可得
单调有界,则有极限,定义其极限为e = 2.74。由夹逼定理可得![]() 的极限也是e。
的极限也是e。
解决连续
15. 连续的定义:如果一个函数在某个邻域内有定义,并且![]() ,则函数在这一点连续。即:
,则函数在这一点连续。即:
![]() 与
与![]() 之间的距离要多小有多小,没有缝隙的黏在一起。
之间的距离要多小有多小,没有缝隙的黏在一起。
解决间断
16. 间断的情况:![]() 在
在![]() 的去心邻域内有定义,
的去心邻域内有定义,
1)![]() 在
在![]() 上有定义,即
上有定义,即![]() 存在
存在
2)![]() 在
在![]() 上有定义,即
上有定义,即![]() 存在,
存在,![]() 不存在
不存在
3)![]() 在
在![]() 上有定义,即
上有定义,即![]() 存在,
存在,![]() 不存在,
不存在,![]()
17.间断可分为两类:第一类:可去间断点和跳跃间断点 左右极限存在
第二类:其他间断点 左右极限不存在
18. 连续的运算:连续函数的四则运算结果也连续。连续函数的初等复合函数也连续。连续函数的反函数也连续。如果运算中有一个函数有间断,则连不连续需要判断。
微分和导数
19. 什么是微分?
微分是对差分的线性近似。差分是把原概念分为无数多份的其中一份。微分和差分都是无穷小。因此可以近似替代。![]()
20. 什么是切线,什么是切线的斜率,怎么计算?
切线是割线的极限,切线斜率是割线斜率的极限
怎么定义微分?什么是可微?
21. 微分函数:将坐标系原点移到![]() 处,该点切线的函数
处,该点切线的函数
![]()
用微分算子完成这一映射
![]()
即:![]()
即可以写成:![]()
![]() 是对
是对![]() 的近似,也是线性映射。
的近似,也是线性映射。
22. 微分定义:函数在魔偶一区间内有定义,![]() 及
及![]() 在此区间内,如果函数增量
在此区间内,如果函数增量![]() 可以表示为
可以表示为![]() (可导),则称
(可导),则称![]() 在
在![]() 是可微的。
是可微的。![]() 叫做函数
叫做函数![]() 在点
在点![]() 相应于自变量增量
相应于自变量增量![]() 的微分(转移坐标系),记作
的微分(转移坐标系),记作![]() (做映射)。即:
(做映射)。即:
![]()
23.由22看出,可导与可微是充分必要关系。
24. 导函数:导函数是定义域各点上的斜率。
25. D算子,表示的是原函数到导函数的映射。算子表示的是函数之间的映射。
![]()
26. 函数的微分
在定义域各点上的微分
![]()
27. 可导一定连续,反过来不一定成立。
28. 反函数的导数是什么?
![]() , 证明可以将f(x)代入。也可以根据反函数与原函数关于y=x对称来证明。
, 证明可以将f(x)代入。也可以根据反函数与原函数关于y=x对称来证明。
29. 什么是隐函数?
隐函数就是不能显示的说y=什么x.
根据函数的定义,x的所有元素都由y 相对应。每一个x对应唯一一个Y.。那么很多在全部定义域内并不符合,只在一个区间内符合函数的定义,我们称作邻域内的隐函数。
30. 最值和极值
在定义区间上大于等于任一点的值称为最值。
在某一去心邻域内大于任意一点称为极值。
如果是极值并且在该点可导,那么这一点的导数为0.
在闭区间的两端的导数如果不相等,在么在这个区间肯定存在一点的导数在这两个点的导数之间。
即,导函数一定满足介值性。
31. 罗尔中值定理
讲的是如果一个函数在开区间可导,闭区间连续,并且在闭区间两端的函数值相等。那么这个区间内一定有一个点的导数为0.
证明分两种情况。第一种情况是这个区间上的函数最大值与最小值相等。则导数在区间上恒为0。第二种情况是最大值和最小值都存在且不相等,那么一定有一个是在两端的。另一个最值则是极值,并且因为在该点可导,根据费尔引理可知,该点导数为0。
32. 微分中值定理(拉格朗日中值定理)
讲的是在一段路程中,一定有一点的速度和平均速度相等。或者是一定有一点的切线与两端连线平行。这个定理是罗尔中值定理的旋转。正如同介值定理是零点定理的平移。![]()
证明时用了一个辅助函数,该函数在两端的值相等且为0,那么根据罗尔中值定理,一定会有一点的导数为0.即可得出拉格朗日中值定理。
可以用这个定理判断函数增减。
33. 柯西中值定理
一个函数的变量x,y都可以用一个函数来表示,那么根据微分中值定理有![]()
证明是用辅助函数证明的。
柯西中值定理 ,微分中值定理,罗尔中值定理之间的关系是这样的:
34. 洛必达定理
洛必达定理是求![]() , 即当
, 即当![]() ,求这时的
,求这时的![]() 。这里用函数变化率的比值来代替。可以用柯西中值定理来证明。
。这里用函数变化率的比值来代替。可以用柯西中值定理来证明。
其他不是零比零形式的可以变换到这种形式求解。
35. 牛顿插值法和泰勒多项式
牛顿插值法和泰勒多项式都是想对一系列数据的映射f(x)的近似。
泰勒多项式是令这n个点等距,并且间隔![]()
那么f(x)可以用泰勒多项式和余项来表示。
![]()
证:
余项可以用来判断函数值的范围
泰勒公式的用途:更容易处理![]() 类型极限或找到一些函数的范围
类型极限或找到一些函数的范围
36. 用导数判断极值点
极值的定义是该点的值大于(小于)去心邻域内所有点的值。
第一种判断方法:根据导数定义,可以证明,极大值点去心邻域内左边的导数大于0,右边点的导数小于0。
第二种判断方法:如果一点导数为0,根据泰勒展开,可以证明,如果该点二阶导数大于0,那么邻域内所有点的值大于该点的值,该点位极小值。同理可证极大值。如果二阶导数为0或不存在,则既不是极小也不是极大值。
37. 用导数判断凹凸性和拐点
曲线方程:![]()
凹的地方是弦在曲线上面。![]()
凸的地方是弦在曲线下面。![]()
如果函数为凹函数,
同理可说明凸函数的情况。
另一种判断凹凸的方式是二阶导数。证明是通过拉格朗日中值定理来证明的。总的来说是二阶导数大于零,曲线在弦的下面,是凹函数。二阶导数小于0,那么弦在曲线下面,是凸函数。
拐点是两边凹凸不一致的点。数学上来讲,就是该点二阶导数为0,左边右边二阶导数都不为0并且正负号不同。
积分是什么?
38. 积分就是以直代曲的另一个应用。不过微分我们近似的是函数值,用导数(切线的斜率)和自变量的增量乘积来近似。积分近似的是函数曲线下的面积,用函数值和自变量的增量乘积的和来近似。
定义就是,把某段区间划分为n份,![]() 为最大的划分间隔。如果
为最大的划分间隔。如果![]() 这个极限存在,那么函数曲线与横轴构成的面积可以用该极限来近似。
这个极限存在,那么函数曲线与横轴构成的面积可以用该极限来近似。 。这里的间隔划分可以随意,但为了方便或者怎样,一般都是等间隔划分。这里的关键是该极限存在。
。这里的间隔划分可以随意,但为了方便或者怎样,一般都是等间隔划分。这里的关键是该极限存在。
39. 积分的性质有哪些可以推出来?
因为积分是乘积和的极限,如38所示。很容易可以推出齐次性,可加性,面积有正负,面积的大小和函数有关,积分可以分解为在两个区间上的积分。
由极限又可以推出,积分面积大于最小面积![]() ,小于最大面积
,小于最大面积![]() ,那么一定存在一个
,那么一定存在一个![]() .
.![]()
40. 积分函数是什么,积分函数的导数是什么?
积分函数是积分区间上限是一个自变量。
那么根据导数定义可以证明,积分函数的导数是用来积分的函数,称为导函数,积分函数称为原函数。
牛顿-莱布尼兹公式讲的就是积分可以用原函数来计算。
41. 原函数与积分上限函数的关系是什么?什么是不定积分?不定积分和原函数的关系是什么?
当函数连续时,原函数就是积分上限函数。不连续时,这两个之间不能划等号。
42. 积分的一些技术以及其证明
43. 判断反常积分是不是收敛?
反常积分是积分区间包含无穷的函数的积分。要么自变量趋向无穷,要么函数值趋向无穷。
因此证的关键是![]() 存不存在。f(x)>0。
存不存在。f(x)>0。
证明极限是否存在,第一种是看其是否单调有界。第二种看她如果大于一个函数,那个函数是发散的,那么这个F(x)也是发散的。如果小于某个函数且收敛,那么该函数极限也是存在的。
第三种是f(x)与![]() 比较。
比较。![]() ,该函数积分收敛。
,该函数积分收敛。![]() ,该函数积分发散。这里用
,该函数积分发散。这里用![]()
44. 微分方程是什么?微分方程的通解和特解是个啥?
微分方程是含有导函数和未知变量的方程,想要求解到的是该导函数的原函数。导数的原函数是一系列的函数![]() ,可以看成一个线素场。这一系列的原函数称为该方程的通解。如果原函数经过特定点,那么可以得到特解
,可以看成一个线素场。这一系列的原函数称为该方程的通解。如果原函数经过特定点,那么可以得到特解![]() 。此外,通解也不一定代表该微分方程的所有解。
。此外,通解也不一定代表该微分方程的所有解。
45. 什么是线性方程?
变量次方数为一次的是线性。分为齐次方程和非齐次方程。这样来看,矩阵也是线性方程。D算子可以用矩阵来表示。列向量分别表示x的不同阶数。那么三阶的D算子应为![]()
![]() 称为微分算子,是矩阵,也是线性函数。
称为微分算子,是矩阵,也是线性函数。
46. 微分方程的解得结构是什么?
由于可以把D当做矩阵,那么就是求线性方程组的解。如果是齐次微分方程,通解可以直接的出;如果是非齐次微分方程,解由通解和特解构成。
46. 怎么求解常系数微分方程?
![]() 的特征向量是
的特征向量是![]() (如果把
(如果把![]() 当做举阵的话),特征值为
当做举阵的话),特征值为![]() . 因为
. 因为![]()
即求通解。找出r的值,找到特征向量。通解即是特征向量的线性组合。
怎么求非齐次变系数微分方程?
先求出齐次方程的通解。再令解为u(x)*通解(常数变易),代入方程,求出u(x)。
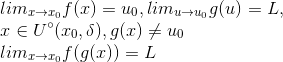
![\\b_{n}\prod_{n}^{i=0}(x-x_i) \\ b_{n}=\frac{f[x_{0},...,x_{n}]-f[x_{0},...,x_{n-1}]}{x_{n}-x_{0}}](http://img.e-com-net.com/image/info8/2e78b024f8fe418b98fd783ccd8e2958.gif)