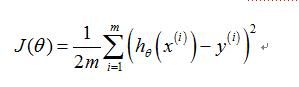coursera机器学习课程——Programming Exercise 1:Linear Regression
Programming Exercise 1:Linear Regression
本文主要是对coursera上机器学习课程第一次编程作业中英文pdf的个人翻译及涉及的程序的编写,编译环境为matlab。
本训练会使用线性回归,并观察他怎么应用在数据上。
Files included in this exercise
ex1.m,ex1_multi.m,ex1data1.txt,ex1data2.txt,submit.m
需要去填写完成的程序
warmUpExercise.m,plotData.m,computeCost.m,gradientDescent.m,computeCostMulti.m,gradientDescentMulti.m,featureNormalize.m,normalEqn.m
本次练习中会用到ex1.m和ex1_multi.m。这俩脚本程序会配置问题所需要数据和调用你需要写的代码。不需要改动他们。只需要完成第一部分,第二部分是选作的。有兴趣也可以写第二部分,我写了。
1.Simple Octave/Matlab function
ex1.m的第一部分帮你训练octave/matlab,在warmUpExercise.m中,你会发现一个Octave/MATLAB函数的框架。通过填入以下代码来修改它,返回一个5*5的单位矩阵。
A=eye(5);
完成后会生成一个对角单位阵,现在ex1.m会暂停,直到你按下任意键。他会接下来完成任务的其他部分。如果你想退出,按下ctrl-c。
1.1submitting Solutions
完成训练中的一部分后,可以使用submit函数上传你的答案,来获得评分。
2.单变量线性回归
本部分,你会使用单变量线性回归来预测食物货车的收益。假设你是一个餐馆的CEO,并想在不同的城市来开分店。城市链之间有货车来送,并且你有了不同城市的收益和人口的数据。你想用这些数据来帮你选择哪个城市来开下一家店。
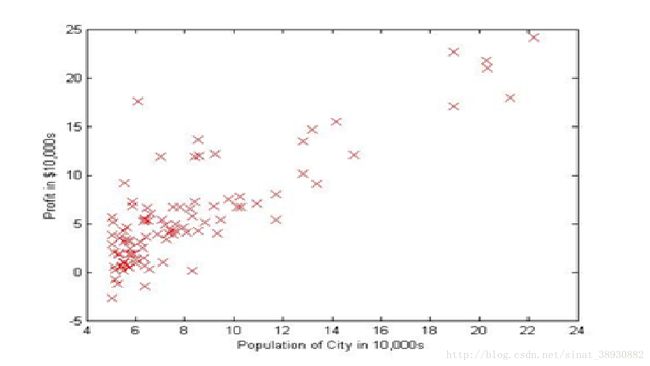
文件ex1data1.txt包含了用于我们线性回归问题的数据集。第一列是城市人口,第二列是该城食物货车的收益。负值说明了收益减少。ex1.m已经为你准备好了这些数据。2.1plotting the data
在开始任何工作之前,首先把数据可视化是很有用的。对于这个数据集,能够使用离散画图来可视化这些数据,由于它只含有两种属性来画图(profit&population)。其他很多你在实际生活中遇到的情况可能是多维的,而不能通过2D来画出来。
Ex1.m中,数据集从数据文件中load出来,成为变量x和y。
data = load('ex1data1.txt');
X = data(:, 1); y = data(:, 2);
m = length(y); % number of training examples
接下来,脚本会调用plotData函数来画出数据。任务是完成plotData.m,修改文件,并填入以下代码。
plot(x, y, ' rx' , ' MarkerSize' , 10); % Plot the data
ylabel(' Profit in $10,000s' ); % Set the y−axis label
xlabel(' Population of City in 10,000s' ); % Set the x−axis label
现在,当你继续运行ex1.m时,我们的结果可能如图1.
function plotData(x, y)
%PLOTDATA Plots the data points x and y into a new figure
% PLOTDATA(x,y) plots the data points and gives the figure axes labels of
% population and profit.
figure; % open a new figure window
% ====================== YOUR CODE HERE ======================
% Instructions: Plot the training data into a figure using the
% "figure" and "plot" commands. Set the axes labels using
% the "xlabel" and "ylabel" commands. Assume the
% population and revenue data have been passed in
% as the x and y arguments of this function.
%
% Hint: You can use the 'rx' option with plot to have the markers
% appear as red crosses. Furthermore, you can make the
% markers larger by using plot(..., 'rx', 'MarkerSize', 10);
plot(x,y,'rx','MarkerSize',10);
ylabel('Profit in $10,000s');
xlabel('Population of City in 10,000s');
% ============================================================
end
2.2GradientDescent
这一部分,使用梯度下降法来适应线性回归参数θ。
2.2.1UpdateEquations
线性回归的目的是最小化costfunction
其中假设函数通过以下线性模型给出
回想,你的模型的参数是theta_j值。这是你需要修改的值来最小化cost函数J(theta)。一个方法是使用批量梯度下降算法。在批量梯度下降算法中,每次迭代更新
随着梯度下降的每一步,你的参数会逐渐接近最优值,会获得最低的花费J(theta)。
Implementation Note:我们以列的形式在矩阵X中存储每一个样本。为了计算截断项(theta_0),我们给X添加了额外第一列,并全设为1.这允许我们把theta_0当做一个单独的其他特征。
2.2.2Implementation
在ex1.m中,我们已经配置好线性回归的数据。在接下来的几行,我们为我们的数据添加其他维来适应截断项theta_0。我们初始化参数为0并且学习步长alpha=0.01。
X = [ones(m, 1), data(:,1)]; % Add a column of ones to x
theta = zeros(2, 1); % initialize fitting parameters
% Some gradient descent settings
iterations = 1500;
alpha = 0.01;
2.2.3Computing the cost
当运行梯度下降来最小化costfunction时,计算cost来控制收敛是很有用的。在这一部分,你会利用一个函数来计算J(theta)以使你能够检查你的梯度下降的收敛性。
你的下一个任务是完成文件computeCost.m中的代码,这是一个计算J(theta)的函数。当写代码时记住,X和y不是标量值,但矩阵的行向量表示训练集中的样本。
一旦你完成了这个函数,ex1.m的下一步会运行computeCost,θ初始化为0,你会看到运行后的结果。Cost=32.07
function J = computeCost(X, y, theta)
%COMPUTECOST Compute cost for linear regression
% J = COMPUTECOST(X, y, theta) computes the cost of using theta as the
% parameter for linear regression to fit the data points in X and y
% Initialize some useful values
m = length(y); % number of training examples
% You need to return the following variables correctly
J = 0;
% ====================== YOUR CODE HERE ======================
% Instructions: Compute the cost of a particular choice of theta
% You should set J to the cost.
for i=1:m
J=J+(sum((X(i,:)*theta-y(i))^2)/(2*m));
end
% =========================================================================
end
2.2.4Gradientdescent
下一步,你会在gradientDescent.m中应用梯度下降。已经给你写好了循环结构,你只需要在每次迭代中更新θ。
在程序中,确保你明白你想要最优化什么,和什么被更新了。记住cost被向量θ参数化,而不是X和y。因此我们通过改变θ的值来最小化J(theta),而不是改变X或y。
一个证明梯度下降好用的方法是看J(theta)的值,并检测他在每次迭代中确实在下降。gradientDescent.m开始的代码在每次迭代中调用了computeCost,并打印出cost。假设你已经正确地使用了梯度下降和computeCost,你的J(theta)应该不会增加,并会在算法的最后收敛到一个确定的值。
当你完成后,ex1.m会使用你最后的参数画出相应曲线。结果如图2.
你最后的θ值将会被用来预测35000和70000人数的收益。注意到下面几行在ex1.m中使用矩阵乘法,而不是求和或循环。
predict1 = [1, 3.5] * theta;
predict2 = [1, 7] * theta;
function [theta, J_history] = gradientDescent(X, y, theta, alpha, num_iters)
%GRADIENTDESCENT Performs gradient descent to learn theta
% theta = GRADIENTDESCENT(X, y, theta, alpha, num_iters) updates theta by
% taking num_iters gradient steps with learning rate alpha
% Initialize some useful values
m = length(y); % number of training examples
J_history = zeros(num_iters, 1);
for iter = 1:num_iters
% ====================== YOUR CODE HERE ======================
% Instructions: Perform a single gradient step on the parameter vector
% theta.
%
% Hint: While debugging, it can be useful to print out the values
% of the cost function (computeCost) and gradient here.
%
theta(1) = theta(1) - alpha/m*sum((X*theta-y).*X(:,1));
theta(2) = theta(2) - alpha/m*sum((X*theta-y).*X(:,2));
% ============================================================
% Save the cost J in every iteration
J_history(iter) = computeCost(X, y, theta);
end
end
2.3Debugging
使用梯度下降时有几处需要注意:
A.Octave/matlab中序列序号开始自1而不是0,。如果存储为theta中的向量theta_0和theta_1,必须为theta(1)和theta(2)。
B. 如果程序运行时有很多错误,检查矩阵来确保你在加或乘中矩阵维度一致。用size命令看变量的维度可能会帮助你。
C.Octave/Matlab中数学运算通常为矩阵运算,这可能是尺寸不匹配错误的来源之一,如果不想要矩阵乘,要加点,点乘和乘是不一样的。
2.4可视化J(theta)
为了更好地了解cost函数J(theta),你应该把这个cost通过theta_0和theta_1来二维画出来。你不用为这一部分写新的code,但你需要知道你已经写的代码怎样画出这幅图。
在ex1.m的下一步中,调用了你在computeCost中写的代码来计算J(theta)。
% initialize J vals to a matrix of 0' s
J vals = zeros(length(theta0 vals), length(theta1 vals));
% Fill out J vals
for i = 1:length(theta0 vals)
for j = 1:length(theta1 vals)
t = [theta0 vals(i); theta1 vals(j)];
J vals(i,j) = computeCost(x, y, t);
end
end
当这几行处理过后,你会得到2维的的值。Ex1.m会接着使用surf和contour命令通过这些值来产生的表面和轮廓线。画的图像如图3.
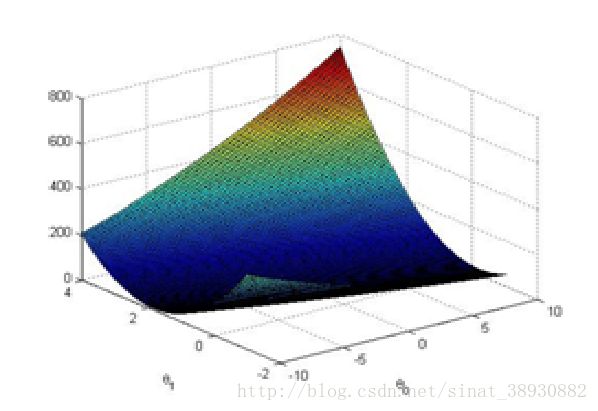
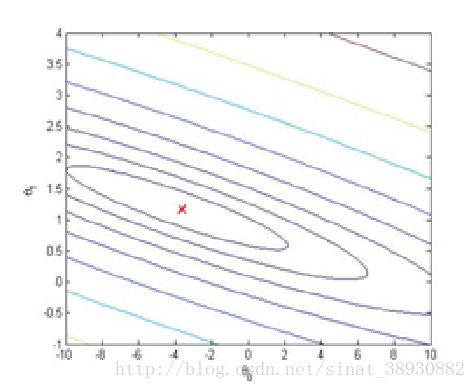
这些图的目的是给你展示J(theta)怎么随着theta_0和theta_1而改变。Cost函数J(theta)是碗型的,并有全局最小值。这个最小值就是对于heta_0和theta_1的最优值,每次迭代都接近这个点。
%% Machine Learning Online Class - Exercise 1: Linear Regression
% Instructions
% ------------
%
% This file contains code that helps you get started on the
% linear exercise. You will need to complete the following functions
% in this exericse:
%
% warmUpExercise.m
% plotData.m
% gradientDescent.m
% computeCost.m
% gradientDescentMulti.m
% computeCostMulti.m
% featureNormalize.m
% normalEqn.m
%
% For this exercise, you will not need to change any code in this file,
% or any other files other than those mentioned above.
%
% x refers to the population size in 10,000s
% y refers to the profit in $10,000s
%
%% Initialization
clear ; close all; clc
%% ==================== Part 1: Basic Function ====================
% Complete warmUpExercise.m
fprintf('Running warmUpExercise ... \n');
fprintf('5x5 Identity Matrix: \n');
warmUpExercise()
fprintf('Program paused. Press enter to continue.\n');
pause;
%% ======================= Part 2: Plotting =======================
fprintf('Plotting Data ...\n')
data = load('ex1data1.txt');
X = data(:, 1); y = data(:, 2);
m = length(y); % number of training examples
% Plot Data
% Note: You have to complete the code in plotData.m
plotData(X, y);
fprintf('Program paused. Press enter to continue.\n');
pause;
%% =================== Part 3: Cost and Gradient descent ===================
X = [ones(m, 1), data(:,1)]; % Add a column of ones to x
theta = zeros(2, 1); % initialize fitting parameters
% Some gradient descent settings
iterations = 1500;
alpha = 0.01;
fprintf('\nTesting the cost function ...\n')
% compute and display initial cost
J = computeCost(X, y, theta);
fprintf('With theta = [0 ; 0]\nCost computed = %f\n', J);
fprintf('Expected cost value (approx) 32.07\n');
% further testing of the cost function
J = computeCost(X, y, [-1 ; 2]);
fprintf('\nWith theta = [-1 ; 2]\nCost computed = %f\n', J);
fprintf('Expected cost value (approx) 54.24\n');
fprintf('Program paused. Press enter to continue.\n');
pause;
fprintf('\nRunning Gradient Descent ...\n')
% run gradient descent
theta = gradientDescent(X, y, theta, alpha, iterations);
% print theta to screen
fprintf('Theta found by gradient descent:\n');
fprintf('%f\n', theta);
fprintf('Expected theta values (approx)\n');
fprintf(' -3.6303\n 1.1664\n\n');
% Plot the linear fit
hold on; % keep previous plot visible
plot(X(:,2), X*theta, '-')
legend('Training data', 'Linear regression')
hold off % don't overlay any more plots on this figure
% Predict values for population sizes of 35,000 and 70,000
predict1 = [1, 3.5] *theta;
fprintf('For population = 35,000, we predict a profit of %f\n',...
predict1*10000);
predict2 = [1, 7] * theta;
fprintf('For population = 70,000, we predict a profit of %f\n',...
predict2*10000);
fprintf('Program paused. Press enter to continue.\n');
pause;
%% ============= Part 4: Visualizing J(theta_0, theta_1) =============
fprintf('Visualizing J(theta_0, theta_1) ...\n')
% Grid over which we will calculate J
theta0_vals = linspace(-10, 10, 100);
theta1_vals = linspace(-1, 4, 100);
% initialize J_vals to a matrix of 0's
J_vals = zeros(length(theta0_vals), length(theta1_vals));
% Fill out J_vals
for i = 1:length(theta0_vals)
for j = 1:length(theta1_vals)
t = [theta0_vals(i); theta1_vals(j)];
J_vals(i,j) = computeCost(X, y, t);
end
end
% Because of the way meshgrids work in the surf command, we need to
% transpose J_vals before calling surf, or else the axes will be flipped
J_vals = J_vals';
% Surface plot
figure;
surf(theta0_vals, theta1_vals, J_vals)
xlabel('\theta_0'); ylabel('\theta_1');
% Contour plot
figure;
% Plot J_vals as 15 contours spaced logarithmically between 0.01 and 100
contour(theta0_vals, theta1_vals, J_vals, logspace(-2, 3, 20))
xlabel('\theta_0'); ylabel('\theta_1');
hold on;
plot(theta(1), theta(2), 'rx', 'MarkerSize', 10, 'LineWidth', 2);