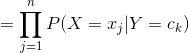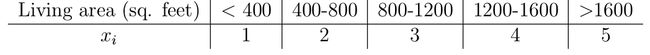朴素贝叶斯（详细版）
朴素贝叶斯是传统机器学习算法中的一种，因为使用简单而且效果不差而被广泛使用。基本上用到的数学原理就是贝叶斯公式和极大似然估计，原理上也是比较简单。但是它的简单是源于做了一个硬性的假设，假设在知道y的情况下，x中的所有feature出现的可能性是相互独立的，这个条件其实并不成立，但是这个假设大大简化了模型，不过这个模型也因为这个硬性假设而丧失了一些准确性。
这篇博文的内容是基于《统计学习方法》中第四章和cs229中第5课的学习和理解。这里的符号表示还是根据自己的习惯来，用上标表示样本数，用下标表示feature数，比如
表示第i个样本中的第j个feature。
朴素贝叶斯
符号表示
现在假设我们有m组训练样本
，我们需要根据这m组样本学习到x与y之间的隐藏联系，从而当给定一个x的数据时，能够预测出y的值。
假设y的取值范围有K类，分别是
同时假设每个
的feature有n个，分别是
，而每个feature的也就是
第j个feature的取值一种有
种，表示为
为了更好的理解符号表示，可以举一个例子，邮件自动分类问题。
比如我们希望邮箱可以自动将邮件分类为工作邮件(0)，私人邮件(1)，垃圾邮件(2)这样三类，分别用0,1,2表示，那么y的取值范围有
，并且
x就是我们的邮件内容，使用单词表对邮件内容进行编码。编码方式是如果邮件中的某个字符出现在了单词表中，那么这个位置的值就为1，否则为0.
假如我们的单词表有50000个单词，而我们的邮件内容为...buy a toy, price...，那么我们根据单词表的编码为
，
所以x的feature n=50000，每个feature的取值有2中
，
希望这个例子能够对理解符号有帮助。
生成模型
为了求出给定x的情况下y的取值概率，我们使用生成模型的方式来计算，因此可以使用贝叶斯公式
关于这个式子我们的目的就是找到一个
使得
概率最大，可以表示为
等同于
因为当给定了x后无论取何值，
都是一样的，所以这个式子又等同于
现在分解这个式子里面的每个概率问题，首先是
，因为x这个需要用来预测的样本不一定会出现在训练集中，所以我们不能用极大似然估计来计算他的概率，那么可以转换为条件概率来计算。
这是很难计算的，所以就引出了朴素贝叶斯的假设。
假设：
就是说在知道y的结果的情况下，x中每个feature出现的概率相互独立，其实这个假设是不真实的，比如上面的邮件例子，如果这封邮件是垃圾邮件，x中出现了buy等词，那么很可能会出现price。
虽然说这个假设不准确，但是在实际使用的效果不算太差，所以应用还是比较广泛。
那么我们的问题就变成了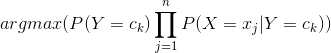
（1），要找到一个类别使这个式子最大，那么这个就是我们预测的类别。
那如何来求
和
呢，就是根据我们的训练样本来对他们进行极大似然估计。
其实就表示所有训练样本中y为出现的次数除以总的训练样本数
，
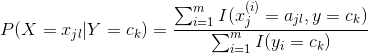表示x第j个feature的所有取值中，取值为第l个值的情况。注意这里的表示方法和《统计学习方法》中有点差别，因为我们是用上表表示第几样本，用下标表示第几个feature。所以这个含义就是所有样本中x的第j个feature取第i个值，并且y取的值的个数除以样本中y的值为的个数。
通过这种分步求解的方法就可以计算中让式子1最大的，从而做出预测。
应用练习
《统计学习方法》中有一个很简单的例子，可以很好的展示如何进行操作。
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
 |
1 | 1 | 1 | 1 | 1 | 2 | 2 | 2 | 2 | 2 | 3 | 3 | 3 | 3 | 3 |
 |
S | M | M | S | S | S | M | M | L | L | L | M | M | L | L |
 |
-1 | -1 | 1 | 1 | -1 | -1 | -1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | -1 |
看上面这个表格是15组训练样本，
是
的两个特征（feature），的取值集合为
，的取值集合为
，的取值集合为
现在有一个
的例子，要预测它的y值是1还是-1.
解答：
先求
而
，
，
，
所以
再求
所以对于的情况，我们预测y=-1
拉普拉斯平滑
考虑到存在概率为0的情况，如果y取在训练样本中没有出现，那么我们求会出错，为了防止这种情况增加一种平滑处理的方式。
，其中为x的第j个feature的所有可能的个数。
如果
就是Laplace smoothing，拉普拉斯平滑。
同样
，其中K为Y的所有可能取值数，如果就是Laplace smoothing。
增加了拉普拉斯平滑后对上面那个计算的例子再来计算一次看看结果
同样预测结果应该是-1
应用扩展
1.朴素贝叶斯适合离散型数据的处理，但是对于一些连续性数据也可以考虑转换成离散形式进行预测。比如连续的房价问题可以根据区间转换为离散问题来分析。
2.关于上面提到过的邮件分类的问题，也可以换一个思路来建模。可以考虑n为邮件的长度，每个
的取值范围为
{1,2，...，#词库的长度}，所以=#词库的长度，这种方式建模可以考虑到邮件中单词重复出现的情况。