特征选择之遗传算法
遗传算法的优点:
1. 与问题领域无关切快速随机的搜索能力。
2. 搜索从群体出发,具有潜在的并行性,可以进行多个个体的同时比较,robust.
3. 搜索使用评价函数启发,过程简单
4. 使用概率机制进行迭代,具有随机性。
5. 具有可扩展性,容易与其他算法结合。
6. 遗传算法具有良好的全局搜索能力,可以快速地将解空间中的全体解搜索出,而不会陷入局部最优解的快速下降陷阱;是全局优化算法,一般的迭代方法容易陷入局部极小的陷阱而出现"死循环"现象,使迭代无法进行。遗传算法很好地克服了这个缺点,是一种全局优化算法。
遗传算法的缺点:
1、遗传算法的编程实现比较复杂,首先需要对问题进行编码,找到最优解之后还需要对问题进行解码,
2、另外三个算子的实现也有许多参数,如交叉率和变异率,并且这些参数的选择严重影响解的品质,而目前这些参数的选择大部分是依靠经验.
3、没有能够及时利用网络的反馈信息,故算法的搜索速度比较慢,要得要较精确的解需要较多的训练时间。
4、算法对初始种群的选择有一定的依赖性,能够结合一些启发算法进行改进。
5、算法的并行机制的潜在能力没有得到充分的利用,这也是当前遗传算法的一个研究热点方向。
在现在的工作中,遗传算法(1972年提出)已经不能很好的解决大规模计算量问题,它很容易陷入“早熟”。常用混合遗传算法,合作型协同进化算法等来替代,这些算法都是GA的衍生算法。
并且利用它的内在并行性,可以方便地进行分布式计算,加快求解速度。但是遗传算法的局部搜索能力较差,导致单纯的遗传算法比较费时,在进化后期搜索效率较低。在实际应用中,遗传算法容易产生早熟收敛的问题。采用何种选择方法既要使优良个体得以保留,又要维持群体的多样性,一直是遗传算法中较难解决的问题。
模拟退火算法虽具有摆脱局部最优解的能力,能够以随机搜索技术从概率的意义上找出目标函数的全局最小点。但是,由于模拟退火算法对整个搜索空间的状况了解不多,不便于使搜索过程进入最有希望的搜索区域,使得模拟退火算法的运算效率不高。模拟退火算法对参数(如初始温度)的依赖性较强,且进化速度慢。
http://blog.sina.com.cn/s/blog_6377a3100100h1mj.html
基于遗传算法的特征选择是一种wrapper方法,该算法是以支持向量机分类器的识别率作为特征选择的可分性判断依据。在遗传算法中,对所选择的特征用[0,1]二进制串来初始化,由于二进制数{0,1}是等概率出现的,所以最优特征个数的期望是原始特征个数的一半。要进一步减少特征个数,则可以让二进制数{0,1}以不等概率出现,以a个特征中选择b个特征为例,使得在a位二进制串中1出现的概率为b/ab/a。
对于支持向量机和遗传算法,可以看先前的博客《线性支持向量机》和《遗传算法及其实现》。
改进的遗传算法
一个完整的遗传算法主要包括几个步骤:基因编码,种群初始化,选择操作,交叉操作,变异操作,结束条件判断等。
基因编码
将选择的特征组合用一个{0,1}二进制串表示,0表示不选择对应的特征,1表示选择对应的特征。对惩罚参数C和核参数σσ也采用二进制编码,根据范围和精度计算所需要的二进制串长度分别为lc,lσlc,lσ。
种群初始化
以a个特征中选取b个特征为例,确保在前a位二进制串中1出现的概率一定是b/ab/a,两个参数部分的二进制码随机生成,二进制长度为la+lc+lσla+lc+lσ;然后以一定的种群规模进行种群初始化。
选择操作
计算个体适应度,即先对个体进行解码,再用训练和测试样本计算SVM的正确分类率:
fitness=WA×SVMacuracy+WF×(Σlai=1Ci×Fi)−1WA:SVM分类准确率权重,一般设置为75−100%SVMaccuracy:SVM分类准确率WF:选择特征和惩罚参数乘积和逆的权重,如果准确率非常重要,可以把它设置成100%Ci:特征i的损失,如果没有关于损失的信息,可以设置为1Fi:1代表选择了特征i;0表示没有选择特征i。fitness=WA×SVMacuracy+WF×(Σi=1laCi×Fi)−1WA:SVM分类准确率权重,一般设置为75−100%SVMaccuracy:SVM分类准确率WF:选择特征和惩罚参数乘积和逆的权重,如果准确率非常重要,可以把它设置成100%Ci:特征i的损失,如果没有关于损失的信息,可以设置为1Fi:1代表选择了特征i;0表示没有选择特征i。
然后采用轮盘赌选择法,随机从种群中挑选一定的数目个体,再将适应度最好的个体作为父体,这个过程重复进行直到完成所有个体的选择。
交叉操作
由于交叉操作的随机性,会改变前a位二进制串中的1出现的概率,使其不等于b/ab/a,这将导致不同个体特征矢量的维数不尽相同,所以进行以下操作。
首先将二进制编码分成两部分,前lala位特征编码部分和后lc+lσlc+lσ位参数编码部分。如下图所示, 
首先对比两个父体,找出两父体个体同为1的基因位,称之为“优势基因位”,例如第1,4位。然后找两父体其中一个为1的基因位,称之为“非优势基因位”,例如2,5,6,a。如果两父体中存在“优势基因位”,表明两父体对该基因位所对应的特征分量的选择意见趋于一致,该特征应在子代中予以保留。如果父代个体中存在“非优势基因位”,表明两个体在该特征上存在分歧。
如果两父体个体存在e个“优势基因位”,则在子代中保留这些基因位,在“非优势基因位”中随机选择b-e个基因位,并令这些基因位为1,产生两个新个体。图1中两个子个体保留了第1,4位,子个体1在第2,5,6,a中随机选择了第6,a位并令其成为1,子个体2第2,5,6,a位中随机选择了第2,5位并令其为1.这样保证了子个体与父体选择的特征数式中为b。
变异操作
如果对特征编码进行翻转变异操作,那么将使二进制串中的为1的基因位发生变化,如果某一位由0变成1,则选择的特征数变为d+1,反之变为d-1.为解决这个问题可以使用下面的方法。
如图2,分别统计编码为1和0的基因位,分别在为1和0的基因位中随机选择一个二进制数,图2是第2和第5位相互交换,得到变异子个体。 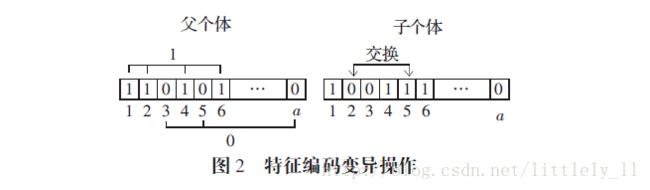
结束条件
前面的选择,交叉,变异操作合起来称为遗传操作,当遗传操作到达设定的最大迭代次数时,算法结束。如果迭代遗传过程中,连续若干代最优个体不再变化,算法也可提前结束。
下面是算法的流程图: 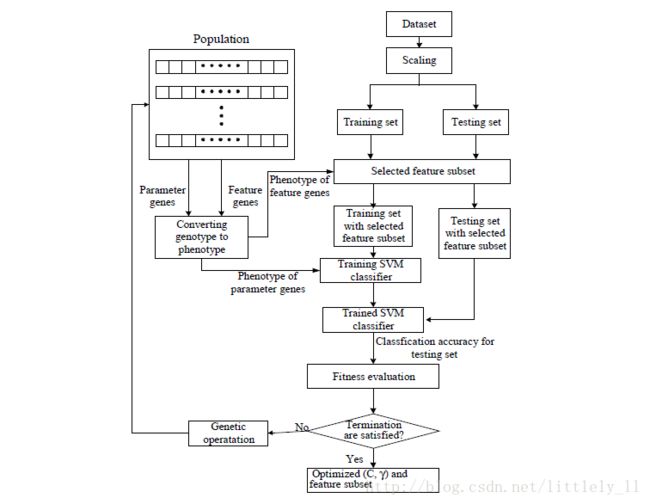
参考
【Cheng-Lung Huang , Chieh-Jen Wang】A GA-based feature selection and parameters optimization for support vector machines
【杜卓明,冯静】改进遗传算法和支持向量机的特征选择算法
原文链接。 https://blog.csdn.net/littlely_ll/article/details/72625312
智能优化算法和传统优化算法的区别:
-
优化算法有很多,关键是针对不同的优化问题,例如可行解变量的取值(连续还是离散)、目标函数和约束条件的复杂程度(线性还是非线性)等,应用不同的算法。
-
对于连续和线性等较简单的问题,可以选择一些经典算法,如梯度、Hessian 矩阵、拉格朗日乘数、单纯形法、梯度下降法等。
-
而对于更复杂的问题,则可考虑用一些智能优化算法,如遗传算法和蚁群算法,此外还包括模拟退火、禁忌搜索、粒子群算法等。
优缺点比较:
传统优化算法与遗传算法之间的优缺点和特点比较
原文 https://blog.csdn.net/misayaaaaa/article/details/54407490
传统优化算法与遗传算法之间的优缺点比较
传统优化算法优点:1:利用了解空间的特性,如可微等。
2:理论较为完善,计算量小。
3:收敛速度快。
4:具有确定的终止准则。
传统优化算法缺点:1:仅能求出优化问题的局部最优解。
2:求解的结果强烈依赖于初始值。
遗传算法的优点:1:能够求出优化问题的全局最优解。
2:优化结果与初始条件无关。
3:算法独立于求解域。
4:具有较强的鲁棒性。
5:适合于求解复杂的优化问题。
6:应用较为广泛。
遗传算法的缺点:1:收敛速度慢。
2:局部搜索能力差。
3:控制变量较多。
4:无确定的终止准则。
特点的比较:
遗传算法:1:以编码的方式工作,可以并行搜索多个峰值
2:以编码方式工作,不对参数本身进行操作,具有良好的可操作性
3:用概率性传递规则代替确定性规则,具有全局寻优特点
4:只使用目标函数和相应的适应度函数,不需要其他的辅助信息
传统优化算法:1:需要不同形式的辅助信息,如可微、连续等
2:有固定的结构和参数,计算复杂度和收敛性可做理论分析
3:有明确的条件描述,清晰的结构信息
智能优化算法总结
优化算法有很多,
经典算法包括:有线性规划,动态规划等;改进型局部搜索算法包括爬山法,最速下降法等,模拟退火、遗传算法以及禁忌搜索称作指导性搜索法。而神经网络,混沌搜索则属于系统动态演化方法。
梯度为基础的传统优化算法具有较高的计算效率、较强的可靠性、比较成熟等优点,是一类最重要的、应用最广泛的优化算法。但是,传统的最优化方法在应用于复杂、困难的优化问题时有较大的局限性。
一个优化问题称为是复杂的,通常是指具有下列特征之一:(1)目标函数没有明确解析表达;(2)目标函数虽有明确表达,但不可能恰好估值;(3)目标函数为多峰函数;(4)目标函数有多个,即多目标优化。
一个优化问题称为是困难的,通常是指:目标函数或约束条件不连续、不可微、高度非线性,或者问题本身是困难的组合问题。传统优化方法往往要求目标函数是凸的、连续可微的,可行域是凸集等条件,而且处理非确定性信息的能力较差。
这些弱点使传统优化方法在解决许多实际问题时受到了限制。
智能优化算法一般都是建立在生物智能或物理现象基础上的随机搜索算法,目前在理论上还远不如传统优化算法完善,往往也不能确保解的最优性,因而常常被视为只是一些“元启发式方法”(meta-heuristic)。但从实际应用的观点看,这类新算法一般不要求目标函数和约束的连续性与凸性,甚至有时连有没有解析表达式都不要求,对计算中数据的不确定性也有很强的适应能力。
下面给出一个局部搜索,模拟退火,遗传算法,禁忌搜索的形象比喻:
为了找出地球上最高的山,一群有志气的兔子们开始想办法。
1.兔子朝着比现在高的地方跳去。他们找到了不远处的最高山峰。但是这座山不一定是珠穆朗玛峰。这就是局部搜索,它不能保证局部最优值就是全局最优值。
2.兔子喝醉了。他随机地跳了很长时间。这期间,它可能走向高处,也可能踏入平地。但是,他渐渐清醒了并朝最高方向跳去。这就是模拟退火。
3.兔子们吃了失忆药片,并被发射到太空,然后随机落到了地球上的某些地方。他们不知道自己的使命是什么。但是,如果你过几年就杀死一部分海拔低的兔子,多产的兔子们自己就会找到珠穆朗玛峰。这就是遗传算法。
4.兔子们知道一个兔的力量是渺小的。他们互相转告着,哪里的山已经找过,并且找过的每一座山他们都留下一只兔子做记号。他们制定了下一步去哪里寻找的策略。这就是禁忌搜索。
一般而言,局部搜索就是基于贪婪思想利用邻域函数进行搜索,若找到一个比现有值更优的解就弃前者而取后者。但是,它一般只可以得到“局部极小解”,就是说,可能这只兔子登“登泰山而小天下”,但是却没有找到珠穆朗玛峰。而模拟退火,遗传算法,禁忌搜索,神经网络等从不同的角度和策略实现了改进,取得较好的“全局最小解”。
https://blog.csdn.net/sinde1992/article/details/50321225