数据标准化 Data Normalization
在一些实际问题中,我们得到的样本数据都是多个维度的,即一个样本是用多个特征来表征的。比如在预测房价的问题中,影响房价y的因素有房子面积x1、卧室数量x2等。这里的x1,x2又被称为特征。很显然,这些特征的量纲和数值得量级都是不一样的,在预测房价时,如果直接使用原始的数据值,那么他们对房价的影响程度将是不一样的,而通过标准化处理,可以使得不同的特征具有相同的尺度(Scale)。
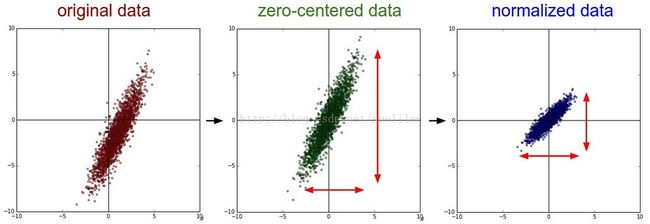
下图最左是原始数据;中间是中心化数据,就是平移到原点;最右是z-score规范后的数据,均值为0,方差为1。
一、数据标准化的意义:
1、数据的量纲不同;数量级差别很大
经过标准化处理后,原始数据转化为无量纲化指标测评值,各指标值处于同一数量级别,可进行综合测评分析。
如果直接用原始指标值进行分析,就会突出数值较高的指标在综合分析中的作用,相对削弱数值水平较低指标的作用。
2、避免数值问题:太大的数会引发数值问题。
3、平衡各特征的贡献
一些分类器需要计算样本之间的距离(如欧氏距离),例如KNN。
如果一个特征值域范围非常大,那么距离计算就主要取决于这个特征,从而与实际情况相悖(比如这时实际情况是值域范围小的特征更重要)。
4、一些模型求解的需要:加快了梯度下降求最优解的速度
二、数据标准化的方法
1、Min-Max标准化
x = (x - min)/(max - min)
通过对数据的每一个维度的值进行重新调节,使得最终的数据向量落在 [0,1]区间内
应用场景:
这种归一化方法比较适用在数值比较集中的情况。但是,如果max和min不稳定,很容易使得归一化结果不稳定,使得后续使用效果也不稳定,实际使用中可以用经验常量值来替代max和min。而且当有新数据加入时,可能导致max和min的变化,需要重新定义。
在不涉及距离度量、协方差计算、数据不符合正太分布的时候,可以使用该方法。
在处理自然图像时,我们获得的像素值在 [0,255] 区间中,常用的处理是将这些像素值除以 255,使它们缩放到 [0,1]中.
2、标准差标准化,也叫z-score标准化
x =(x - u)/σ u是均值 σ是标准差
处理后的数据符合标准正态分布。该标准化方法广泛用于机器学习算法(SVM,Logistic regression,neural networks)
应用场景
在分类、聚类,算法中需要使用距离来度量相似性的时候、或者使用PCA(协方差分析)技术进行降维的时候,Z-score 标准化表现更好。
3、非线性归一化
经常用在数据分化比较大的场景,有些数值很大,有些很小。通过一些数学函数,将原始值进行映射。该方法包括 log、指数,正切等。需要根据数据分布的情况,决定非线性函数的曲线。
(1)log函数转化到[0,1]。数据要落到[0,1]区间,要求原数据大于等于1
(2)atan反正切函数。要想数据落到[0,1],数据应该大于等于0,小于0的数据被映射到[-1,0]
(3)logistic函数 | sigmoid函数:该函数的曲线是S型的,值域在[0,1]范围
三、处理哪些问题时需要对数据进行标准化?
1、分类(如k-nearest neighbors算法)
2、聚类(如k-means算法)
使用距离(如欧几里得距离)来判定样本之间的相似度的分类和聚类问题,都要进行数据规范化。
3、支持向量机SVM(support vector machine),逻辑回归logistic regression, perceptron, neural networks etc.
上面这些问题使用梯度优化来获得最优解。比如支持向量机使用梯度优化得到将样本数据分开的最优超平面。
ifyou are using 梯度下降优化算法(gradientdescent/ascent-based optimization), otherwise some weights will update muchfaster than others
4、主成分分析(principal component analysis), linear discriminant analysis, kernel principal component analysis
sinceyou want to find directions of maximizing the variance (under the constraintsthat those directions/eigenvectors/principal components are orthogonal); youwant to have features on the same scale since you’d emphasize variables on“larger measurement scales” more.
总之,涉及到距离、协方差(比如PCA本质涉及协方差计算)、梯度计算的问题要进行标准化。
距离、协方差,是因为要使各特征贡献一致所以使用标准化
梯度计算,是因为如果不标准化,模型的收敛会很慢或者不会收敛到最优解。