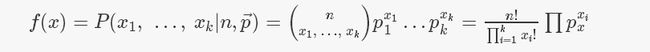几个简单数学分布

1. 概率密度函数

---

假如我们要预测明天的下雨量，x表示下雨的量，f(x)就表示为概率密度，我们随便画一个概率密度，他们的关系如下：

其中概率密度函数f(x)并不代表概率，只是代表当前x点的概率密度，类似于速度不代表位移一样，我们把所有可能发生事件概率相加应该为1(上图面积)：

∫+∞−∞f(x)dx=1

其中f(x)>=0，也可以计算下雨量在某个范围内的概率：

P(a<x<b)=∫abf(x)dx=1

积分后的概率即成为概率分布。

2. 二项分布

---

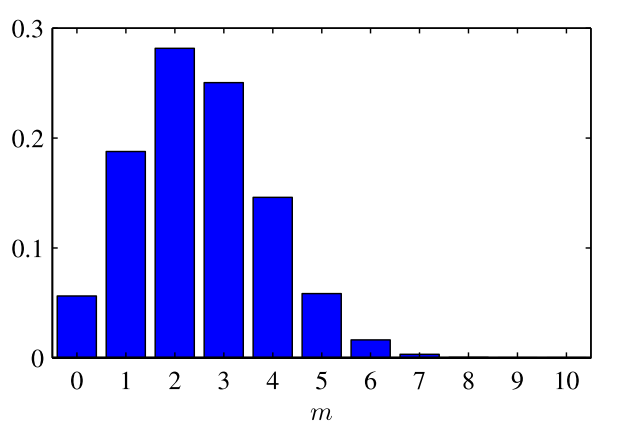
抛硬币是典型的二线分布，假设我们抛了5次硬币，设定P(x)表示有x次硬币正面朝上的话，我们可以得到一个类似如下的概率分布：

其中x为正面朝上的次数，离散变量和连续变量的差别可以看下面的泊松分布。

3. 泊松分布

---

泊松分布是二项分布的极限情况。

假设我们现在要估计某个路口一小时经过k辆车的概率，第一步我们需要先大量的观察一段时间，获得一个一小时内通过汽车数量的期望λ。

然后我们把一小时分为60分钟，同时假设每一分钟要么经过一辆车，要么没有车，那么按照二项分布的式子：

P(k)=Ck60(λ60)k(1−λ60)60−k

也就是说，期望除以60分钟（把一小时分成60份）获得每一分钟有一辆车经过的概率。

但是很明显我们不能确保每分钟真的只过一辆，为了更加精确，我们可以把一小时继续分为3600秒或72000个半秒，也就是说分的越多份，越精确。如果我们这么一直分下去，我们就获得了泊松分布，也就是二项分布的极限情况。

如果引入极限和e，泊松分布可以表达为(参考这里)：

P(X=k)=e−λλkk!

泊松分布的概率密度和累计概率图像如下： 

4. 正态分布

---

跟泊松分布一样，正态分布其实也是在大量观察现实世界的接触上总结推理出来的，它的概率密度函数为：

f(x)=12π−−√σe−(x−μ)22σ2

图像类似：

其中μ为观察到的数据的均值，是期望的一种估计方式，类似上面泊松分布估计用的期望,在图上表示为中心点的位置。

σ是样本的标准差，在图上可以表现为向中央的紧缩程度。

正态分布的特点是大自然中很多事件都符合它的描述，比如20岁男子的身高、同一个学校里学生的成绩分布等等。

正态分布还有一个有趣的特点是：

1. 横轴区间（μ-σ，μ+σ）内的面积(即概率)为68.268949%
   
2. 横轴区间（μ-1.96σ，μ+1.96σ）内的面积为95.449974%
   
3. 横轴区间（μ-2.58σ，μ+2.58σ）内的面积为99.730020%
   

正态分布可以通过调整其两个参数能够拟合很多自然界的情况，也可以和其他分布在某些情况下互相转换。

5. Gamma分布

---

正态分布的特点是左右对称，这个世界也有很多不符合这种分布的情况，比如某个事件的热度，可能会先迅速上升，然后缓慢降低热度，还有发射火箭的速度等等。

Gamma分布的概率密度函数为：

其中α为形状参数，表示分布的形状，β为尺度参数，表示左右两边的对称情况，数值越大越对称，无限大时区域正态分布。

下图中k=α,θ=β:

数据的期望可以表示为:E(X)=α/β, D(X)=β/(α2)

从物理意义上说，Gamma分布表示第α件事情发生时所需等待的时间. b表示某事件发生需要的时间

Gamma(a,b)表示第α件事情发生时所需等待的时间

让我们先通过一个例子，了解什么是"泊松分布"。

已知某家小杂货店，平均每周售出2个水果罐头。请问该店水果罐头的最佳库存量是多少？

假定不存在季节因素，可以近似认为，这个问题满足以下三个条件：

（1）顾客购买水果罐头是小概率事件。

（2）购买水果罐头的顾客是独立的，不会互相影响。

（3）顾客购买水果罐头的概率是稳定的。

在统计学上，只要某类事件满足上面三个条件，它就服从"泊松分布"。

泊松分布的公式如下：

各个参数的含义：

　　P：每周销售k个罐头的概率。

　　X：水果罐头的销售变量。

　　k：X的取值（0，1，2，3...）。

　　λ：每周水果罐头的平均销售量，是一个常数，本题为2。

根据公式，计算得到每周销量的分布：

从上表可见，如果存货4个罐头，95%的概率不会缺货（平均每19周发生一次）；如果存货5个罐头，98%的概率不会缺货（平均59周发生一次）。

http://www.ruanyifeng.com/blog/2013/01/poisson_distribution.html

http://sobuhu.com/math/2013/06/17/distributions.html

需要注意的是概率密度函数和概率的关系

密度这个概念的理解的确不那么简单
事实上，对于连续型随机变量，例如X服从正态分布，
那么X在每一点的概率都是0，但是X在一个区间内的概率却不是0
这不难理解，就像一根质量分布不均匀的钢笔，钢笔在每个点上的质量都是0，
但是钢笔在一个小块儿内的质量却不是0

对于这种随机变量X怎么研究呢？很简单！
设dx是一个非常小的正数，因为任何函数在一个很小的区间上都可以近似看成线性的，那
么X处于(x,x+dx)内的概率一定可以近似表示成f(x)dx的形式
这里的f(x)就叫做X的概率密度

不止是概率密度，物理上的各种密度的原理都是这样的

你可能会问，为什么X在每一点的概率都是0，但是X在一个区间内的概率却不是0？
这是因为概率论的公理体系只能保证可列个概率为0的事件的并还是概率为0的
然而一个区间包含不可列个点！因此尽管这些点的概率都是0，
它们的并，也就是这个区间的概率却可以不是0

对于离散型的概率密度函数，取一个x值，获得的就是取x时的概率

对于连续性的，必须是要取一个区间的，概率才有意义

3. 伯努利、二项分布、多项分布

伯努利分布就是对单次抛硬币的建模，X~Bernoulli(p)的PDF为f(x)=px(1−p)1−x，随机变量X只能取{0, 1}。对于所有的pdf，都要归一化！而这里对于伯努利分布，已经天然归一化了，因此归一化参数就是1。

很多次抛硬币的建模就是二项分布了。注意二项分布有两个参数，n和p，要考虑抛的次数。

二项分布的取值X一般是出现正面的次数，其PDF为：

Cxn就是二项分布pdf的归一化参数。如果是beta分布，把Cxn换成beta函数分之一即可，这样可以从整数情况推广为实数情况。所以beta分布是二项分布的实数推广！

多项分布则更进一层，抛硬币时X只能有两种取值，当X有多种取值时，就应该用多项分布建模。

这时参数p变成了一个向量p⃗ =(p1,…,pk)表示每一个取值被选中的概率，那么X~Multinomial(n,p)的PDF为：

伯努利分布最简单，就是抛一次硬币

二项式分布是抛多次硬币，出现n次正面的概率，其概率密度函数图，就是直方图

多项式分布就是抛一个多面体，每个面朝上的概率为pi, 所以p1+p2+...+pk=1, 抛一次的结果是(x11,x12,x13,...,x1k)注意只有一个x1i=1，其他都为0

那么抛n次多面体，就是多项式分布，其中xi表示i面朝上一共出现了xi次