几种 QoS 预测方法
0.问题描述
U = { u 1 , u 2 , … , u m } U = \{u_1, u_2, …, u_m\} U={u1,u2,…,um} 为用户集合
S = { s 1 , s 2 , … , s n } S = \{s_1, s_2, …, s_n\} S={s1,s2,…,sn} 为服务集合
则有 m × n m \times n m×n 的矩阵 V V V 表示服务的 QoS 信息， V i j V_{ij} Vij 表示用户 u i u_i ui 对服务 s j s_j sj 的评价。
在现实环境下，这个矩阵中大部分的元素值都是未知的，因此需要对缺失的值进行预测。
1.NMF 方法 (非负矩阵分解)
方法原理
对任意给定的一个非负矩阵 V V V ,其能够寻找到一个非负矩阵 W W W 和一个非负矩阵 H H H ，满足条件
V ≈ W H V\approx WH V≈WH ，从而将一个非负的矩阵分解为左右两个非负矩阵的乘积。
V ^ = W m × k H k × s min H , W ∥ V − V ^ ∥ 2 s . t . W ≥ 0 , H ≥ 0 \large \hat{V} = W_{m \times k}H_{k \times s} \\ \quad \\ \min_{H, W} \left\| V - \hat{V} \right\| ^2 \quad s.t. \quad W \geq 0, H \geq 0 V^=Wm×kHk×sH,Wmin∥∥∥V−V^∥∥∥2s.t.W≥0,H≥0
k k k一般会选取一个较小的值，满足
( m + n ) k < m n (m+n)k < mn (m+n)k<mn
这时就能对原始矩阵进行降维，得到数据特征的降维矩阵，减少对计算资源的消耗。
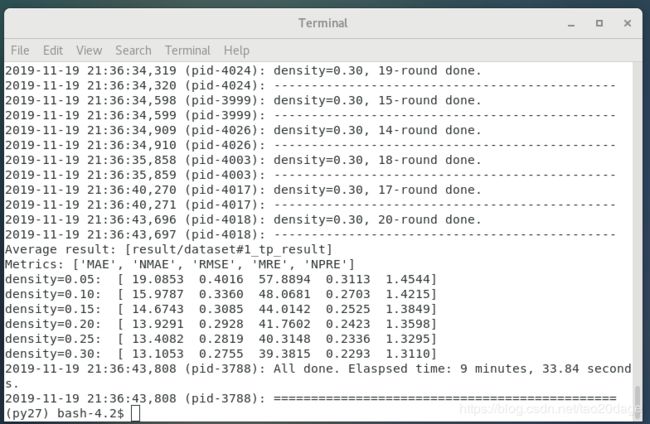
运行结果
- Response Time
- Throughput
2.PMF 方法（概率矩阵分解）
方法原理
这是 SVD 的一种扩展，它基于以下两个假设 1)观测噪声（观测评分矩阵 R R R和近似矩阵 R ^ \hat{R} R^之差）
服从高斯分布, 2)用户属性矩阵 U U U 与服务属性矩阵 V V V 均服从高斯分布, 即
p ( R ∣ U , V ) = N ( R ^ , σ 2 ) p ( U ) = N ( 0 , σ U 2 ) p ( V ) = N ( 0 , σ V 2 ) \large p(R|U, V) = N(\hat{R}, \sigma^2) \\ \quad \\ p(U) = N(0, \sigma_U^2) \\ \quad \\ p(V) = N(0, \sigma_V^2) p(R∣U,V)=N(R^,σ2)p(U)=N(0,σU2)p(V)=N(0,σV2)
从而有
p ( U , V ∣ R ) = p ( R ∣ U , V ) p ( U ) p ( V ) p(U, V|R) = p(R|U,V)p(U)p(V) p(U,V∣R)=p(R∣U,V)p(U)p(V)
两边取对数
l n ( p ( U , V ∣ R ) ) = l n ( p ( R ∣ U , V ) ) + l n ( p ( U ) ) + l n ( p ( V ) ) ln(p(U, V|R)) = ln(p(R|U,V)) + ln(p(U)) + ln(p(V)) ln(p(U,V∣R))=ln(p(R∣U,V))+ln(p(U))+ln(p(V))
利用极大似然估计等方法转换，要求 l n ( p ( U , V ∣ R ) ) ln(p(U, V|R)) ln(p(U,V∣R)) 的最大值，等价于最小化
E ( U , V ) = 1 2 ( R − U T V ) 2 + λ U 2 U T U 2 + λ V 2 V T V 2 = 1 2 ∑ i j I i j ( R i j − U i T V j ) 2 + λ U 2 ∑ i U i T U i 2 + λ V 2 ∑ j V j T V j 2 \large E(U, V) = \frac12 (R-U^TV)^2 + \frac{\lambda_U}{2}U^TU^2 + \frac{\lambda_V}{2}V^TV^2 \\ \quad \\ = \frac12 \sum_{ij} I_{ij}(R_{ij}-U_i^TV_j)^2 + \frac{\lambda_U}{2} \sum_i U_i^TU_i^2 + \frac{\lambda_V}{2} \sum_j V^T_jV^2_j E(U,V)=21(R−UTV)2+2λUUTU2+2λVVTV2=21ij∑Iij(Rij−UiTVj)2+2λUi∑UiTUi2+2λVj∑VjTVj2
（其中 I i j I_{ij} Iij 表示用户 i i i 是否对电影 j j j 评分）
从而可以使用梯度下降法求得 U U U 和 V V V 的值。
###运行结果
- Response Time
- Throughput
3.NIMF (邻域集成矩阵分解)
方法原理
论文 Collaborative Web Service QoS Prediction via Neighborhood Integrated Matrix Factorization
为解决用户个性化的 Web 服务推荐问题，提出了基于邻域的集成矩阵分解方法。该方法通过系统
地融合基于邻域和基于模型的协同过滤方法来探索服务用户过去的 Web 服务使用经验，从而获得
更高的预测精度。
该方法首先计算任意两个用户之间的相似度
P C C ( i , k ) = ∑ j ∈ J ( R i j − R i ˉ ) ( R k j − R k ˉ ) ∑ j ∈ J ( R i j − R i ˉ ) 2 ∑ j ∈ J ( R k j − R k ˉ ) 2 \large PCC(i, k) = \frac{\sum \limits_{j \in J} (R_{ij}- \bar{R_i}) (R_{kj}- \bar{R_k}) }{\sqrt{\sum \limits_{j \in J} (R_{ij}- \bar{R_i})^2} \sqrt{\sum \limits_{j \in J} (R_{kj}- \bar{R_k})^2}} PCC(i,k)=j∈J∑(Rij−Riˉ)2j∈J∑(Rkj−Rkˉ)2j∈J∑(Rij−Riˉ)(Rkj−Rkˉ)
对每个用户 i i i, Top-k(i) 表示和其相似度最高的 k k k 个用户，其邻域用户为
T ( i ) = { k ∣ k ∈ Top-k ( i ) , P C C ( i , k ) > 0 , i ≠ k } \large \mathcal{T}(i) = \{ k|k \in \text{\bf{Top-k}}(i), PCC(i,k)>0, i \neq k \} T(i)={k∣k∈Top-k(i),PCC(i,k)>0,i=k}
与传统的矩阵分解方法相比，该方法的优化目标加入了对邻域用户的考量
L ( R , S , U , V ) = 1 2 ∑ i = 1 m ∑ j = 1 n I i j R ( R i j − α U i T V j + ( 1 − α ) ∑ k ∈ T ( i ) S i k U k T V j ) 2 + λ U 2 U T U 2 + λ V 2 V T V 2 S i k = P C C ( i , k ) ∑ k ∈ T ( i ) P C C ( i , k ) \large \mathcal{L}(R,S,U,V) = \frac12 \sum_{i=1}^m \sum_{j=1}^n I_{ij}^R (R_{ij}- \alpha U_i^TV_j + (1-\alpha ) \sum_{k \in \mathcal{T}(i)} S_{ik} U_k^TV_j)^2 \\ \quad + \frac{\lambda_U}{2}U^TU^2 + \frac{\lambda_V}{2}V^TV^2 \\ \quad \\ S_{ik} = \frac{PCC(i,k)}{\sum \limits_{k \in \mathcal{T}(i)} PCC(i,k)} L(R,S,U,V)=21i=1∑mj=1∑nIijR(Rij−αUiTVj+(1−α)k∈T(i)∑SikUkTVj)2+2λUUTU2+2λVVTV2Sik=k∈T(i)∑PCC(i,k)PCC(i,k)
运行结果
- Response Time
- Throughput
4.NTF (非负张量分解)
方法原理
在论文 Temporal QoS-Aware Web Service Recommendation via Non-negative Tensor Factorization
中，加入了对时间维度的考量，使用了三维的 QoS 张量 Y ∈ R I × J × K \mathcal{Y} \in R^{I \times J \times K} Y∈RI×J×K
在现实世界中， QoS 张量的元素中都是非负的，因此可以对其进行非负张量分解。将其分解成三个
非负的二维矩阵， U ∈ R + I × R Y U\in R_{+}^{I \times R_\mathcal{Y}} U∈R+I×RY, S ∈ R + I × R Y S\in R_{+}^{I \times R_\mathcal{Y}} S∈R+I×RY, T ∈ R + I × R Y T\in R_{+}^{I \times R_\mathcal{Y}} T∈R+I×RY , 并可以通过他们来重构张量 Y Y Y。
优化目标为：
min u r , s r , t r 1 2 ∥ Y i j k − ∑ r = 1 R Y u r ∘ s r ∘ t r ∥ F 2 s . t . u r , s r , t r ≥ 0 \large \min_{u_r, s_r, t_r} \frac12 \left\| \mathcal{Y}_{ijk} - \sum_{r=1}^{R_{\mathcal{Y}}} u_r \circ s_r \circ t_r \right\| ^2_F \quad s.t. \quad u_r, s_r, t_r \geq0 ur,sr,trmin21∥∥∥∥∥∥Yijk−r=1∑RYur∘sr∘tr∥∥∥∥∥∥F2s.t.ur,sr,tr≥0
可以通过求解梯度和乘法更新算法来不断逼近，最后得到近似的矩阵。
运行结果
- Response Time
- Throughput
5.EMF (扩展矩阵分解)
方法原理
该方法和 NIMF 有点类似，但是加上了服务之间的相似考量。
在论文 An Extended Matrix Factorization Approach for QoS Prediction in Service Selection 中，在传
统的矩阵分解方法的基础上通过增加相关用户和相关服务这两个正则项来预测缺失的 QoS 值。
其优化目标为
min U , S L ( R , U , S ) = 1 2 ∑ i = 1 m ∑ j = 1 n I i j ( R i j − U i T S j ) 2 + λ 1 2 ∥ U ∥ F 2 + λ 2 2 ∥ V ∥ F 2 + α 1 2 ∑ i = 1 m ∥ U i − ∑ f ∈ T U ( i ) P U i f ⋅ U f ∥ F 2 + α 2 2 ∑ j = 1 n ∥ S j − ∑ h ∈ T S ( j ) P S j h ⋅ S h ∥ F 2 \large \min_{U,S} \mathcal{L}(R, U, S) = \frac12 \sum_{i=1}^m \sum_{j=1}^n I_{ij} (R_{ij} - U^T_iS_j )^2 + \frac{\lambda_1}{2} \left\|U \right\|^2_F + \frac{\lambda_2}{2} \left\|V \right\|^2_F \\ \quad \\ +\frac{\alpha_1}{2} \sum_{i=1}^m \left\| U_i - \sum \limits_ {f \in \mathcal{TU}(i)} PU_{if} \cdot U_f \right\|^2_F +\frac{\alpha_2}{2} \sum_{j=1}^n \left\| S_j - \sum \limits_ {h \in \mathcal{TS}(j)} PS_{jh} \cdot S_h \right\|^2_F U,SminL(R,U,S)=21i=1∑mj=1∑nIij(Rij−UiTSj)2+2λ1∥U∥F2+2λ2∥V∥F2+2α1i=1∑m∥∥∥∥∥∥∥Ui−f∈TU(i)∑PUif⋅Uf∥∥∥∥∥∥∥F2+2α2j=1∑n∥∥∥∥∥∥∥Sj−h∈TS(j)∑PSjh⋅Sh∥∥∥∥∥∥∥F2
T U ( i ) \mathcal{TU}(i) TU(i) 表示用户 i i i 的基于 Top-k 的相邻用户，矩阵 P U PU PU 表示用户之间的经过归一化后的相似度，
T S ( j ) \mathcal{TS}(j) TS(j) 表示服务 j j j 的基于 Top-k 的相邻服务，矩阵 P S PS PS 表示服务之间的经过归一化后的相似度。
运行结果
- Response Time
- Throughput
