漫步数理统计十五——两个随机变量的分布

接下里我们讨论两个随机变量的例子。连续掷三次硬币并考虑有序数对(前两次 H 的个数，三次中 H 的个数)，其中 H,T 分别表示正面与反面，那么样本空间是 C={c:c=ci,i=1,2,…,8} ，其中 c1 是 TTT ， c2 是 TTH ， c3 是 THT ， c4 是 HTT ， c5 是 THH ， c6 是 HTH ， c7 是 HHT ， c8 是 HHH ，令 X1 ， X2 是两个函数，使得 X1(c1)=X1(c2)=0,X1(c3)=X1(c4)=X1(c5)=X1(c6)=1,X1(c7)=X1(c8)=2 且 X2(c1)=0,X2(c2)=X2(c3)=X2(c4)=1,X2(c5)=X2(c6)=X2(c7)=2,X2(c8)=3
那么 X1,X2 是定义在样本空间 C 上的实值函数，从样本空间映射到有序数对空间

D={(0,0),(0,1),(1,1),(1,2),(2,2),(2,3)}

X1,X2 是定义在样本空间 C 上的两个随机变量，在本例中，这些随机变量的空间是二维集合 D ，它是二维欧几里得空间 R2 的子集，这里 (X1,X2) 是从 C 到 D 的向量，现在我们形式化随机向量的定义。

定义1： (随机向量)给定一个样本空间为 C 的随机试验，考虑两个随机变量 X1,X2 ，对 C 中的每个元素c只分配一个有序数对 X1(c)=x1,X2(c)=x2 ，那么我们称 (X1,X2) 是一个随机向量。 (X1,X2) 的空间是有序数对 D={(x1,x2):x1=X1(c),x2=X2(c),c∈C} 的集合。

我们常用向量符号 X=(X1,X2)′ ，其中 ′ 表示行向量 (X1,X2)′ 的转置。

令 D 是随机向量 (X1,X2) 关联的空间， A 是 D 的一个子集，与随机变量一样我们称为事件 A ，我们想定义事件 A 的概率，用 PX1,X2[A] 表示，同样我们用累加分布函数(cdf)来定义 PX1,X2 ，那么对任意 (x1,x2)∈R2

FX1,X2(x1,x2)=P[{X1≤x}∩{X2≤x2}]

因为 X1,X2 是随机变量，所以上面相加事件中的每个事件都是原始样本空间 C 中的事件，因此上面的表达式是明确的。与随机变量一样，我们可以将 P[{X1≤x1}∩{X2≤x2}] 写成 P[X1≤x1,X2≤x2] ，并且

P[a1<X1≤b1,a2<X2≤b2]=FX1,X2(b1,b2)−FX1,X2(a1,b2)−FX1,X2(b1,a2)+FX1,X2(a1,a2)

因此所有形如 (a1,b1]×(a2,b2] 集合的概率可以用cdf的形式表述出来， R2 中这种形式的集合生成了 R2 子集的博莱尔 σ 域，cdf唯一地确定一个 R2 上的概率，我们常称这种cdf为 (X1,X2) 的联合累积分布函数。

与随机变量一样，我们主要关系两种类型的随机向量，即离散与连续，首先讨论离散情况。

随机向量 (X1,X2) ，如果它的空间 D 是有限的或可数的，那么我们称它是离散随机向量，因此 X1,X2 都是离散的，对于所有的 (x1,x2)∈D ， (X1,X2) 的联合概率质量函数(pmf)定义为

pX1,X2=P[X1=x1,X2=x2]

与随机变量一样，pmf唯一的确定cdf，它也可以用两个性质表征：

(i)0≤pX1,X2(x1,x2)≤1(ii)ΣΣDpX1,X2(x1,x2)=1

对于事件 B∈D ，我们有

P[(X1,X2)∈B]=∑∑BpX1,X2(x1,x2)

例1： 考虑定义在文章开头实例中的离散随机向量 (X1,X2) ，我们可以用下表表示其pmf：

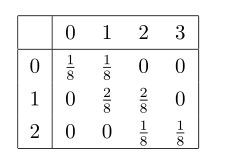
表格横向的 0,1,2,3 表示 X2 的支撑，纵向 0,1,2 表示 X1 的支撑。

这样也便于叙述离散随机向量 (X1,X2) 的支撑，他们是 (X1,X2) 空间中使得 p(x1,x2)>0 的所有点 (x1,x2) ，上面的例子中支撑是由六个点 {(0,0),(0,1),(1,1),(1,2),(2,2),(2,3)} 组成的。

对于空间为 D 的随机向量 (X1,X2) ，如果它的cdf FX1,X2(x1,x2) 是连续的，那么我们称该随机向量是连续的。在以后的文章中，有cdf的连续随机向量用非负函数的积分表示，即对于所有的 (x1,x2)∈R2,FX1,X2(x1,x2) 可以表示成

FX1,X2(x1,x2)=∫x1−∞∫x2−∞fX1,X2(w1,w2)dw1dw2

我们称被积部分为 (X1,X2) 的联合概率密度函数(pdf)，对于 fX1,X2(x1,x2) 连续的点，我们有

∂2FX1,X2(x1,x2)∂x1∂x2=fX1,X2(x1,x2)

pdf基本可有两个性质表征：

(i)fX1,X2(x1,x2)≥0(ii)∫∫DfX1,X2(x1,x2)dx1dx2=1

对于事件 A∈D ，我们有

P[(X1,X2)∈A]=∫∫AfX1,X2(x1,x2)dx1dx2

注意 P[(X1,X2)∈A] 仅仅是集合 A 上曲面 z=fX1,X2(x1,x2) 下方的体积。

注： 与单随机变量一样，我们经常省略cdf，pdf与pmf中的下标 (X1,X2) ，我们也常用符号 f12 而不是 fX1,X2 。除了 (X1,X2) ，我们也常用 (X,Y) 表示随机向量。

例2： 令

f(x1,x2)={6x21x200<x1<1,0<x2<1elsewhere

是两个连续随机变量 X1,X2 的pdf，那么我们有

P(0<X1<34,13<X2<2)=∫21/3∫3/40f(x1,x2)dx1dx2=∫11/3∫3/406x21x2dx1dx2+∫21∫3/400dx1dx2=38+0=38

注意这个概率是矩形集合 {(x1,x2):0<x1<34,13<x2<1}∈R2 上曲面 f(x1,x2)=6x21x2 下的体积。

对于连续随机向量 (X1,X2) ， (X1,X2) 的支撑包含所有 f(x1,x2)>0 的点，我们用 S 表示随机向量的支撑，与单变量一样 S⊂D 。

对于 R2 上pdf fX1,X2(x1,x2) 的定义，我们通过将其他地方设为零进行扩展，这样的话就可以避免麻烦的 D ，这样的话我们就能将

∫∫DfX1,X2(x1,x2)dx1dx2

替换为

∫∞−∞∫∞−∞fX1,X2(x1,x2)dx1dx2

离散情况同样如此，可将

∑∑DpX1,X2(x1,x2)

替换为

∑x2∑x1pX1,X2(x1,x2)

最后如果一个或多个变量的pmf或者pdf已经显示的给定，那么通过观察就能看出随机变量是离散还是连续类型，例如显然

p(x,y)={94x+y0x=1,2,3,…,y=1,2,3,…elsewhere

是两个离散变量 X,Y 的pmf，而

f(x,y)={4xye−x2−y200<x<∞,0<y<∞elsewhere

显然是两个连续随机变量 X,Y 的pdf。

令 (X1,X2) 是随机向量，那么 X1,X2 每一个都是随机变量，我们用 (X1,X2) 的联合分布形式得到他们的分布，回忆一下定义在 x1 处 X1 cdf的事件是 {X1≤x1} ，然而

{X1≤x1}={X1≤x1}∩{−∞<X2<∞}={X1≤x1,−∞<X2<∞}

取概率得对于所有的 x1∈R

FX1(x1)=P[X1≤x1,−∞<X2<∞]

将上式重写成 FX1(x1)=limx2↑∞F(x1,x2) ，由此我们得到cdf之间的关系，根据 (X1,X2) 是离散的或连续的，我们可以将其扩展到pmf或者pdf。

首先考虑离散情况，令 DX1 是 X1 的支撑，对于 x1∈DX1 ，上式等价于

FX1(x1)=∑w1≤x1∑−∞<x2<∞pX1,X2(w1,x2)=∑w1≤x1⎧⎩⎨∑x2<∞pX1,X2(w1,x2)⎫⎭⎬

根据cdf的唯一性，括号中的量肯定是 X1 在 w1 处的pmf；即对于所有的 x1∈DX1

pX1(x1)=∑x2<∞pX1,X2(x1,x2)

注意，为了找出 X1 是 x1 的概率，保持 x1 不变然后在所有 x2 上求和 pX1,X2 ，如下表所示。表的最后一行是 X2 的pmf，最后一列是 X1 的pmf，一般而言，因为这些分布记录在表的边缘，所以我们常称他们为边缘pmf。

例3： 考虑一个随机试验，从包含10个同样大小球的盒子中随机抽一个球，每个球上标有数字对，一个为 (1,1) ，一个为 (2,1) ，两个为 (3,1) ，一个为 (1,2) ，两个为 (2,2) ，三个为 (3,2) 。令随机变量 X1,X2 分别表示有序对的第一个与第二个数，那么 X1,X2 的联合pmf p(x1,x2) 如下表所示，其中 p(x1,x2) 在其他地方等于零。

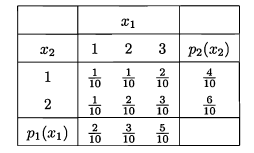
每行与每列的联合概率进行相加，这些边缘的和分别给出了 X1,X2 的边缘概率密度函数，注意为了求出他们我们没必要知道 p(x1,x2) 。

接下来考虑连续情况，令 DX1 表示 X1 的支持，对于 x1∈DX1

FX1=∫x1−∞∫∞−∞fX1,X2(w1,x2)dx2dw1=∫x1−∞{∫∞−∞fX1,X2(w1,x2)dx2}dw1

根据cdf的唯一性，括号中的量一定是 X1 在 w1 处的pdf；即对所有 x1∈D_{X_1}

fX1(x1)=∫∞−∞fX1,X2(x1,x2)dx2

因此对于连续情况， X1 的pdf通过积分 x2 得到，同样的 x2 的pdf可以通过积分 x1 得到。

例4： X1,X2 的联合pdf为

f(x1,x2)={x1+x200<x1<1, 0<x2<1elsewhere

X1 的边缘pdf为

f1(x1)=∫10(x1+x2)dx2=x1+12,0<x1<1

其他地方为零， X2 的边缘pdf为

f1(x1)=∫10(x1+x2)dx2=12+x2,0<x2<1

其他地方为零。像 P(X1≤12) 的概率既可以从 f1(x1) 也可以从 f(x1,x2) 中计算得到，因为

∫1/20∫10f(x1,x2)dx2dx1=∫1/20f1(x1)dx1=38

然而为了求出像 P(X1+X2≤1) ，我们必须用联合pdf f(x1,x2) ，如下所示：

∫10∫1−x10(x1+x2)dx2dx1=∫10[x1(1−x1)+(1−x1)22]dx1=∫10(12−12x21)dx1=13

这个概率就是集合 {(x1,x2):0<x1,x1+x2≤1} 上曲面 f(x1,x2)=x1+x2 下的体积。

(X1,X2) 是一个随机向量， Y=g(X1,X2) 是某个实值函数，即 g:R2→R ，那么 Y 是一个随机变量且通过 Y 的分布可以确定它的期望。

假设 (X1,X2) 是连续类型，那么如果

∫∞−∞∫∞−∞|g(x1,x2)|fX1,X2(x1,x2)dx1dx2<∞

则 E(Y) 存在，

E(Y)=∫∞−∞∫∞−∞g(x1,x2)fX1,X2(x1,x2)dx1dx2

类似的，如果 (X1,X2) 是离散的，那么如果

∑x1∑x2|g(x1,x2)|pX1,X2(x1,x2)dx1dx2<∞

则 E(Y) 存在，

E(Y)=∑x1∑x2g(x1,x2)pX1,X2(x1,x2)dx1dx2

现在我们说明 E 是一个线性运算。

定理1： 令 (X1,X2) 是一个随机向量， Y1=g1(X1,X2),Y2=g2(X1,X2) 是随机变量，其期望存在，那么对任意实数 k1,k2

E(k1Y1+k2Y2)=k1E(Y1)+k2E(Y2)

证明： 我们证明连续情况。 k1Y1+k2Y2 期望值的存在性直接从三角不等式以及积分的线性可以求出，即

∫∞−∞∫∞−∞|k1g1(x1,x2)+k2g1(x1,x2)|fX1,X2(x1,x2)dx1dx2≤|k1|∫∞−∞∫∞−∞|g1(x1,x2)|fX1,X2(x1,x2)dx1dx2+|k2|∫∞−∞∫∞−∞|g2(x1,x2)|fX1,X2(x1,x2)dx1dx2<∞

利用积分的线性可得

E(k1Y1+k2Y2)=∫∞−∞∫∞−∞[k1g1(x1,x2)+k2g2(x1,x2)]fX1,X2(x1,x2)dx1dx2=k1∫∞−∞∫∞−∞g1(x1,x2)fX1,X2(x1,x2)dx1dx2+k2∫∞−∞∫∞−∞g2(x1,x2)fX1,X2(x1,x2)dx1dx2=k1E(Y1)+k2E(Y2)