马尔科夫模型

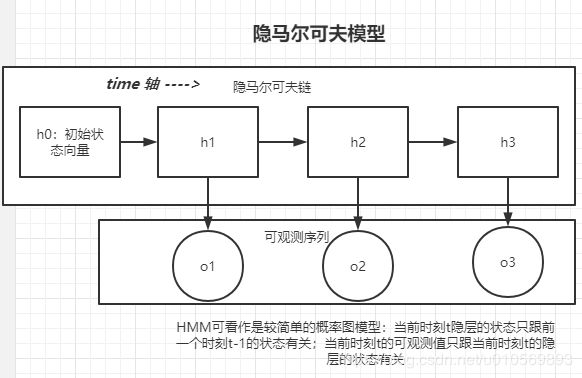
隐马尔科夫模型

HMM的定义

​ 隐马尔可夫模型是统计模型，它用来描述一个含有隐含未知参数的马尔科夫过程。其难点是从可观测的参数中确定该过程的隐含参数，然后利用这些隐含的函数来做进一步的分析，例如模式识别。

​ 隐马尔可夫模型是马尔科夫模型中的一种，他的状态不能直接观测到，但是能够通过可观测向量观测到，每个观测向量都是通过某些概率密度分布表现为各种状态，每个观测向量是由一个具有相应概率密度分布的状态序列产生。所以，隐马尔可夫模型是一个双重随机过程-----具有一定状态数的隐马尔可夫链和显示随机函数集。

​ 隐马尔可夫HMM可以看作是最简单的动态贝叶斯网络。

​ 在马尔科夫模型中状态时不能直接可见的，但是输出依赖于该状态下，是可见的。

HMM的应用场景

现实生活中有这样一类随机现象，在已知现有情况的条件下，未来时刻的情况只跟现在有关，而与遥远的过去并无直接的关系；

比如，天气预测，如果我们知道“晴天、多云和雨天”之间的转换矩阵，那么今天是晴天，我们就能腿短明天是各个天气的概率，接着后天的天气可由明天的天气进行计算，这类问题可以用马尔科夫模型来描述。

进一步的，如果我们并不知道今天的天气属于什么状况，我们只知道今明后三天的水藻的干燥湿润状态，因为水藻的状态和天气有关，我们想通过水藻来推测这三天的真正天气会是什么，这时可以用隐马尔可夫模型。

HMM模型的本质是从观察的参数中获取隐含的参数信息，并且前后之间的特征会存在部分的依赖关系影响。

我们如何从中文分词的角度来理解HMM：根据可观测状态序列来找到一个最可能的隐藏状态序列

中文分词，就是给一个汉语句子作为输入，以“BEMS”组成的序列串作为输出，再进行切词，得到输入句子的划分。其中B代表词语的起始字，M代表词语的中间字，E代表词语的结束字，S代表单字成词。

例如：

输入：小明硕士毕业于中国科学院计算所
得到BEMS组成的序列：BEBEBMEBEBMEBES
因为句尾只可能是E或者S，所以得到切词方式为：BE/BE/BME/BE/BME/BE/S
进而得到中文句子的切词方式为：小明/硕士/毕业于/中国/科学院/计算/所

这是一个HMM问题，因为你想得到每个字的位置，但是看到的只是这些汉字，需要通过汉字来推出每个字在词语中的位置，并且每个字属于什么状态还跟它之前的字有关。

此时，我们需要根据可观测状态序列找到一个最可能的隐藏状态序列

HMM可以用五个元素来描述，即2个状态集和3和概率矩阵

1）隐含状态S

​ 这些状态之间满足马尔科夫性质，是马尔科夫模型中实际隐含的状态，这些状态通常无法直接观测而得到。

2）可观测状态O

​ 在模型中跟隐藏状态直接相连，可通过观测直接得到。（可观测状态的数目不一定跟隐藏状态的数目一致）

3）初始状态转移矩阵 π

​ 表示隐藏状态在初始时刻t=1的概率矩阵

4）隐藏状态转移概率矩阵A

​ 表示隐藏层的各个状态之间的转移概率，Aij = P(sj|si)表示前一个时刻t-1的隐藏状态下si，t时刻的状态sj的概率

5）观测状态转移概率矩阵B

​ 表示从隐藏状态到观测状态的概率， Bij = P(oi|sj), 1<=i<=M, 1<=j<=N, 表示在t时刻，隐藏状态sj的条件下，观测状态oi的概率

​ 综上，状态转移概率矩阵A和初始状态概率向量π确定了隐藏的马尔科夫链，生成不可观测的隐藏状态序列，观测概率矩阵B确定了如何从隐藏状态生成可观测序列。

​ 一般可用λ=(A,B,π)三元组来简洁表示一个HMM模型；HMM模型是标准马尔科夫模型的扩展，添加了可观测状态集合和这些集合与隐含状态之间的概率关系。

通过上面的例子，我们可以知道HMM的5个要素：

观测序列-O : 小明硕士毕业于中国科学院计算所

状态序列-S：BEBEBMEBEBMEBES

初始状态概率向量-π ：句子的第一个字属于{B（begin)、E(end)、M(middle)、S(single)}这四种状态的概率

状态转移概率矩阵-A：如果前一个字位置是B，那么后一个字位置是BEMS的概率各是多少？

观测概率矩阵-B：在状态B的条件下，观测值是“耀”的概率，取对数后是-10.460

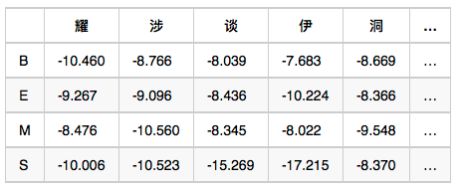
备注：示例数值是对概率值取对数后的结果，为了将概率相乘的计算变成对数相加，其中-3.14e+100作为负无穷，就是对应的概率值是0

HMM的两个基本假设

1）马尔科夫假设

​ 假设隐藏状态的马尔科夫链在任意时刻t 的状态只依赖于其前一个时刻的状态，与其他时刻的状态无关

p(qt|qt-1, ot-1, ..., q1, o1) = p(qt|qt-1), t=1,2,...,T

2）观测独立性假设

​ 任意时刻的观测只依赖于该时刻的马尔科夫链的状态，与其他的观测和状态无关

P(ot|qT, oT, qT-1, oT-1, ..., q1, o1) = P(ot|qt)

根据贝叶斯公式可得到下面的公式：
P(s1,s2,s3,...|o1,o2,o3,...) = P(o1,o2,o3,...|s1,s2,s3,...)*P(s1,s2,s3,...)
根据上面的两个假设来进一步简化上述公式：
P(o1, o2, o3, ...|s1, s2, s3, ...) = P(o1|s1)*P(o2|s2)*P(o3|s3)...
P(si|si-1,si-2,...,s2,s1) = P(si|si-1)

HMM可以解决的问题

1）评估问题

给定观测序列O（o1,o2,…,ot)和模型的参数λ=(A,B,π) ,怎样有效计算某一个观测序列的概率，进而可对该HMM模型进行评估。例如：有一些模型参数各异的HMM，给定观测序列O,我们想知道哪个HMM模型是最可能生成该观测序列。通常我们利用formard算法分别计算每个HMM产生给定观测序列的O的概率，然后从中选择最优的HMM

这类评估问题的一个经典例子就是语音识别。在描述语音识别的隐马尔可夫模型中，每个单词生成一个对应的HMM，每个观测序列由一个单词的语音构成，单词的识别是通过评估进而选出最有可能产生观测序列所代表的的读音的HMM而实现的

2）解码问题

给定一个观测序列O和模型的参数λ=(A,B,π) ，怎样寻找某种意义上的最优的隐藏状态序列。在这类问题中，我们感兴趣的是马尔科夫模型中的隐藏状态，这些隐藏状态不能直接观测但是却更有价值，通常利用Viterbi算法来寻找。

公式推导：

Viterbi算法实际上解决P（I|O,λ )最大化的问题，给定观测序列求其最可能对应的状态序列。算法首先需要导入两个变量δ和ψ。 δ是在时刻t状态为i的所有单个路径（i1, i2, …, it)中概率的最大值：

由定义可得变量 δ的递推公式：

算法在设定初始值δ1(i)=πibi(oi)之后就不断迭代，终止条件是：

3）学习问题

即HMM的模型参数λ=(A,B,π) 未知，如何调整这些参数使得观测序列O的概率尽可能的大。即怎样调整模型参数λ=(A,B,π) 使观测序列的O的概率最大

中文分词属于解码问题

我们希望找到s_1, s_2, s_3, … 使P(s_1,s_2,s_3,…|o_1,o_2,o_3,…)达到最大

意思是，当我们观测到语音信号o_1, o_2, o_3, … 时，我们要根据这组信号推测发送出的句子s_1,s_2, s_3,…,显然，我们应该在所有可能的句子中找出最有可能的一个。

举个例子：

已知隐马尔科夫模型λ=(A,B,π) ，如下：

观测序列O={红、白、红}， 想要求状态序列S

需要定义两个变量：

weight[3][3]:行3是状态数（1,2,3），列3是观测值个数{红、白、红}。意思是，在时刻t 状态为i的所有单个路径中的概率最大值
path[3][3]:意思是在时刻t状态为i的所有单个路径中概率最大的那个路径，它的第t-1个节点是什么。比如path[0][2]=1，则代表weight[0][2]取到最大时，前一个时刻的状态是1 

1）初始化：

t=1时，分别是在状态1,2,3的条件下观测到的概率计算如下：

状态值	红
1	0.2*0.5=0.1
2	0.4*0.4=0.16
3	0.4*0.7=0.28(最大)

2）递归

	t=1红	t=2白	t=3红
1	0.2*0.5=0.1	0.1 * 0.5 * 0.5 = 0.025 0.16 * 0.3 * 0.5 = 0.024 0.28 * 0.2 *0.5 = 0.028 (max)	max = 0.00756 0.028 * 0.5 * 0.5 = 0.0098 0.0504 * 0.3 * 0.5 = 0.00756(max) 0.042 * 0.2 * 0.5 = 0.00588
2	0.4*0.4=0.16	0.1 * 0.2 * 0.6 =0.012 0.16 * 0.5 * 0.6=0.048 0.28 * 0.3 * 0.6=0.0504(max)	0.028 * 0.2 * 0.4 = 0.00224 0.0504 * 0.5 * 0.4 = 0.01008（max) 0.042 * 0.3 * 0.4 = 0.00504
3	0.4*0.7=0.28	0.1 * 0.3 * 0.3 =0.009 0.16 * 0.2 * 0.3=0.0096 0.28 * 0.5 * 0.3=0.042(max)	0.028 * 0.3 * 0.7 = 0.00588 0.0504 * 0.2 * 0.7 = 0.007056 0.042 * 0.5 * 0.7 = 0.0147(max)

path:

	t=1红	t=2白	t=3红
1	0	3	2
2	0	3	2
3	0	3	3

3）终止

在t=3时的最大概率P = 0.0147,相应的最有路径是终点是i_3 = 3

4)回溯

由最优路径的终点3开始，向前找到之前时刻的最优点：

在t=2时， 因i_3 = 3,状态3的最大概率p=0.0147, 来源于状态3， 所以i_2 = 3

在t=1时，因i_2=3,状态3的最大概率p=0.042, 来源于状态3, 所以i_1 = 3

最后得到的最优路径是I = (i_1, i_2, i_3) = (3,3,3)

Viterbi求解

经过这个算法后，会得到两个矩阵weight和path:

二维数组weight[4][15], 4是状态数（0:B,1:E, 2:M, 3:S)，15是输入的句子的字数。比如：weight[0][2]代表状态B的条件下，出现"硕"字的可能性。

二维数组path[4][15],4是状态数(同上)，15是输入句子的字数。比如path[0][2]代表weight[0][2]取到最大值时，前一个字的状态， 比如path[0][2]=1，代表wright[0][2]取最大值时，前一个字“明"的状态是E。记录前一个字的状态是为了使用Viterbi算法计算完整个weight[4][15]后，能对输入的句子从右向左地回溯回来，找出对应的状态序列

path[4][15],4是状态数(同上)，15是输入句子的字数。比如path[0][2]代表weight[0][2]取到最大值时，前一个字的状态， 比如path[0][2]=1，代表wright[0][2]取最大值时，前一个字“明"的状态是E。记录前一个字的状态是为了使用Viterbi算法计算完整个weight[4][15]```后，能对输入的句子从右向左地回溯回来，找出对应的状态序列