信用违约判断逻辑回归实例--LogisticRegression
1、目标
根据已知用户违约数据,预测用户是否违约。
2、逻辑回归模型知识准备
模型目标: 分类0-1, 得到指定属性归类为1有多大概率,归类为0 有多大概率。--用于分类。
适用: 经典二分类问题
二元逻辑回归:回归结果分类0-1两类;
多元逻辑回归:回归结果分类两类以上。
逻辑回归推导原理
(参考了各种资料后纯个人理解个人认为已经是很通俗的白话文,可能中间与官放的原理讲解会有些出入,此处经过了个人的理解翻译,主要帮助了解一下原理,需要真正了解所有推导过程以及数学公式,还是需要另外搜一下其他大神的讲解哦,菜鸟起步望多包涵,多指教):
①线性回归推导原理:
逻辑回归与线性回归有很多相似之处,线性回归——已知多个自变量矩阵X,通过寻求一组最优的参数矩阵θ,建立一个回归方程(模型),该模型直线将尽可能多的已知的点-相当于Y【Hθ(X)】值。
A). 理论完美线性模型经过多有所有y点>>>Hθ(X)=θ.T * X
(相当于多元方程组 y=ax0+bx1+cx2 ,abc组合就是θ参数组合-θ.T为矩阵转置,X0等变量就是一列一列的矩阵)
B). 实际是不可能画出完全拟合(相当于穿过的意思)所有已知的y值点,那么求出来的模型和时间y值必会有一个误差那么
实际y值 = 预测y值 +误差 =>y=Hθ(X)+损失值=>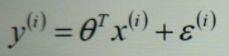
C). 我们的目标是经过尽可能多的点,那么我们希望误差值就是越小越好,误差值用已知的x、y值替代,求误差极小值,
经过一系列的各种复杂的数据公式原理用似然以及求导等推导【普通最小二乘法】,
#线性回归实际解决中:因求矩阵逆有条件限制,当逆矩阵不存在则找不出精确的θ,故目前θ一般用梯度机器迭代(理解即可:在求误差最小值的过程中,通过设置θ初始组合和自定义距离以及迭代次数等,求一段距离范围内的最大/最小值,每次迭代不满足一定条件就更新θ值在继续直到满足条件。)的方式。在Python中只要学会调用模型包进行训练即可,推导原理可以帮助更加深入的理解模型的出生背景。
①逻辑回归推导原理:
(逻辑回归看了很多的推导的原理,总是有种说不出的的感觉,感觉比线性回归原理好难理解好多- _ -||)
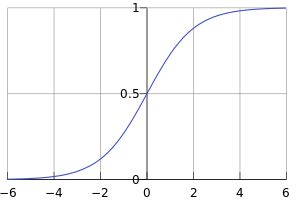
逻辑回归--求概率=>》实际上是预测z=某个值的时候概率有多大,概率大于0.5时分类为1,小与0.5时分类为0,z相当于线性回归的Hθ(X)
a). 先了解一下sigmoid函数,横坐标【负无穷~正无穷】,这里个人理解是已知一堆已知变量,构造出一个线性回归预测一个
b). 求解方法与线性回归基本相似,均是寻找一组最优的θ值,θ和X组合求出来的概率最大化。而此处,θ的求解应用了梯度
下降法。目前求解过程有用梯度下降法、随机梯度上升、改进梯度上升等方法。这些方法再Python的包里面均已经包装
好,调用就行啦,如果感兴趣的童鞋,建议还是去找纯原理的文章学习观摩一下,个人统计学和数学学得不好,纯属个
人理解大概原理,使用的都是先人研究的成果。
逻辑回归Python实例
数据源:
逻辑回归过程:①源数据保留最后20条记录做为测试集,其他数据作为训练集,求分类模型
②源数据先全部采用随机逻辑回归模型,筛选出于违约相关性最大的属性,再用这些属性值进行①分类;
代码如下:
#!/usr/bin/evn python # -*-coding:utf8 -*- import pandas as pd # #初始化输入文件 inputfile = 'F:\\kettle\\tbsales\\pyhon_seana\\chapter5\\demo\\data\\bankloan.xls' outputfile = 'F:\\kettle\\tbsales\\pyhon_seana\\testresult\\bankloan_test2.xls' # data = pd.read_excel(inputfile,sheet_name='bankloan',header=0) x = data.iloc[:,:8] #获取所有行,8列数据([m:n] 表示索引编号m开始取,找到索引n,但是不包含索引n对应的数据),并生成一个矩阵。 y = data.iloc[:,8]#.as_matrix() #获取所有行,编号=8的列数据,第9列,并生成一个矩阵。 x1 = data.iloc[:-20,:8].as_matrix() y1 = data.iloc[:-20,8].as_matrix() x1_test = data.iloc[-20:,:8].as_matrix() y1_test = data.iloc[-20:,8].as_matrix() def logic_train(a, b, a_test, b_test): from sklearn.linear_model import LogisticRegression as LR from sklearn.metrics import classification_report,confusion_matrix lr = LR(penalty='l2',solver='newton-cg',multi_class='ovr') #建立逻辑回归模型 lr.fit(a, b) #用筛选后的特征数据训练模型 pred_test = lr.predict(a_test) print(u'逻辑回归模型训练结束') print('模型的准确率为:{}'.format(lr.score(a,b))) print(classification_report(b_test, pred_test)) print('y_test: ', b_test) print('pred_test:', pred_test) def logic_choose_train(a, b): ''' 先筛选特征,再进行逻辑回归分析 :param a: x :param b: y :return: 返回回归结果以及模型评价 ''' from sklearn.linear_model import RandomizedLogisticRegression as RLR #随机逻辑回归模型,专门用来筛选特征变量 RLR = RLR() RLR.fit(a, b) RLR.get_support() #获取特征筛选结果,也可以通过.scroes_方法获取各特征的分数 # print(RLR.scores_) # datax = a.iloc[:,:8] print('有效特征为:{}'.format(','.join(a.columns[RLR.get_support()]))) x = a[a.columns[RLR.get_support()]].iloc[:-20,:] y = b.iloc[:-20].as_matrix() x_test = a[a.columns[RLR.get_support()]].iloc[-20:,:] y_test = b.iloc[-20:].as_matrix() logic_train(x, y, x_test, y_test) logic_choose_train(x,y) print('我是分割线'.center(50,'=')) logic_train(x1,y1,x1_test,y1_test)运行结果:
模型评价的含义:
#from sklearn.metrics import confusion_matrix
#tn, fp, fn, tp = confusion_matrix(y_test, y_pred=pred_test).ravel()
不同的模型但看一个综合评分是片面的,需要结合业务去看,比如看待银行违约的行为,要尽可能的规避违约的风险,那么我们的模型出来的预测结果,宁愿错判段不违约的为违约,进行用户违约前做预警处理,也不愿放过每一个违约的可能,一旦用户违约就会对银行造成损失,所以实际模型中需要深刻的理解混淆矩阵的意义,模型才是能是最适合业务的。
TP: 预测为1(Positive),实际也为1(Truth-预测对了)
TN: 预测为0(Negative),实际也为0(Truth-预测对了)
FP: 预测为1(Positive),实际为0(False-预测错了)
FN: 预测为0(Negative),实际为1(False-预测错了)
(P=1,N=0,T=分类正确,F分类错误)
总的样本个数为:TP+TN+FP+FN。
准确率Accuracy :
(预测正确的样本数)/(总样本数)=(TP+TN)/(TP+TN+FP+FN)
精度/查准率Precision:
(预测为1且正确预测的样本数)/(所有预测为1的样本数) = TP/(TP+FP)
所有预测的1中,正确的预测的比例
查全率Recall :
(预测为1且正确预测的样本数)/(所有真实情况为1的样本数) = TP/(TP+FN)
所有真正的1中,预测正确了的比例
F1 :
2*(Precision*Recall)/(Precision+Recall)
综合Precision/Recall