MNIST手写数字的识别——CNN篇

这里贴一个用nolearn，lasagne训练CNN的例子，数据集嘛，当然是MNIST咯，keras暂时还没研究过，但nolearn训练CNN真的炒鸡炒鸡方便啊

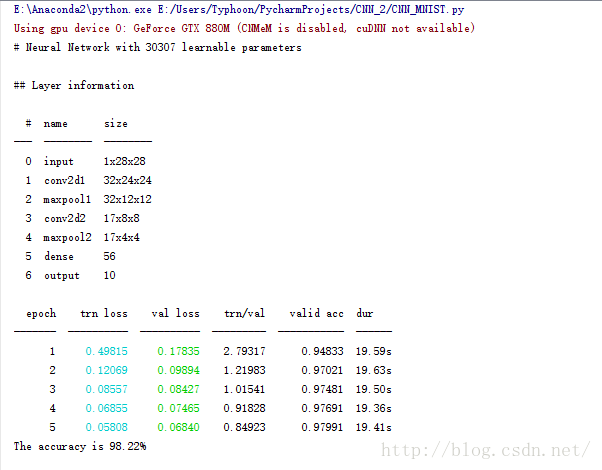
这里简单说下CNN的结构，首先是输入层，是一个1*28*28的图像矩阵，用32个5*5*1的滤波器去虑，得到32*24*24的hidden layer，然后对这个东西进行（2,2）的maxpool，结果是32*12*12的hidden layer，然后在用17个32*5*5的滤波器去过滤，得到17*8*8的hidden layer，然后在进行（2,2）的maxpool，得到17*4*4的hidden layer。先把这个hidde layer投射到56个神经元的hidden layer（这里就像普通的神经网络了，所以叫dense layer），最后是输出层，输出有10个，用softmax进行判定。这里和Coursera上的AndrewNg老师的作业不太一样，因为作业中是用10个2分的logistic regression classifier进行分类的，所以对于单个training example，其造成的cost 是10部分的相加，但对于softmax，单个training example的cost直接就是一个东西。

# coding=utf-8
# 按别人的改的
# 版权未知，盗版不究
# typhoonbxq
# the University of Hong Kong

from urllib import urlretrieve
import cPickle as pickle
import os
import gzip
import numpy as np
# import theano
import lasagne
import csv

from lasagne import layers
from lasagne.updates import nesterov_momentum
from nolearn.lasagne import NeuralNet

def load_dataset():
    url = 'http://deeplearning.net/data/mnist/mnist.pkl.gz'
    filename = 'mnist.pkl.gz'
    if not os.path.exists(filename):
        print("Downloading MNIST dataset...")
        urlretrieve(url, filename)
    with gzip.open(filename, 'rb') as f:
        data = pickle.load(f)
    X_train, y_train = data[0]
    X_val, y_val = data[1]
    X_test, y_test = data[2]
    X_train = X_train.reshape((-1, 1, 28, 28))
    X_val = X_val.reshape((-1, 1, 28, 28))
    X_test = X_test.reshape((-1, 1, 28, 28))
    y_train = y_train.astype(np.uint8)
    y_val = y_val.astype(np.uint8)
    y_test = y_test.astype(np.uint8)
    return X_train, y_train, X_val, y_val, X_test, y_test
X_train, y_train, X_val, y_val, X_test, y_test = load_dataset()

# Set the parameters for the CNN
net1 = NeuralNet(
    layers=[('input', layers.InputLayer),
            ('conv2d1', layers.Conv2DLayer),
            ('maxpool1', layers.MaxPool2DLayer),
            ('conv2d2', layers.Conv2DLayer),
            ('maxpool2', layers.MaxPool2DLayer),
           # ('dropout1', layers.DropoutLayer),
            ('dense', layers.DenseLayer),
            #('dropout2', layers.DropoutLayer),
            ('output', layers.DenseLayer),
            ],
    # input layer
    input_shape=(None, 1, 28, 28),
    # layer conv2d1
    conv2d1_num_filters=32,
    conv2d1_filter_size=(5, 5),
    conv2d1_nonlinearity=lasagne.nonlinearities.rectify,
    conv2d1_W=lasagne.init.GlorotUniform(),
    # layer maxpool1
    maxpool1_pool_size=(2, 2),
    # layer conv2d2
    conv2d2_num_filters=17,
    conv2d2_filter_size=(5, 5),
    conv2d2_nonlinearity=lasagne.nonlinearities.rectify,
    # layer maxpool2
    maxpool2_pool_size=(2, 2),
    # dropout1
    #dropout1_p=0.5,
    # dense
    dense_num_units=56,
    dense_nonlinearity=lasagne.nonlinearities.rectify,
    # dropout2
    #dropout2_p=0.5,
    # output
    output_nonlinearity=lasagne.nonlinearities.softmax,
    output_num_units=10,
    # optimization method params
    update=nesterov_momentum,
    update_learning_rate=0.01,
    update_momentum=0.9,

# Below is a very important parameter, increasing max_epochs will increase the prediction accuracy
# I suggest this is the maximum of the turn for which we update the parameters
# I remember when training a CNN, we limit the traing time

    max_epochs=5,
    verbose=1,
    )
# Train the network
nn = net1.fit(X_train, y_train)

preds = net1.predict(X_test)

l = len(preds)
count = 0

f0 = open('F:\\result.csv','wb')
f1 = csv.writer(f0)


Y = y_test.tolist()
for i in range(0,l):
    f1.writerow([Y[i],preds[i]])
    if(preds[i] == y_test[i]):
        count = count + 1
acc = count * 100.0 / l
print "The accuracy is %.2f%%"%(acc)
f0.close()

然后贴个运行的结果，

可以看出来，正确率是非常高的，这说明……（进入实验报告模式）

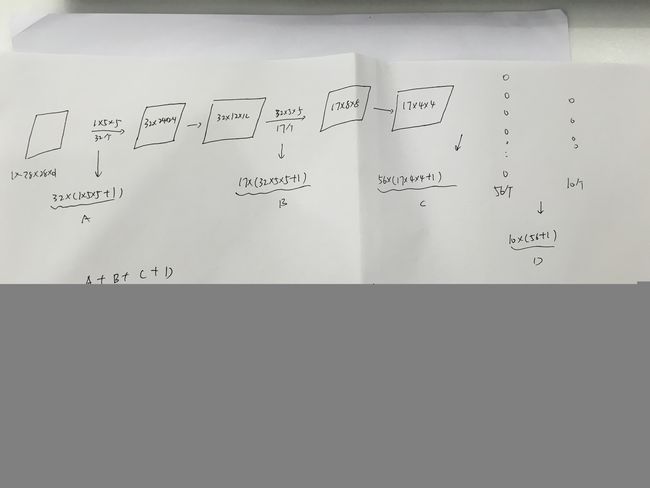
最后我想贴一张纸证明这个30307是怎么计算的，也算是一个基本功吧。