数据分析与挖掘：热水器用户行为分析与事件识别

1. 背景与挖掘目标

• 项目为《Python 数据分析与挖掘实战》第 10 章：家用电器用户行为分析与事件识别。书中给出了原始数据，以及各项属性的构建说明及公式，但并没有给出属性构建的实现方法以及代码。
• 我们的目标为根据书中的原始数据和属性构造说明，利用 Python 进行数据处理，构造各种属性，然后根据各项属性进行事件识别。
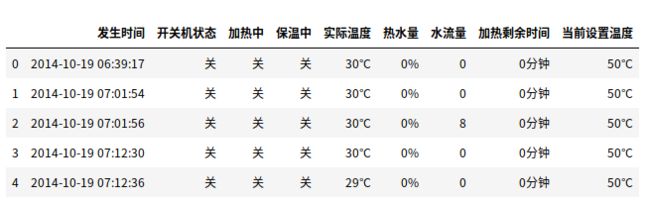
• 原始数据集格式如下图所示：
  

2. 分析方法与过程

• 分析步骤主要有：数据探索，数据预处理，模型构建，模型检验等

2.1 数据探索

• 探索用户用水停顿时间分布，探究划分一次用水事件的时间间隔阈值
• 代码如下：

'''数据探索'''
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib notebook    # 在jupyter notebook 中显示图片
# 载入数据
inputfile = 'chapter10/demo/data/original_data.xls'
data = pd.read_excel(inputfile)
# 用水停顿事件间隔的分布情况
# 用水停顿事件间隔 = 一条水流量不为0的记录时间 - 下一条水流量不为0的记录时间
data['发生时间'] = pd.to_datetime(data['发生时间'], format='%Y%m%d%H%M%S')    # 转换为 Datetime
use_water = data[data['水流量'] != 0]    # 只保留水流量不为0的部分
use_diff = use_water['发生时间'].diff()[1:] / np.timedelta64(1, 'm')         # diff() 计算出来的为 ns，转换为 min
space = [0, 0.1, 0.2, 0.3, 0.5, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, use_diff.max()+1]
labels = ['0~0.1', '0.1~0.2', '0.2~0.3', '0.3~0.5', '0.5~1', '1~2', '2~3', '3~4', '4~5', '5~6', '6~7', '7~8',
         '8~9', '9~10', '10~11', '11~12', '12~13', '13 以上']
time_table = pd.value_counts(pd.cut(use_diff, space, right=False, labels=labels)).sort_index()    # 分箱，计数，按索引排序
time_table.index.name = '频数'
# 绘制用水停顿时间帕累托图
plt.rcParams['figure.constrained_layout.use'] = True    # 自动调整位置
plt.rcParams['font.sans-serif'] = ['SimHei']    # 显示中文
ax = time_table.plot(kind='bar')
ax.set_xlabel('区间')
ax.set_ylabel('频率')
p = 1.0 * time_table.cumsum() / time_table.sum()
ax2 = p.plot(color='r', secondary_y=True, style='-o', linewidth=2, rot=30)
ax2.set_ylim((0, 1.05))
ax2.set_xlim(-1, 18)
plt.annotate(format(p[2], '0.4%'), xy=(2, p[2]), xytext=(2*0.9, p[2]*0.9), 
             arrowprops=dict(arrowstyle='->', connectionstyle='arc3, rad=.2'))    # 绘制文本与箭头

• 得到的帕累托图如下，可见用水停顿时间约 95% 都在 0.3 分钟以内，而 6~13 分钟的频率很低：
  

2.2 数据预处理

1. 数据规约

• 数据规约的目的是去掉无用的属性，如热水器编号、有无水流（可以以水流量反映）、节能模式等都可以去掉
• 代码如下：

data = data.drop(['热水器编号', '有无水流', '节能模式'], axis=1)

• 得到的数据为：
  

2. 数据变换

• 数据变换的目的是划分一次完整用水事件，即根据用水停顿时间来判断前后两次用水是否为同一用水事件。
• 数据变换的关键点在于用水停顿时间阈值的选取，书中的阈值寻优方法是按各阈值划分得到的事件个数，使用一个斜率指标来进行评估，该斜率指标为某一个阈值后面四个点的平均斜率。
• 根据斜率指标寻找阈值的流程如下：

Created with Raphaël 2.2.0 开始 存在斜率指标<1的阈值? 取最小阈值 结束 最小的斜率指标<5? 取斜率指标最小的阈值 取默认阈值 4 min yes no yes no

• 得到最优阈值后，使用最优阈值划分一次用水事件。
• 实现代码如下：

'''划分一次用水的阈值寻优'''
n = 4    # 使用以后 4 个点的平均斜率
threshold = pd.Timedelta(minutes=5)    # 专家阈值
use_water = data[data['水流量'] != 0]    # 剔除未用水数据
# 定义获取事件数函数
def event_num(ts):
    d = use_water['发生时间'].diff() > ts    # 差分与阈值比较
    return d.sum() + 1    # 直接返回事件数
dt = [pd.Timedelta(minutes=i) for i in np.arange(1, 9, 0.25)]
h = pd.DataFrame(dt, columns=['阈值'])    # 定义阈值列
h['事件数'] = h['阈值'].apply(event_num)    # 计算每个阈值对应的事件数
h['斜率'] = h['事件数'].diff() / 0.25    # 计算每两个相邻点对应的斜率
h['斜率指标'] = h['斜率'].abs().rolling(4).mean()    # 采用其后n个斜率的绝对值平均作为斜率指标
if (h['斜率指标'] < 1).any():    # 如果存在斜率指标小于1的阈值，则取其中最小的阈值
    ts = h['阈值'][h['斜率指标'] < 1].min()
else:    # 不存在斜率指标小于1的阈值，将最小斜率指标与专家斜率指标 5 比较
    ts = h['阈值'][h['斜率指标'].idxmin() -n]   # 因为滚动了n个，所以需要-n	
    if ts > threshold:
    	ts = threshold

'''使用最优阈值划分一次用水事件'''
d = use_water.loc[:, '发生时间'].diff() > ts
use_water.loc[:, '事件编号'] = d.cumsum() + 1    # 事件编号从 1 开始

3. 属性构造

• 属性构造部分书中只给出了构造说明，没有给出具体实现方法，以下属性构造实现为本文原创，如有谬误欢迎指正。
• 需要构造的属性分为 4 类指标，时长指标，频率指标，用水的量化指标以及用水的波动指标。
• 根据书中给出的构造说明，分析各属性的计算方法，可以知道所有的属性都可以从一次完整用水事件开始时间，每条用水数据持续时间， 每条停顿数据持续时间，完整用水事件结束时间这四个时间点数据集得到。其中每条用水数据和每条停顿数据的持续时间可以合并为每条数据的持续时间，再定义一个0-1 列表，用来表示是否为用水，1 为是，0 为否。
• 各属性计算公式如下：
  • 用水开始时间 = 起始数据时间 - 数据传输频率 / 2
  • 用水结束时间 = 结束数据时间 + 数据传输频率 / 2
  • 总用水时长 = 用水结束时间 - 用水开始时间
  • 用水时长 = SUM(每条用水数据持续时间)
  • 每次停顿时长 = SUM(该次停顿中每条停顿数据持续时间)
  • 总停顿时长 = SUM(每次停顿时长)
  • 平均停顿时长 = 总停顿时长 / 停顿次数
  • 停顿次数 = LEN(每次停顿时长)
  • 总用水量 = SUM(每条用水数据持续时间 × 每条用水数据水流量)
  • 平均水流量 = 总用水量 / 用水时长
  • 水流量波动 = SUM((每条用水数据水流量 - 平均水流量)^2 * 每条用水数据持续时间) / 用水时长
  • 停顿时长波动 = SUM((每次停顿时长 - 平均停顿时长)^2 * 每次停顿时长) / 总停顿时长
  • 是否为洗浴事件：同时满足总用水量>5L，用水时长>100s，总用水时长>120s的定义为洗浴事件
• 实现代码如下：

'''属性构造'''
# 将事件编号联合至原数据集
data2 = data.join(use_water[['事件编号']], how='outer')

# 获得热水事件对应的起始和终止编号
# 起始编号
start = data2[['事件编号']][data2['事件编号'].notnull()].drop_duplicates()    # 得到起始数据编号，保留重复值的第一个
start = start.reset_index()    # 重建索引，将数据编号变成列
start.columns = ['起始数据编号', '热水事件']
start = start.set_index('热水事件')
# 终止编号
end = data2[['事件编号']][data2['事件编号'].notnull()].drop_duplicates(keep='last')    # 得到终止数据编号，保留重复值的最后一个
end = end.reset_index()    # 重建索引，将数据编号变成列
end.columns = ['终止数据编号', '热水事件']
end = end.set_index('热水事件')

# 获得每个热水事件中，每条数据的开始时间、是否为用水
def get_time_and_use(x, start, end):
    time_axis = []    # 初始化每条数据时间点列表
    use = []    # 初始化是否为用水 0-1 列表
    datatime = data2['发生时间']
    diff = datatime.diff()
    usewater = data2['水流量']
    ds = pd.Timedelta(seconds=2)    # 设定传输时间频率为 2s
    for i in range(start.iloc[x, 0], end.iloc[x, 0] + 1):    # 遍历整个热水事件
        if i == start.iloc[x, 0]:    # 如果i为事件开始，以事件开始时间为该条用水开始时间，减去传输时间频率的一半
            time_axis.append(datatime[i] - ds / 2)
        else:       # 如果 i 不是事件开始，则该条用水开始时间为当前数据的时间减去与前一数据时间间隔的一半（两条数据中间时间点）
            time_axis.append(datatime[i] - diff[i] / 2)
        if usewater[i] == 0:    # 水流量为 0 则为停顿，否则为用水
            use.append(0)
        else:
            use.append(1)
    time_axis.append(datatime[i] + ds / 2)
    return pd.Series(time_axis), pd.Series(use)

# 计算各项属性
data3 = pd.DataFrame()
# 起始终止编号
data3 = pd.merge(start, stop, left_index=True, right_index=True)
# 初始化
start_times = []    # 用水开始时间
end_times = []    # 用水结束时间, 结束-开始为总用水时长
every_use = {}    # 每条用水数据持续时间，sum 为用水时长, 与每条的水流量相乘再求和为总用水量，总用水量/用水时长为平均水流量
stop_times = {}    # 每次停顿的时长，sum 为总停顿时长，len 为停顿次数，sum/len 为平均停顿时长
# 计算各次用水事件的各项数据
for j in range(len(start)):
    time_axis, use = get_time_and_use(j, start, end)
    # 计算用水起止时间：
    start_times.append(time_axis[0])
    end_times.append(time_axis[len(time_axis)-1])
    # 每条数据持续时间
    p = time_axis.diff()[1:]    # 差值的各项即为各条数据持续时间
    p.index = range(len(p))    # 重建索引
    # 每条用水数据持续时间
    every_use['{}'.format(j)] = list(p[use == 1].values / np.timedelta64(1, 's'))
    # 计算每次停顿的时长
    k = []    # 初始化
    for i in range(0, len(use) - 1):
        if (use[i] == 1) & (use[i + 1] == 0):    # 停顿开始
            stop_time = p[i + 1]
        elif (use[i] == 0) & (use[i + 1] == 0):    # 持续停顿，停顿时间持续增加
            stop_time += p[i + 1]
        elif (use[i] == 0) & (use[i + 1] == 1):    # 停顿结束，添加停顿时间
            k.append(stop_time)
    stop_times['{}'.format(j)] = k

# 构造各种属性
# 每次用水事件开始时间
data3['开始时间'] = start_times

# 每次用水事件总用水时长
data3['总用水时长'] = [(end_times[x] - start_times[x]) / np.timedelta64(1, 's') for x in range(len(start_times))]

# 每次用水事件总停顿时长、停顿次数、平均停顿时长
stop_all = []
stop_count = []
for x in range(len(stop_times)):
    if stop_times[str(x)]:
        stop_all.append(np.sum(stop_times[str(x)]) / np.timedelta64(1, 's'))
        stop_count.append(len(stop_times[str(x)]))
    else:
        stop_all.append(0)
        stop_count.append(0)
data3['总停顿时长'] = stop_all
data3['停顿次数'] = stop_count
data3['平均停顿时长'] = (data3['总停顿时长'] / data3['停顿次数']).fillna(0)

# 每次用水事件用水时长，用水时长比例
data3['用水时长'] = [np.sum(every_use[str(x)]) for x in range(len(every_use))]
data3['用水/总时长'] = data3['用水时长'] / data3['总用水时长']

# 每次用水事件总用水量、平均水流量
total_water = []
for i in range(len(every_use)):
    water = 0
    for j in range(len(every_use[str(i)])):
        water += use_water.iloc[i+j, 6] * every_use[str(i)][j]
    total_water.append(water / 60)
data3['总用水量'] = total_water
data3['平均水流量'] = data3['总用水量'] / data3['用水时长'] * 60

# 每次用水事件水流量波动
# 水流量波动 = sum((单条水流量 - 平均水流量)^2 * 单条持续时间) / 用水时长
water_vars = []
for i in range(len(every_use)):
    water_diff = 0
    for j in range(len(every_use[str(i)])):
        water_diff += (use_water.iloc[i+j, 6] - data3['平均水流量'][i+1]) ** 2 * every_use[str(i)][j]
    water_vars.append(water_diff / data3['用水时长'][i+1] /100)
data3['水流量波动'] = water_vars

# 每次用水事件停顿时长波动
# 停顿时长波动 = sum((单次停顿时长 - 平均停顿时长)^2 * 单次停顿时长) / 总停顿时长
stop_vars = []
for i in range(len(stop_times)):
    stop_diff = 0
    if len(stop_times[str(i)]) == 0:
        stop_vars.append(0)
    else:
        for j in range(len(stop_times[str(i)])):
            stop_time_i_j = stop_times[str(i)][j] / np.timedelta64(1, 's')
            stop_diff += (stop_time_i_j - data3['平均停顿时长'][i+1]) ** 2 * stop_time_i_j
        stop_vars.append(stop_diff / data3['总停顿时长'][i+1] / 10)
data3['停顿时长波动'] = stop_vars

# 用水时间点，即每天几点用水
data3['用水时间点'] = [x.hour for x in data3['开始时间']]

# 是否为洗浴（1为是，0为否）
data3['是否为洗浴'] = ((data3['总用水量'] > 5) & (data3['用水时长'] > 100) & (data3['总用水时长'] > 120)).astype(int)

• 得到的数据如下：
  

4. 数据清洗

• 书中对于缺失值进行了补全，不过个人认为意义不大，因为在划分用水事件的时候已经将停顿时间过长的数据筛选掉了，不存在一次用水事件中停顿时间过长的问题。对于用水时间，查看了用水时长的各项统计值（data3.describe()），未发现特殊值，而且即使存在用水时间过长，其中间时间段到底是真的用了这么久的水还是停顿了很久无法得知，不应该用补全的方法，而是应该剔除异常值。此处未发现异常值，因此未进行剔除。

2.3 模型构建

• 使用预处理后的数据集进行多层神经网络建模，使用前 80% 的数据作为训练集，后 20% 的数据为测试集。这里说明一点，由于上面的数据中是否为洗浴事件为推理出来的，并不一定准确，因此书中用的是用户自己记录的数据。
• 书中给出了最佳隐层节点数，这里并没有深究。模型的 batch_size 书中是 1，训练速度较慢，并且对于上面得到的数据集训练出来效果不佳，推测是因为数据集不同，修改 batch_size 为 1024，不仅速度大幅提升，而且训练效果非常好。
• 实现代码如下：

data_train = data3.iloc[:int(len(data) * 0.8), :]
data_test = data3.iloc[int(len(data) * 0.8):, :]
y_train = data_train.iloc[:, 15].values
x_train = data_train.iloc[:, 4:15].values
y_test = data_test.iloc[:, 15].values
x_test = data_test.iloc[:, 4:15].values

model = Sequential()
model.add(Dense(input_dim=11, units=17))
model.add(Activation('relu'))
model.add(Dense(input_dim=17, units=10))
model.add(Activation('relu'))
model.add(Dense(input_dim=10, units=1))
model.add(Activation('sigmoid'))
model.compile(loss='binary_crossentropy', optimizer='adam')
model.fit(x_train, y_train, epochs=100, batch_size=1024)

2.3 模型检验

• 使用书中给的混淆矩阵绘图模块进行可视化，训练集和测试集的结果分别如下：
• 训练集：
  
• 测试集：
  

3. 结语

数据分析挖掘过程中，数据预处理是最重要、难度最大、耗时最长的一部分，而书中对于这部分并没有详细说明，因此在参考书中属性构造公式的情况下，通过思考与实践，用相对简洁的方式，抓住数据的关键点，实现了十多个属性的构造。随后建立神经网络模型，调整神经网络参数，得到了不错的训练效果。