数据分析与挖掘:财政收入影响因素分析及预测模型
财政收入影响因素分析及预测模型
- 1. 背景与挖掘目标
- 2. 分析方法与过程
- 2.1 数据探索
- 2.2 模型构建
- 2.3 数据预测
1. 背景与挖掘目标
- 项目为《Python 数据分析与挖掘实战》第 13 章:财政收入影响因素分析及预测模型,内容参考了书中源代码及 u012063773 的博客
- 挖掘目标为分析地方财政收入的关键特征,筛选特征进行分析建模,然后对财政收入进行预测
2. 分析方法与过程
2.1 数据探索
- 主要变量描述性分析:可以看出 y 的波动很大
'''原始数据概括性度量'''
import numpy as np
import pandas as pd
inputfile = 'chapter13/demo/data/data1.csv'
data = pd.read_csv(inputfile)
r = [data.min(), data.max(), data.mean(), data.std()]
r = pd.DataFrame(r, index=['Min', 'Max', 'Mean', 'STD']).T
r = np.round(r, 2) # 保留两位小数
r
| Min | Max | Mean | STD | |
|---|---|---|---|---|
| x1 | 3831732.00 | 7599295.00 | 5579519.95 | 1262194.72 |
| x2 | 181.54 | 2110.78 | 765.04 | 595.70 |
| x3 | 448.19 | 6882.85 | 2370.83 | 1919.17 |
| x4 | 7571.00 | 42049.14 | 19644.69 | 10203.02 |
| x5 | 6212.70 | 33156.83 | 15870.95 | 8199.77 |
| x6 | 6370241.00 | 8323096.00 | 7350513.60 | 621341.85 |
| x7 | 525.71 | 4454.55 | 1712.24 | 1184.71 |
| x8 | 985.31 | 15420.14 | 5705.80 | 4478.40 |
| x9 | 60.62 | 228.46 | 129.49 | 50.51 |
| x10 | 65.66 | 852.56 | 340.22 | 251.58 |
| x11 | 97.50 | 120.00 | 103.31 | 5.51 |
| x12 | 1.03 | 1.91 | 1.42 | 0.25 |
| x13 | 5321.00 | 41972.00 | 17273.80 | 11109.19 |
| y | 64.87 | 2088.14 | 618.08 | 609.25 |
- 原始数据相关性分析:可以看出 x11 与 y 相关性不大,且为负相关
'''原始数据求解 Pearson 相关系数'''
pear = np.round(data.corr(method = 'pearson'), 2)
pear
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | x10 | x11 | x12 | x13 | y | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| x1 | 1.00 | 0.95 | 0.95 | 0.97 | 0.97 | 0.99 | 0.95 | 0.97 | 0.98 | 0.98 | -0.29 | 0.94 | 0.96 | 0.94 |
| x2 | 0.95 | 1.00 | 1.00 | 0.99 | 0.99 | 0.92 | 0.99 | 0.99 | 0.98 | 0.98 | -0.13 | 0.89 | 1.00 | 0.98 |
| x3 | 0.95 | 1.00 | 1.00 | 0.99 | 0.99 | 0.92 | 1.00 | 0.99 | 0.98 | 0.99 | -0.15 | 0.89 | 1.00 | 0.99 |
| x4 | 0.97 | 0.99 | 0.99 | 1.00 | 1.00 | 0.95 | 0.99 | 1.00 | 0.99 | 1.00 | -0.19 | 0.91 | 1.00 | 0.99 |
| x5 | 0.97 | 0.99 | 0.99 | 1.00 | 1.00 | 0.95 | 0.99 | 1.00 | 0.99 | 1.00 | -0.18 | 0.90 | 0.99 | 0.99 |
| x6 | 0.99 | 0.92 | 0.92 | 0.95 | 0.95 | 1.00 | 0.93 | 0.95 | 0.97 | 0.96 | -0.34 | 0.95 | 0.94 | 0.91 |
| x7 | 0.95 | 0.99 | 1.00 | 0.99 | 0.99 | 0.93 | 1.00 | 0.99 | 0.98 | 0.99 | -0.15 | 0.89 | 1.00 | 0.99 |
| x8 | 0.97 | 0.99 | 0.99 | 1.00 | 1.00 | 0.95 | 0.99 | 1.00 | 0.99 | 1.00 | -0.15 | 0.90 | 1.00 | 0.99 |
| x9 | 0.98 | 0.98 | 0.98 | 0.99 | 0.99 | 0.97 | 0.98 | 0.99 | 1.00 | 0.99 | -0.23 | 0.91 | 0.99 | 0.98 |
| x10 | 0.98 | 0.98 | 0.99 | 1.00 | 1.00 | 0.96 | 0.99 | 1.00 | 0.99 | 1.00 | -0.17 | 0.90 | 0.99 | 0.99 |
| x11 | -0.29 | -0.13 | -0.15 | -0.19 | -0.18 | -0.34 | -0.15 | -0.15 | -0.23 | -0.17 | 1.00 | -0.43 | -0.16 | -0.12 |
| x12 | 0.94 | 0.89 | 0.89 | 0.91 | 0.90 | 0.95 | 0.89 | 0.90 | 0.91 | 0.90 | -0.43 | 1.00 | 0.90 | 0.87 |
| x13 | 0.96 | 1.00 | 1.00 | 1.00 | 0.99 | 0.94 | 1.00 | 1.00 | 0.99 | 0.99 | -0.16 | 0.90 | 1.00 | 0.99 |
| y | 0.94 | 0.98 | 0.99 | 0.99 | 0.99 | 0.91 | 0.99 | 0.99 | 0.98 | 0.99 | -0.12 | 0.87 | 0.99 | 1.00 |
2.2 模型构建
1. Lasso 变量选择模型(备注:书中使用的是 Adaptive-Lasso 变量选择,这个函数多处查找都没找到,因此直接使用 Lasso,得到的结果和书中略有不同,后面保留的变量暂时以书中的为准)
'''Lasson 变量选择'''
from sklearn.linear_model import Lasso
model = Lasso(alpha=0.1, max_iter=100000)
model.fit(data.iloc[:, 0:13], data['y'])
print(model.coef_)
[-3.88351082e-04 -5.85234238e-01 4.38483025e-01 -1.25563758e-01
1.74517446e-01 8.19661325e-04 2.67660850e-01 2.89486267e-02
-7.55994563e+00 -8.62534215e-02 3.37878229e+00 0.00000000e+00
-7.70629587e-03]
2. 财政收入及各类别收入预测模型:各类别收入预测方法一样,因此以财政收入为例,描述灰色模型的计算过程,然后建立灰色预测与神经网络的组合预测模型,参数设置为误差精度10^-7,学习次数 10000 次,神经元个数为 6 个
-
灰色预测原理
灰色预测对原始数据进行生成处理如累加,生成有较强规律性的数据序列,然后建立相应的微分方程模型,从而预测事物未来发展趋势的状况。
设变量 X ( 0 ) = { X ( 0 ) ( i ) , i = 1 , 2 … n } X^{(0)} = \{X^{(0)}(i), i=1,2\dots n\} X(0)={X(0)(i),i=1,2…n} 为一非负单调原始数据数列,对 X ( 0 ) X^{(0)} X(0) 进行 1 次累加得到 X ( 1 ) = { X ( 1 ) ( k ) , k = 1 , 2 … n } X^{(1)} = \{X^{(1)}(k), k=1,2\dots n\} X(1)={X(1)(k),k=1,2…n},对 X ( 1 ) X^{(1)} X(1) 建立一阶线性微分方程,其中 a , u a, u a,u 为常数:
d X ( 1 ) d t + a X ( 1 ) = u \frac{dX^{(1)}}{dt} + aX^{(1)} = u dtdX(1)+aX(1)=u
求解微分方程,得到
X ( 1 ) ( t ) = [ ∫ e ∫ a ⋅ d x ⋅ u ⋅ d x + C ] ⋅ ∫ e ∫ − a ⋅ d x … … … … … … (1) X^{(1)}(t) = [\int e^{\int a\cdot dx} \cdot u \cdot dx+ C] \cdot \int e^{\int -a\cdot dx}\text {………………(1)} X(1)(t)=[∫e∫a⋅dx⋅u⋅dx+C]⋅∫e∫−a⋅dx………………(1)
⟹ X ( 1 ) ( t ) = ( u a ⋅ e a t + C ) ⋅ e − a t … … … … … … (2) \implies X^{(1)}(t) = (\frac {u}{a} \cdot e^{at} + C) \cdot e^{-at}\text {………………(2)} ⟹X(1)(t)=(au⋅eat+C)⋅e−at………………(2)
将 X ( 1 ) ( t 0 ) X^{(1)}(t_0) X(1)(t0) 代入(2),求解 C C C,得到:
C = ( X ( 1 ) ( t 0 ) − u a ) ⋅ e − a t 0 … … … … … … (3) C = (X^{(1)}(t_0) - \frac{u}{a}) \cdot e^{-at_0}\text {………………(3)} C=(X(1)(t0)−au)⋅e−at0………………(3)
将(3)代入(2),得到:
X ( 1 ) ( t ) = [ X ( 1 ) ( t 0 ) − u a ] ⋅ e − a ( t − t 0 ) + u a … … … … … … (4) X^{(1)}(t) = [X^{(1)}(t_0) - \frac{u}{a}]\cdot e^{-a(t-t_0)} + \frac{u}{a}\text {………………(4)} X(1)(t)=[X(1)(t0)−au]⋅e−a(t−t0)+au………………(4)
对于离散值:
X ( 1 ) ( k + 1 ) = [ X ( 1 ) ( 1 ) − u a ] ⋅ e − a k + u a … … … … … … (5) X^{(1)}(k+1) = [X^{(1)}(1) - \frac{u}{a}]\cdot e^{-ak} + \frac{u}{a}\text {………………(5)} X(1)(k+1)=[X(1)(1)−au]⋅e−ak+au………………(5)
灰色预测中对于 a , u a, u a,u 的求解使用的是最小二乘法。由于:
X ( 1 ) ( k ) − X ( 1 ) ( k − 1 ) = Δ X ( 1 ) ( k ) Δ k = X ( 0 ) ( k ) , Δ k = 1 … … … … … … (6) X^{(1)}(k) - X^{(1)}(k-1) = \frac{\Delta X^{(1)}(k)}{\Delta k} = X^{(0)}(k), \Delta k = 1\text {………………(6)} X(1)(k)−X(1)(k−1)=ΔkΔX(1)(k)=X(0)(k),Δk=1………………(6)
将(6) 代入微分方程,得到:
X ( 0 ) ( k ) = − a X ( 1 ) ( k ) + u … … … … … … (7) X^{(0)}(k) = -aX^{(1)}(k)+u \text {………………(7)} X(0)(k)=−aX(1)(k)+u………………(7)
由于 Δ X ( 1 ) ( k ) Δ k \frac{\Delta X^{(1)}(k)}{\Delta k} ΔkΔX(1)(k) 涉及 X ( 1 ) ( k ) X^{(1)}(k) X(1)(k) 两个时刻的值,因此将(7)中的 X ( 1 ) ( k ) X^{(1)}(k) X(1)(k) 换为两个时刻的均值更为合理,得到:
Y = B U Y = BU Y=BU
即:
[ X ( 0 ) ( 2 ) X ( 0 ) ( 3 ) ⋮ X ( 0 ) ( N ) ] = [ − 1 2 ( X ( 1 ) ( 2 ) + X ( 1 ) ( 1 ) ) 1 − 1 2 ( X ( 1 ) ( 3 ) + X ( 1 ) ( 2 ) ) 1 ⋮ ⋮ − 1 2 ( X ( 1 ) ( N ) + X ( 1 ) ( N − 1 ) ) 1 ] [ a u ] … … … … … … (8) \begin{bmatrix} X^{(0)}(2)\\ X^{(0)}(3)\\ \vdots\\ X^{(0)}(N)\\ \end{bmatrix} = \begin{bmatrix} -\frac{1}{2}(X^{(1)}(2) + X^{(1)}(1)) & 1 \\ -\frac{1}{2}(X^{(1)}(3) + X^{(1)}(2)) & 1 \\ \vdots & \vdots \\ -\frac{1}{2}(X^{(1)}(N) + X^{(1)}(N-1)) & 1 \\ \end{bmatrix} \begin{bmatrix} a \\ u \\ \end{bmatrix}\text {………………(8)} ⎣⎢⎢⎢⎡X(0)(2)X(0)(3)⋮X(0)(N)⎦⎥⎥⎥⎤=⎣⎢⎢⎢⎡−21(X(1)(2)+X(1)(1))−21(X(1)(3)+X(1)(2))⋮−21(X(1)(N)+X(1)(N−1))11⋮1⎦⎥⎥⎥⎤[au]………………(8)
由最小二乘法,得到:
U ^ = [ a ^ u ^ ] = ( B T B ) − 1 B T Y … … … … … … (9) \hat{U} = \begin{bmatrix} \hat{a} \\ \hat{u} \\ \end{bmatrix} = (B^TB)^{-1}B^TY\text {………………(9)} U^=[a^u^]=(BTB)−1BTY………………(9)
将(9)代入(5),得到:
X ( 1 ) ( k + 1 ) = [ X ( 1 ) ( 1 ) − u ^ a ^ ] ⋅ e − a ^ k + u ^ a ^ … … … … … … (10) X^{(1)}(k+1) = [X^{(1)}(1) - \frac{\hat{u}}{\hat{a}}]\cdot e^{-\hat{a}k} + \frac{\hat u}{\hat a}\text {………………(10)} X(1)(k+1)=[X(1)(1)−a^u^]⋅e−a^k+a^u^………………(10)
将(10)代入(6):
X ( 0 ) ( k + 1 ) = ( 1 − e a ^ ) [ X ( 0 ) ( 1 ) − u ^ a ^ ] e − a ^ k … … … … … … (11) X^{(0)}(k+1) = (1-e^{\hat{a}})[X^{(0)}(1) - \frac{\hat{u}}{\hat{a}}]e^{-\hat{a}k}\text {………………(11)} X(0)(k+1)=(1−ea^)[X(0)(1)−a^u^]e−a^k………………(11)
'''灰色预测函数'''
def GM11(x0): #自定义灰色预测函数
import numpy as np
x1 = x0.cumsum() # 生成累加序列
z1 = (x1[:len(x1)-1] + x1[1:])/2.0 # 生成紧邻均值(MEAN)序列,比直接使用累加序列好,共 n-1 个值
z1 = z1.reshape((len(z1),1))
B = np.append(-z1, np.ones_like(z1), axis = 1) # 生成 B 矩阵
Y = x0[1:].reshape((len(x0)-1, 1)) # Y 矩阵
[[a],[u]] = np.dot(np.dot(np.linalg.inv(np.dot(B.T, B)), B.T), Y) #计算参数
f = lambda k: (x0[0]-u/a)*np.exp(-a*(k-1))-(x0[0]-u/a)*np.exp(-a*(k-2)) #还原值
delta = np.abs(x0 - np.array([f(i) for i in range(1,len(x0)+1)])) # 计算残差
C = delta.std()/x0.std()
P = 1.0*(np.abs(delta - delta.mean()) < 0.6745*x0.std()).sum()/len(x0)
return f, a, u, x0[0], C, P #返回灰色预测函数、a、b、首项、方差比、小残差概率
'''地方财政收入灰色预测'''
import numpy as np
import pandas as pd
inputfile = 'chapter13/demo/data/data1.csv'
outputfile = 'chapter13/demo/tmp2/data1_GM11.xls'
modelfile = 'chapter13/demo/tmp2/net.model'
data = pd.read_csv(inputfile)
data.head()
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | x10 | x11 | x12 | x13 | y | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 3831732 | 181.54 | 448.19 | 7571.00 | 6212.70 | 6370241 | 525.71 | 985.31 | 60.62 | 65.66 | 120.0 | 1.029 | 5321 | 64.87 |
| 1 | 3913824 | 214.63 | 549.97 | 9038.16 | 7601.73 | 6467115 | 618.25 | 1259.20 | 73.46 | 95.46 | 113.5 | 1.051 | 6529 | 99.75 |
| 2 | 3928907 | 239.56 | 686.44 | 9905.31 | 8092.82 | 6560508 | 638.94 | 1468.06 | 81.16 | 81.16 | 108.2 | 1.064 | 7008 | 88.11 |
| 3 | 4282130 | 261.58 | 802.59 | 10444.60 | 8767.98 | 6664862 | 656.58 | 1678.12 | 85.72 | 91.70 | 102.2 | 1.092 | 7694 | 106.07 |
| 4 | 4453911 | 283.14 | 904.57 | 11255.70 | 9422.33 | 6741400 | 758.83 | 1893.52 | 88.88 | 114.61 | 97.7 | 1.200 | 8027 | 137.32 |
data.index = range(1994, 2014)
data.loc[2014] = None
data.loc[2015] = None
# 模型精度评价
l = ['x1', 'x2', 'x3', 'x4', 'x5', 'x7']
for i in l:
GM = GM11(data[i][list(range(1994, 2014))].values)
f = GM[0]
c = GM[-2]
p = GM[-1]
data[i][2014] = f(len(data)-1)
data[i][2015] = f(len(data))
data[i] = data[i].round(2)
if (c < 0.35) & (p > 0.95):
print('对于模型{},该模型精度为---好'.format(i))
elif (c < 0.5) & (p > 0.8):
print('对于模型{},该模型精度为---合格'.format(i))
elif (c < 0.65) & (p > 0.7):
print('对于模型{},该模型精度为---勉强合格'.format(i))
else:
print('对于模型{},该模型精度为---不合格'.format(i))
data[l+['y']].to_excel(outputfile, )
对于模型x1,该模型精度为---好
对于模型x2,该模型精度为---好
对于模型x3,该模型精度为---好
对于模型x4,该模型精度为---好
对于模型x5,该模型精度为---好
对于模型x7,该模型精度为---好
'''神经网络'''
inputfile2 = outputfile
outputfile2 = 'chapter13/demo/tmp2/revenue.xls'
modelfile = 'chapter13/demo/tmp2/1-net.model'
data2 = pd.read_excel(inputfile2, index_col=0)
# 提取数据
feature = list(data2.columns[:len(data2.columns)-1])
train = data2.loc[list(range(1994, 2014))].copy()
mean = train.mean()
std = train.std()
train = (train - mean) / std # 数据标准化,这里使用标准差标准化
x_train = train[feature].values
y_train = train['y'].values
# 建立神经网络模型
from keras.models import Sequential
from keras.layers.core import Dense, Activation
model = Sequential()
model.add(Dense(input_dim=6, units=12))
model.add(Activation('relu'))
model.add(Dense(input_dim=12, units=1))
model.compile(loss='mean_squared_error', optimizer='adam')
model.fit(x_train, y_train, epochs=10000, batch_size=16)
model.save_weights(modelfile2)
2.3 数据预测
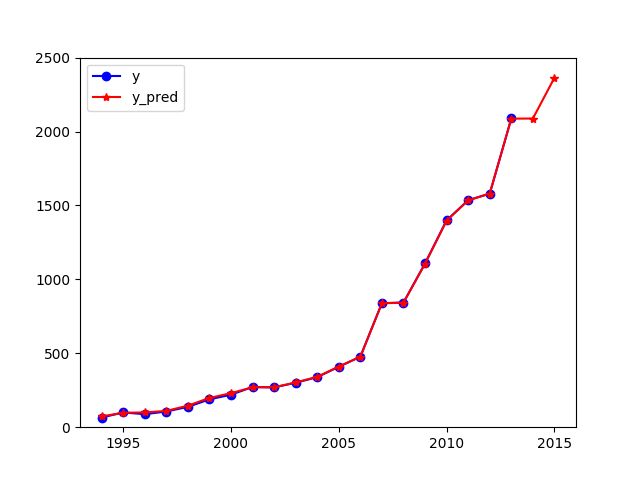
- 从结果可以看到,1994~2013 预测值和实际值几乎重合,因此数据预测可信度较高
# 预测,并还原结果
x = ((data2[feature] - mean[feature]) / std[feature]).values
data2['y_pred'] = model.predict(x) * std['y'] + mean['y']
data2.to_excel(outputfile2)
import matplotlib.pyplot as plt
%matplotlib notebook
p = data2[['y', 'y_pred']].plot(style=['b-o', 'r-*'])
p.set_ylim(0, 2500)
p.set_xlim(1993, 2016)
plt.show()
源代码及数据文件参考:https://github.com/Raymone23/Data-Mining