ML:利用 AdaBoost 元算法提高分类性能
利用 AdaBoost 元算法提高分类性能
- 1. 基于数据集多重抽样的分类器
- 1.1 bagging: 基于数据随机重抽样的分类器构建方法
- 1.2 boosting
- 2. 训练算法:基于错误提升分类器的性能
- 3. 基于单层决策树构建弱分类器
- 4. 完整 AdaBoost 算法的实现
- 5. 测试算法:基于 AdaBoost 的分类
- 6. 练习:在一个难数据集上应用 AdaBoost
- 7. 非均衡分类问题
- 7.1 正确率、召回率、ROC 曲线
- 元算法(meta-algorithm):对其他算法进行组合的一种方式
1. 基于数据集多重抽样的分类器
- 之前的文章中学习了五种不同的分类器:K 近邻,决策树,朴素贝叶斯,逻辑回归,支持向量机。它们各有优缺点,我们可以将不同的分类器组合起来,这种组合结果则称为集成方法(ensemble method)或者元算法。
- 集成方法有多种形式,可以是不同的算法的集成,也可以是同一算法在不同设置下的集成,还可以是数据集不同部分分配给不同分类器之后的集成。
1.1 bagging: 基于数据随机重抽样的分类器构建方法
- 自汇聚方法 (bootstrap aggregating),也称为 bagging 方法,是在从原始数据集选择 S 次后得到 S 个新数据集的一种技术。每个数据集都是原数据集有放回抽样得到的,大小和原数据集相等。
- 将某个学习算法分别作用于每个数据集就得到了 S 个分类器,对于新的数据集,应用这 S 个分类器进行分类,选择结果中最多的类别作为最终的分类结果
- 还有一些更先进的 bagging 方法,比如随机森林(Bagging + 决策树)
1.2 boosting
- boosting 与 bagging 类似,不过前者是通过串行训练得到的,每个分类器都根据已训练出的分类器的性能来进行训练。boosting 是通过集中关注被已有分类器错分的那些数据来获得新的分类器,即赋予这些数据更多的权重,并且每个弱分类器都有相应的权重,对于分类误差小的分类器会有更大的权重
- boosting 方法有多个版本,最流行的版本为 AdaBoost,其优点在于泛化错误率低,易编码,可以应用在大部分分类器上,无参数调整,缺点在于对离群点敏感
2. 训练算法:基于错误提升分类器的性能
AdaBoosting:Adaptive Boosting,自适应 Boosting,运行过程如下
- 训练数据中的每个样本,赋予一个权重,权重构成向量 D,初始时每个权重都相等
- 在训练数据上训练出一个弱分类器,计算该分类器的错误率,然后在同一数据集上再次训练弱分类器
- 在分类器的第二次训练中,将会重新调整每个样本的权重,其中第一次分对的样本的权重会降低,分错的样本的权重会提高
- 每个分类器都有一个权重值 alpha,该值是基于每个弱分类器的错误率进行计算的
- 错误率: ϵ = 未 分 类 正 确 的 样 本 数 目 所 有 样 本 数 目 \epsilon = \frac{未分类正确的样本数目}{所有样本数目} ϵ=所有样本数目未分类正确的样本数目
- alpha: α = 1 2 l n ( 1 − ϵ ϵ ) \alpha = \frac{1}{2}ln\left(\frac{1-\epsilon}{\epsilon}\right) α=21ln(ϵ1−ϵ)
- alpha 计算出来后,可以对D进行更新:
如果某个样本被正确分类: D i ( t + 1 ) = D i ( t ) e − α s u m ( D ) D_i^{(t+1)} = \frac{D_i^{(t)}e^{-\alpha}}{sum(D)} Di(t+1)=sum(D)Di(t)e−α如果某个样本被错误分类: D i ( t + 1 ) = D i ( t ) e α s u m ( D ) D_i^{(t+1)} = \frac{D_i^{(t)}e^{\alpha}}{sum(D)} Di(t+1)=sum(D)Di(t)eα
统一写作: D i ( t + 1 ) = D i ( t ) e − α ⋅ y i ⋅ y i ^ s u m ( D ) D_i^{(t+1)} = \frac{D_i^{(t)}e^{-\alpha\cdot y_i\cdot \hat{y_i}}}{sum(D)} Di(t+1)=sum(D)Di(t)e−α⋅yi⋅yi^ - 迭代计算 D,直到训练错误率为 0 或弱分类器数目达到指定值
3. 基于单层决策树构建弱分类器
- 单层决策树:决策树桩(decision stump),基于单个特征来做决策
- 对于下图中的数据,很明显该数据不能基于单个特征来分类,即选择一条平行于坐标轴的直线来分类。而通过多个单层决策树,可以构建出一个能够对该数据集完全正确分类的分类器
- 首先,第一个函数 stump_classify 即根据输入的判断标识,判断特征值大于或小于阈值,得到并返回分类结果
def stump_classify(data_matrix, dim, thresh_val, thresh_ineq):
'''
data_matrix: 输入矩阵
dim: 第几个特征
thresh_val: 阈值
thresh_ineq: 标识
'''
from numpy import *
retArray = ones((shape(data_matrix)[0],1))
if thresh_ineq == 'lt': # 标识为 lessthan 则小于阈值为 -1
retArray[data_matrix[:,dim] <= thresh_val] = -1.0
else: # 标识为 greaterthan 则小于阈值为 -1
retArray[data_matrix[:,dim] > thresh_val] = -1.0
return retArray
- 然后,第二个函数 build_stump 用于构建单层决策树,其输入为特征矩阵,分类标签,数据权重向量,输出最佳单层决策树,最小误差以及最佳分类结果。该函数遍历每个特征,每个特征值步长,每个不等号条件,总共三层循环,计算加权错误率,找到加权错误率最小的单层决策树。
def build_stump(data_arr, class_labels, D):
'''
Parameters:
data_arr: 特征数组
class_labels: 标签数组
D: 权重
returns:
best_stump: 最佳单层决策树
min_error: 最小误差
best_cls_est: 最佳的分类结果
'''
from numpy import *
data_mat = mat(data_arr)
label_mat = mat(class_labels).T
m, n = shape(data_mat)
steps = 10.0 # 用于计算步长
best_stump = {} # 初始化最佳单层决策树
best_cls_est = mat(zeros((m,1))) # 初始化最佳的分类结果
min_error = inf # 初始化最小误差为正无穷
for i in range(n): # 遍历每个特征
range_min = data_mat[:,i].min() # 特征最小值
range_max = data_mat[:,i].max() # 特征最大值
step_size = (range_max - range_min) / steps # 计算遍历步长
for j in range(-1, int(steps) + 1): # 遍历每个步长
for inequal in ['lt', 'gt']: # 遍历每种不等式
thresh_val = (range_min + float(j) * step_size) # 通过步长计算阈值
predicted_val = stump_classify(data_mat, i, thresh_val, inequal) # 预测值
err_arr = mat(ones((m, 1))) # 初始化误差矩阵
err_arr[predicted_val == label_mat] = 0
weighted_error = D.T * err_arr # 根据权重计算误差
print('split: idm %d, thresh %.2f, thresh inequal: %s, \
the weighted error is %.3f' % (i, thresh_val, inequal, weighted_error))
if weighted_error < min_error: # 找到误差最小的分类方式
min_error = weighted_error
best_cls_est = predicted_val.copy()
best_stump['dim'] = i
best_stump['thresh'] = thresh_val
best_stump['ineq'] = inequal
return best_stump, min_error, best_cls_est
- 载入数据,并测试结果:
def load_simp_data():
data = matrix([[1., 2.1],[1.5,1.6],[1.3,1.],[1.,1.],[2.,1.]])
labels = [1.0, 1.0, -1.0, -1.0, 1.0]
return data, labels
data, labels = load_simp_data()
D = mat(ones((5,1)) / 5)
build_stump(data, labels, D)
[Out]: ({'dim': 0, 'thresh': 1.3, 'ineq': 'lt'}, matrix([[0.2]]), array([[-1.],[ 1.],[-1.],[-1.],[ 1.]]))
- 上面构建的单层决策树即弱分类器,我们将使用多个若分类器来构建 AdaBoost 代码
4. 完整 AdaBoost 算法的实现
-
伪代码如下:
对每次迭代: 利用 build_stump 函数找到最佳的单层决策树 将最佳单层决策树加入到单层决策树组 计算 alpha 计算新的权重向量 D 更新累计类别估计值 如果错误率等于 0,则退出循环
'''基于单层决策树的 AdaBoost 训练过程'''
def ada_boost_train_ds(data_arr, class_labels, num_iter=40):
'''
Parameters:
data_arr: 输入矩阵
class_labels: 输入标签
num_iter: 最大迭代次数
Returns:
weak_class_arr: 弱分离器数组
'''
weak_class_arr = [] # 初始化单层决策树数组
m = shape(data_arr)[0] # 数据量大小
D = mat(ones((m,1)) / m) # 初始化数据权重向量
agg_class_est = mat(zeros((m,1))) # 初始化每条数据的类别估计累计值
for i in range(num_iter):
best_stump, error, class_est = build_stump(data_arr, class_labels, D)
print('D: ', D.T)
alpha = float(0.5 * log((1.0 - error) / max(error, 1e-16))) # 计算分类器权重,1e-16 避免除零错误
best_stump['alpha'] = alpha
weak_class_arr.append(best_stump)
print('class_est: ', class_est.T)
expon = multiply(-1 * alpha * mat(class_labels).T, class_est) # 计算指数项
D = multiply(D, exp(expon))
D = D / D.sum()
agg_class_est += alpha * class_est # 每条数据的类别估计累计值
print('agg_class_est: ', agg_class_est.T)
# 计算训练错误率
agg_errors = multiply(sign(agg_class_est) != mat(class_labels).T, ones((m,1)))
error_rate = agg_errors.sum() / m
print('total error: ', error_rate, '\n')
if error_rate == 0.0:
break
return weak_class_arr
classifier_array = ada_boost_train_ds(data, labels, 9)
[Out]:
D: [[0.2 0.2 0.2 0.2 0.2]] # 初始权重都相等
class_est: [[-1. 1. -1. -1. 1.]]
agg_class_est: [[-0.69314718 0.69314718 -0.69314718 -0.69314718 0.69314718]] # 第一个数据被错分
total error: 0.2
D: [[0.5 0.125 0.125 0.125 0.125]] # 第一条数据权重增加
class_est: [[ 1. 1. -1. -1. -1.]]
agg_class_est: [[ 0.27980789 1.66610226 -1.66610226 -1.66610226 -0.27980789]] # 最后一个数据被错分
total error: 0.2
D: [[0.28571429 0.07142857 0.07142857 0.07142857 0.5 ]] # 最后一个数据权重增加
class_est: [[1. 1. 1. 1. 1.]]
agg_class_est: [[ 1.17568763 2.56198199 -0.77022252 -0.77022252 0.61607184]] # 全部分类正确
total error: 0.0
classifier_array # 三个弱分类器及其权重
[Out]:
[{'dim': 0, 'thresh': 1.3, 'ineq': 'lt', 'alpha': 0.6931471805599453},
{'dim': 1, 'thresh': 1.0, 'ineq': 'lt', 'alpha': 0.9729550745276565},
{'dim': 0, 'thresh': 0.9, 'ineq': 'lt', 'alpha': 0.8958797346140273}]
5. 测试算法:基于 AdaBoost 的分类
- 一旦拥有了多个分类器及其对应的 alpha 值,我们就可以进行测试了,每个弱分类器的结果加权求和就是我们的最终结果
'''AdaBoost 分类函数'''
def ada_classify(data_to_class, classifier_array):
'''
Parameters:
data_to_class: 待分类数据
classifier_array: 弱分类器组成的数组
Returns:
sign(agg_class_est): 最终分类结果
'''
data_mat = mat(data_to_class)
m = shape(data_mat)[0]
agg_class_est = mat(zeros((m,1))) # 结果初始化
for i in range(len(classifier_array)):
class_est = stump_classify(data_mat, classifier_array[i]['dim'], classifier_array[i]['thresh'],
classifier_array[i]['ineq']) # 每个弱分类器的分类结果
agg_class_est += classifier_array[i]['alpha'] * class_est # 结果加权
print(agg_class_est)
return sign(agg_class_est)
ada_classify([[5, 5],[0, 0]], classifier_array)
[Out]:
[[ 0.69314718]
[-0.69314718]]
[[ 1.66610226]
[-1.66610226]]
[[ 2.56198199]
[-2.56198199]]
matrix([[ 1.],
[-1.]])
6. 练习:在一个难数据集上应用 AdaBoost
def load_data_set(filename):
num_feat = len(open(filename).readline().split('\t'))
data_mat = []
label_mat = []
fr = open(filename)
for line in fr.readlines():
line_arr = []
cur_line = line.strip().split('\t')
for i in range(num_feat - 1):
line_arr.append(float(cur_line[i]))
data_mat.append(line_arr)
label_mat.append(float(cur_line[-1]))
return data_mat, label_mat
data, labels = load_data_set('Ch07/horseColicTraining2.txt')
classifier_array = ada_boost_train_ds(data, labels, 10)
[Out]: ...total error: 0.23076923076923078
test_d, test_l = load_data_set('Ch07/horseColicTest2.txt')
predict = ada_classify(test_d, classifier_array)
err = mat(ones((67,1)))
err[predict != mat(test_l).T].sum() / 67
[Out]: 0.23880597014925373
- 通常情况下,测试错误率会达到一个稳定值,而不会随弱分类器的增加而降低。对于上述数据集,测试发现测试错误率在达到最小值后又开始升高,这称为过拟合。
7. 非均衡分类问题
- 前面的所有分类中,我们都假设所有类别的分类代价是一样的。但大多数情况下不同类别的分类代价并不相等,我们有一些其他分类性能度量指标,可以将代价考虑在内
7.1 正确率、召回率、ROC 曲线
- 混淆矩阵:预测值和实际值组成的矩阵
- 正确率:预测为正中真正为正的比例 P r e c i s i o n = T P T P + F P Precision = \frac{TP}{TP+FP} Precision=TP+FPTP
- 召回率:预测为正中真正为正的数据占所有真正为正的数据的比例 R e c a l l = T P T P + F N Recall = \frac{TP}{TP+FN} Recall=TP+FNTP
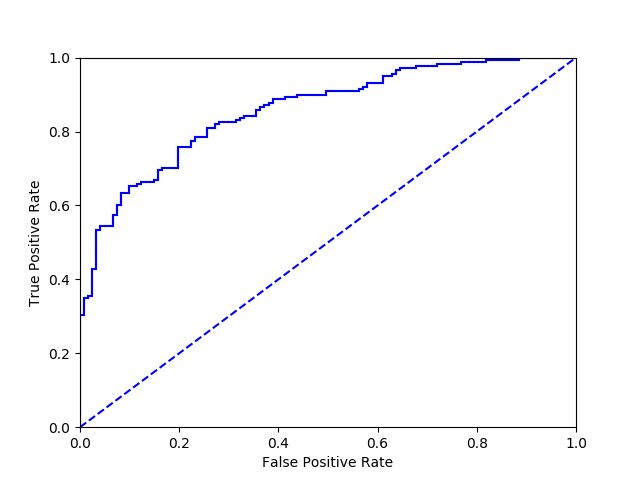
- ROC 曲线:横坐标为假阳率(FP / (FP+TN), 错分为正的数据占所有真正为负的比例),纵坐标为真阳率(召回率),原点为将所有样本判为负的情况,(1,1)为将所有样本判为正的情况。好的分类器 ROC 曲线应尽可能地处于左上角,即在低假阳率的情况下得到高的真阳率。
- 绘制 ROC 曲线的代码如下:
def plotROC(pred_str, labels):
'''
Parameters:
pred_str: 分类器的预测强度
labels: 实际标签
'''
import matplotlib.pyplot as plt
cur = (1.0,1.0) # 从 (1.0, 1.0) 开始绘制,即所有数据都判为正
y_sum = 0.0 # 计算曲线下面积
num_pos_cls = sum(array(labels) == 1.0) # 为正的数量
y_step = 1/ float(num_pos_cls) # y 轴步长
x_step = 1/ float(len(labels) - num_pos_cls) # x 轴步长
sorted_idx = pred_str.argsort() # 获取从小到达排序的索引值
fig = plt.figure()
fig.clf()
ax = plt.subplot(111)
for index in sorted_idx.tolist()[0]:
if labels[index] == 1.0: # 如果该样本为 1,则修改真阳率
del_x = 0
del_y = y_step
else: # 如果该样本不为 1,则修改假阳率
del_x = x_step
del_y = 0
y_sum += cur[1] # 高度累加方便计算面积
ax.plot([cur[0], cur[0]-del_x], [cur[1], cur[1]-del_y], c='b')
cur = (cur[0]-del_x, cur[1]-del_y)
ax.plot([0, 1], [0, 1], 'b--') # 绘制随机猜测曲线
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
ax.axis([0,1,0,1])
plt.show()
print('the area under the curve is: ', y_sum * x_step)