并查集（union-find）算法详解

之前很多连通性问题，其实都是可以通过并查集算法去实现的，比如城镇的修路问题：
首先在地图上给你若干个城镇，这些城镇都可以看作点，然后告诉你哪些对城镇之间是有道路直接相连的。最后要解决的是整幅图的连通性问题。比如随意给你两个点，让你判断它们是否连通，或者问你整幅图一共有几个连通分支，也就是被分成了几个互相独立的块。像畅通工程这题，问还需要修几条路，实质就是求有几个连通分支。如果是1个连通分支，说明整幅图上的点都连起来了，不用再修路了；如果是2个连通分支，则只要再修1条路，从两个分支中各选一个点，把它们连起来，那么所有的点都是连起来的了；如果是3个连通分支，则只要再修两条路…
读完《算法》第4版关于并查集的介绍后，觉得对这个算法有了比较完整的了解，这里简单记录一下。

动态连通性

这幅图是比较经典的动态连通性图，这个图会不断的接受整数对的输入，比如(p，q)，它代表p和q是相连的，这种相连具有自反性，对称性和传递性。他的动态体现在这个图随着输入的不断增加，连通性会发生变化。算法的目标就是，当输入(p，q)时，就使p和q连接起来。这里分为两种情况：
1.p和q本来就是连通的，那么放弃这个整数对
2.p和q不连通，则在p和q之间加一条路径
要实现上述目的，我们可以定义一个API，其中，连通分量表示该图的连通子图

---

UnionFind(int n) 构造函数，初始化N个触点
void union(int p, int q)  在p和q之间增加一条连接，若已连通，则不做更改
int find(int p) 返回p触点所在的连通分量的标识
boolean connected(int p, int q) 判断p和q是否存在于同一个连通分量中
int count() 连通分量的数量

---

代码的基本结构如下：

public class UnionFind {
    private int[] id;    //连通分量，用分量中的某个触点作为索引
    private int count;    //分量的数量
    private int[] size;     //每个分量的节点数量

    public UnionFind(int n){
        id = new int[n];
        count = n;
        for(int i = 0; i < n; i++) id[i] = i;
    }

    public int count(){
        return count;
    }

    public boolean connected(int p, int q){
        return quFind(p) == quFind(q);
    }

    public int find(int p)；//下面实现

    public void union(int p, int q)；//下面实现

    public static void main(String[] args){
    int[] left = {9, 3, 5, 7, 2, 5, 0, 4, 3};
        int[] right = {0, 4, 8, 2, 1, 7, 3, 2, 5};
        UnionFind unionFind = new UnionFind(100, true);
        for(int i = 0; i < left.length; i++){
            if(unionFind.connected(left[i], right[i])) continue;
            unionFind.jqUnion(left[i], right[i]);
            System.out.println("ID：");
            for(int j = 0; j < 10; j++) {
                System.out.print(unionFind.id[j] + " ");
            }
            System.out.println("size：");
            for(int j = 0; j < 10; j++) {
                System.out.print(unionFind.size[j] + " ");
            }
            System.out.println();
        }
    }

其中，find方法和union方法是这个方法的核心，所以并查集又叫做union-find算法。这两个方法的实现有三种方法，其中各有优劣。

quick-find 算法

顾名思义，这个方法是以最快find为目的的，这个算法可以在o(1)的复杂度判断两个触点是否相连，但是却只能以o(n)复杂度进行添加。这个算法的思想是保证在一个分量中所有的触点都有同样的标识，为了实现这一点，刚开始的时候，各个触点各自形成自己的分量，当有输入的时候，就将触点合并，union方法通过将p的标识符变为q（或者将q的标识符变成p）来实现合并，但是光改p一个点是不够的，还得把p所在分量的所有点都改成q的标识符，这就意味着需要遍历整个数组，来找到p所在分量的所有点，因此复杂度为o(n)，合并过程如下图，5和9合并，将5所在的分量1全部改为了9所在的分量8。

但是union的高昂代价给find方法带来了便利，因为find只需要访问数组p索引下的值，就可以知道它属于哪个分量了，判断两个点是否在同一个分量将会十分容易，复杂度仅o(1)。假设有m个点，他的union复杂度就为o(mn)，平方级的复杂度让他很难胜任大规模数据的union。代码如下：

    /*
    quick-find
     */
    public int qfFind(int p){
        return id[p];
    }

    public void qfUnion(int p, int q){
        int pId = qfFind(p);
        int qId = qfFind(q);
        if(qId == pId) return;
        for(int i = 0; i < id.length; i++){
            if(id[i] == pId)
                id[i] = qId;
        }
        count--;
    }

quick-union

quick-union采用了一种完全不同的思路，就是树。树结构有一个特点，就是移动一棵树不需要把整棵树的结点都移过去，只需要移动根节点就行了。在上面的分析中我们发现，quick-find算法的union复杂度之所以高，就是因为每次移动一个分量，需要把所有该分量的标识符都改变。改成树结构之后，我把一个分量的所有点用一颗树串联起来，当两个分量合并的时候，只需要把一棵树的根节点嫁接到另一颗树的根节点上即可。此时的id数组结构如下图

每个数组元素不再记录自己分量的标识，而是记录自己的父结点，根节点的父结点就是自己。所以，find函数的实现就是向上不断寻找找到任意结点的根节点，也就是id[index]=index的那个点，若两个点是连通的，他们必定有同一个根节点。union函数就是把p所在树的根节点连到q所在树的根节点上（反之也可以），实现树的合并。代码如下

    public int quFind(int p){
        while(id[p] != p) p = id[p];
        return p;
    }

    public void quUnion(int p, int q){
        int pId = quFind(p);
        int qId = quFind(q);
        if(qId == pId) return;
        id[pId] = qId;
        count--;
    }

quick-union方法看似让合并变的更加快速，其实不然，因为在合并之前，有两次find操作，而find操作的复杂度，是树的高度h，极端情况下，h=n，如下图。意味着union操作也会达到o(n)复杂度，随着树高度的增加，这个算法的复杂度会越来越高，面对大规模数据的时候仍显得吃力。

加权quick-union

这是几乎最优的解法了，前面分析了，quick-union算法不适合大规模数据的主要原因是因为树高的限制，那么只需要控制好树的高度，quick-union算法的复杂度就有很好的表现。控制的方法也很简单，就是总是让较小的树嫁接在较大树的根节点下。实现的方式也很简单，额外设一个size数组，记录每个分量的大小，也就是结点数。合并的时候，总是将size较小的树合并到size较大的树上去。可以证明，树的高度不会超过logN(2为底，高度从0开始），最坏的复杂度也不过是o(mlogn)，应付大规模的数据，已经足够了。

    public int jqFind(int p){
        while(id[p] != p) p = id[p];
        return p;
    }

    public void jqUnion(int p, int q){
        int pId = jqFind(p);
        int qId = jqFind(q);
        if(connected(p, q)) return;
        if(size[pId] < size[qId]){
            id[pId] = qId;
            size[qId] += size[pId];
        }else {
            id[qId] = pId;
            size[pId] += size[qId];
        }
        count--;
    }

和普通的quick-union比起来，树的高度是明显的

但是这个算法其实还有优化空间，理想情况下，树是可以做到高度为1的，也就是只有两层，这个时候，find和union的复杂度都将是o(1)，但这是不可能的。采用压缩路径的加权quick-union可以逼近这个复杂度，他的思想就是在find的时候，把经过的结点直接接到根节点上，这只需要增加一个while循环即可，就不再列举代码了。几种算法的对比如下

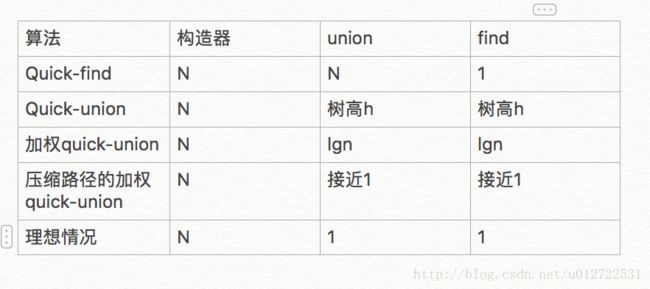
对大规模数据进行处理，使用平方阶的算法是不合适的，比如简单直观的Quick-Find算法，通过发现问题的更多特点，找到合适的数据结构，然后有针对性的进行改进，得到了Quick-Union算法及其多种改进算法，最终使得算法的复杂度降低到了近乎线性复杂度。

如果需要的功能不仅仅是检测两个节点是否连通，还需要在连通时得到具体的路径，那么就需要用到别的算法了，比如DFS或者BFS
参考文献：《算法》第四版.第一章.1.5节
http://blog.csdn.net/dm_vincent/article/details/7655764
http://blog.csdn.net/dellaserss/article/details/7724401/