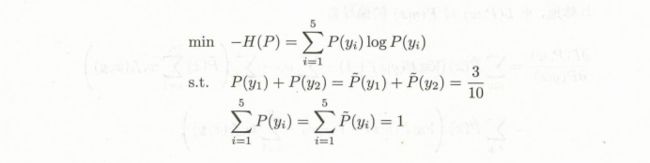July 3
梦入少年丛 歌舞匆匆 老僧夜半误鸣钟
惊起西窗眠不得 卷地西风
1. Logistic regression
Some basic logic
source: https://www.vebuso.com/2020/02/linear-to-logistic-regression-explained-step-by-step/
对我这种线代忘的一干二净的人还是要从头捋一捋
The basic idea behind logits is to use a logarithmic function to restrict the probability values between 0 and 1.
关于logit和probit,最大的区别就是一个是用log distribution,一个是normal distribution
Logistic assumptions
- The model is correctly specified.
- The cases are independent.
- The independent variables are not linear combinations of each other.
对于Logits:
If the probability of Success is P, then the odds of that event is: P / (1-P)
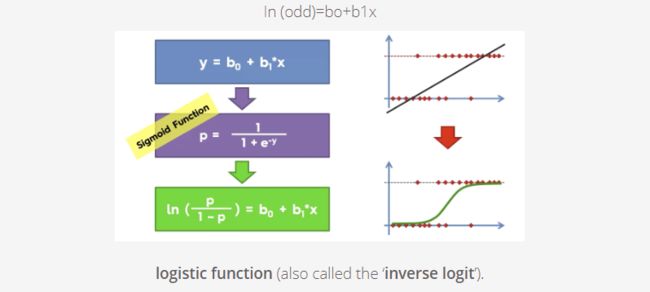
It’s time…. to transform the model from linear regression to logistic regression using the logistic function.
We can see from the below figure that the output of the linear regression is passed through a sigmoid function (logit function) that can map any real value between 0 and 1.
给一个logistic分布的定义:
线性函数的值越接近于正无穷,概率接近于1. 越接近负无穷,概率越接近0
多项逻辑:
Multinomial logistic regression is an expansion of logistic regression in which we set up one equation for each logit relative to the reference outcome
Multinomial logistic regression is used when you have a categorical dependent variable with two or more unordered levels (i.e. two or more discrete outcomes).
This type of regression is usually performed with software. Essentially, the software will run a series of individual binomial logistic regressions for M – 1 categories (one calculation for each category, minus the reference category).
2. 最大熵模型 maximum entropy model ((MaxEnt)
- 概率学习模型的一个准则 即熵最大的模型就是最好的模型
几何解释:
先回忆一下熵的概念:
The maximum entropy principle (MaxEnt) states that the most appropriate distribution to model a given set of data is the one with highest entropy among all those that satisfy the constrains of our prior knowledge.
也就是有着一堆期望
- 即为约束最优化问题
ok 那基于我浅薄的数学知识,我又要 回顾一下约束optimization是个什么登西 即 min f(x); s,t h(x) ≤ 0 【s,t 就是subject to的意思 哭泣了我真是数盲 谁能想到有一天我竟然在看这些】
也就是找一个东西满足这两个式子
也就是:
那就可以引入一个限制因子 λ 把这个问题转化为一个标准的拉格朗日dual problem 或者对偶问题来解决:
![]()
复杂点的写法也可以是:
然后我们就有:
让我们回到最大熵模型里来
已知
按照最优化的习惯,我们把最大化改为最小化问题:
用上辣个拉格朗日乘子定义函数 L (P,w)
举个例子
假设随机变量 X 有5个取值 {A,B,C,D,E}, 要估计各个值的概率 P(A), P(B), P(C), P(D), p(E).
那首先根据之前最大熵原理,在没有更多信息时,不确定的部分是等可能的。那么我们可以假设这些概率值满足:
P(A) + p(B) + p(C) + p(D) + p(E) = 1 P(A)= P(B)= P(C)= P(D)= p(E) = 1/5
为了学习这个例子中的最大熵模型 我们给一个约束条件,例如 P(A) + P(B) = 3/10, 即 P(A) = P(B) = 3/20
为了方便,分别以 y1,y2,y3,y4,y5 表示 A B C D E, 于是最大熵学习的最优化问题是:
引进拉格朗日乘子 w0, w1, 定义函数:
然后就是求解对偶问题外部的极大化问题:
3. 模型学习的最优化算法
归结为 以 似然函数为目标函数的最优化问题 通常通过迭代算法求解。
累了 脑子转不动了 我得去看其他的了