#2_经典控制理论梳理和有趣的想法

一、总体

经典控制理论中时域与频域分析差别

参考：知乎

介绍时域方法和频域方法的主要内容。

（1）应用对象
时域分析一般要求应用对象有精确的数学方程，通过方程直接求解每一时刻系统状态和输出的变化情况，包括瞬态响应和稳态响应。频域分析对系统数学方程精确性要求相对较低，对于LTI系统，当输入是正弦信号，输出也是正弦信号，频率不变，只是幅值和相位发生变化，所以可以依据这个特性分析系统在不同频率处的幅频特性和相频特性。

（2）稳定分析
时域中稳定性分析手段主要有二，一是前述的根轨迹方法，二是劳斯-赫尔维茨判据。频域稳定性分析方法就很丰富了，Bode图/Nichols图/Nyquist图/零极点配置等。

（3）性能参数
时域分析一般考察零极点位置，上升时间，峰值时间，调节时间，时间延迟，阻尼比等等。频域分析主要考察复平面上幅相曲线对（-1，0j)点的穿越情况，也就是增益裕度/相位裕度，此外还有闭环带宽/穿越频率/共振频率等等性能参数。

（4）设计综合时域
综合方法有：针对一阶二阶系统的公式，基于系统型别的稳态误差调节，PID控制，根轨迹和劳斯-赫尔维茨判据法选取合适开环增益等等。在现代控制理论中，时域综合方法得到很大扩充，包括了状态反馈/输出反馈/极点配置/观测器/解耦控制/最优控制等等方法。

频域综合方法有：调节器如超前，滞后，超前滞后，bode图，Nichols图等。在现代控制理论中还有多项式矩阵综合方法。

二、时域

根轨迹法控制器设计

参考：知乎

熟悉根轨迹方法的会知道，零极点的配置问题大致过程为：
（1）将控制要求（Requirements）转化为s平面主导极点的位置；
（2）配置零极点使得根轨迹刚好通过那一点。

嗯，具体还需要查资料研究。

三、频域

Bode图稳定性判据的理解

参考：知乎

介绍如何从相位角度理解稳定性

判断环路稳定的第一步是把闭环打开，基于开环来分析，分析环路从输入到反馈这一条路径的时延（频域是相位延时）。如果开环的相位延时达到了180度，那么再加上负反馈本身的减号（再＋180度），这样参考源就和反馈是叠加了，结果是越来越不稳定（正反馈）。

对于Bode图，我们分析-180度位置的幅值情况，如果小于0db，也就是幅值小于1，就说明正反馈的成分是逐渐衰减的，那么系统就是稳定的。

Bode图稳定裕度的理解

参考：知乎

介绍如何稳定裕度的内涵以及问题

稳定裕度：margin。裕度margin是系统稳定性的表征，裕度越小，系统越不稳定，从而对误差鲁棒性更差。注意，稳定裕度始终是针对开环系统而言的。

不稳定系统会发散，可以认为稳定裕度无穷大。那么对于单位负反馈系统，闭环传递函数为：
$\frac{G(s)}{1+G(s)}$
不稳定系统可以认为分母为0，也就是$G(s)=-1$。这样我们得到了$(-1,0j)$这个点，这个点在Nyquist图中具有重要作用。开环传函$G(s)=-1$的Bode图为：

我们希望开环传函Bode图远离这两条红线。通过根轨迹、上面一小节的相位角度分析以及本节的分析，都能加深对稳定性判据的认识。

幅频裕度GM定义为-180°相位时，幅值负于0dB的量值，GM的含义是开环系统前面缩放项K的可变量，是针对系统所有通道而言的；相频裕度PM定义为幅值为0dB时，相位超前-180°的量值。按照这一小节的理解，就是尽可能远离图中的两条红线(从哪个方向远离暂时没有好的理解，可以由上一小节以及根轨迹角度补充理解)。

一般，放大增益(幅频曲线整体抬升，形状不变)和加入延迟环节(只延迟相位)，都会使得GM和PM同时降低。

Matlab中可以使用bode()、margin()函数分析。

稳定裕度有一定误导性，实际系统的稳定性信息并不能简单地通过GM和PM反映，实际上幅值裕度和相位裕度都是从整体上表征系统增益和相位延迟对稳定性的影响，不能表示某些单独变化会对系统稳定性造成什么影响，而后者就涉及到系统鲁棒性和参数敏感性的问题。

下面举两个例子说明：
例一：系统结构参数不准确
$G(s)=\frac{1.3(s+2)}{s^3+s^2+6s+1}$和$G(s)=\frac{1.3(s+2)}{s^3+s^2+3s+1}$虽然参数变化很小，但是稳定裕度差别很大：


例二：稳定裕度的不全面性
对于系统$G(s)=\frac{0.38\ast (s^2+0.1\ast s+0.55)}{(s\ast (s+1)\ast (s^2+0.06\ast s+0.5))}$，其Bode图和Nyquist图如下。可见虽然幅值裕度为无穷大，但是有一个相位上的尖峰，该点容易受到扰动突破$-180°$，使系统不稳定。从Nyquist图中可以清楚地看到靠近$(-1,j0)$的两个尖峰。

Bode图控制器设计

参考：知乎

主要介绍超前补偿、滞后补偿和综合运用。

基于Bode图的控制器之总体设计思路与根轨迹法类似：
（1）将控制要求（Requirements）转化为频域要求，如增益裕度（gain margin）、相位裕度（phase margin）、穿越频率（截止频率）、带宽、零频率幅值等等；
（2）依据估计公式设计超前滞后调节器的零极点。

超前/滞后控制器的结构如图：

当，${\omega }_z>{\omega }_p$，分子相位小于分母，因此使滞后的；反之，是超前的。此外，我们还需要补充放大系数和积分环节，用来保证稳态精度，因此一般形式为：

$Controller(s)=K\times \frac{1}{s^n}\times \frac{s+{\omega }_z}{s+{\omega }_p}$。

举例：对于系统$G(s)=\frac{1}{0.2s+1}$，我们要求对于斜坡信号稳态误差小于0.02，相位裕度大于48°，那么可以基于Bode图设计超前和滞后控制器，大致过程为：
（1）利用终值定理分析系统稳态误差，看是否满足要求，如果不满足则补充积分环节提高系统型别，注意积分环节越少越容易实现。本例我们增加一个积分环节（不增加则系统发散），此时稳态误差为非零常数，那么为了让稳态误差达到要求，再增加放大增益$K$，简单分析知取$K=50$即可。

（2）绘制$G(s)$的Bode图(加上刚刚设计的积分环节和增益系数)，分析系统的稳定性，并得到稳定裕度，看是否满足要求，不满足则通过增加超前/滞后/超前滞后控制器使系统满足要求。针对本例分别设计超前和滞后补偿器（设计过程后面再介绍），添加后的Bode图和阶跃响应为：

根据以上结果知：超前调节和滞后调节都能增大系统阻尼，减小超调，但还是有很大区别：超前校正的主要作用是提供一个超前相角，从而增大相位裕度，工程上主要用于改善系统的快速性和稳定性；滞后校正主要目的是适当衰减幅值增益，工程上主要用于提高系统稳态精度和稳定性，抑制高频噪声，但是降低了系统快速性。超前校正和滞后校正各有优点，且通过伯德图可以观察出其各自频率作用范围相互影响可以很小，因此可以共同使用，称为超前-滞后调节。

超前补偿

这个调节器将相位曲线在某一个频率段向上提升，而尽量不改变幅值曲线，这样就可以增加系统相位裕度。

考虑已经设计完毕比例和积分部分，只剩余超前部分。

超前调节从理论上来说最多可以增加90°的相位，但是实际上最多只能增加55°相位裕量。因此如果你需要增加超过55°的相位裕量，可以考虑使用两个超前调节器串联，这样从理论上说最多可以增加110°的相位裕量。

取如下形式：

这个形式零频率增益为0dB，不影响稳态误差，它的最大相位是：

此时的频率为：

最大相位处增益：

设计过程为：
（1）计算当前相位裕度和目标裕度的差值，并适当扩大差值。这样得到了需要超前的相位，我们用补偿器的最大相位处提高相位裕度，那么根据补偿器最大相位公式，可计算出$a_1$。
（2）根据公式计算补偿器此时增益$\sqrt{a_1}$，我们需要想办法抵消掉补偿器的幅值抬升，因此去原Bode图幅值曲线上找到$-\sqrt{a_1}$的位置，如果在此处让补偿器达到最大相位${\omega }_m$，那么此处恰好成为穿越频率处。我们把补偿器最大相位处的频率定在此处，那么可以计算出$\tau$。
（3）校验设计，不满足指标则对上述过程进行修正。

上述第二步骤也可以不那么麻烦，我们直接根据经验选择一个${\omega }_m$，反复校验即可。

滞后补偿

这个调节器主要目的是降低幅值，从而减小穿越频率，提高相位裕度。

类似地，设计如下形式：

同样可以得到最大相位、最大相位频率、最大相位幅值的公式。设计过程和超前补偿也是类似的。

我们希望伴随幅值下降的相位下降区域离截止频率点越远越好，这样就不会影响最终的相位裕度，这就要求把零极点尽可能的配置到离虚轴更近的点，即参数$\tau$一般越大越好，一个工程实际原则是将零点配置到离虚轴距离比主导极点近50倍的点。

超前-滞后调节

为了简化设计，可以采用如下的形式：

开环Bode图对系统性能的反应

参考：知乎

首先明确一下开环传递函数的概念，即图中的绿线$KG(s)H(s)$，注意是包括传感器传递函数的。从开环传递函数中，我们能明确知道系统由哪些环节构成，便于我们设计分析。

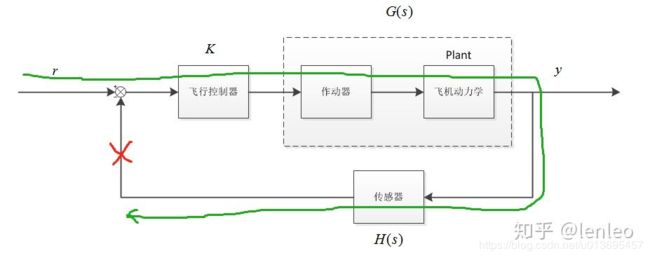
开环Bode图能够提供的信息：
[1].开环频率响应，进而可以通过图解法求得闭环频率响应（向量图/等M圆图/等N圆图）。
[2].稳定性特性——幅值裕度、相位裕度。
[3].开环伯德图的形状也表征了闭环系统的响应特性。

第一点其实直接用matlab画图就行了，第二点已经讨论很多了，这里强调下第三点：

我们可以把开环Bode分为三段，低频段反映了稳态特性，幅值越大越平稳则信号跟踪能力越强（显然穿越频率大一些，能提高低频幅值）；中频段反映了系统的稳定性，由于幅频曲线和相频曲线的关系近似于如下关系：在幅频斜率远离转折点的稳定区域，$\angle G(j\omega )\approx n\ast 90°$，其中n表示对数轴上的斜率(不转换为分贝)，可以参考这里，那么如果我们希望中频段的相位裕度是90°左右，就希望中频段幅值斜率为$-20dB/dec$；高频段则希望快速下降，从而抑制高频噪声。

闭环Bode图对系统性能的反应

用典型二阶系统举例：

其闭环Bode图主要提供幅值峰值$M_p$、峰值频率${\omega }_p$、带宽${\omega }_{BW}$三个信息，如下图：

对二阶系统经过分析有：
$M_p=\frac{1}{2\zeta \sqrt{1-{\zeta }^2}}$
${\omega }_p={\omega }_n\sqrt{1-2{\zeta }^2}$

绘制曲线分析可知：超调越大，幅值峰值越大

关于带宽的作用我们用二阶振荡系统举例：

可以得到带宽与调节时间、峰值时间、上升时间的关系：

四、实践

《控制系统设计指南》

双极点低通滤波器（无零点二阶环节）设计：
①作者建议使用阻尼比为0.4-0.6的双极点滤波器，虽然通带内不平坦，有一些超调，但是延迟较小。而具体的阻尼比可以依据系统的要求调试。
②闭环伯德图的凸峰也是衡量控制系统性能的一个指标，如果凸峰的值大于0，那系统则会有超调，本书作者建议，闭环伯德图的凸峰不应大于4dB。

《控制理论》 – 知乎专栏

这个专栏比较系统地整理了自控原理一书的知识点，需要的时候查看即可。

传递函数要求零初始条件的两个含义：