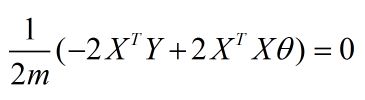对比梯度下降和正规方程解性能

现在用导数的方式模拟线性回归中的梯度下降法

首先再来回顾一下梯度下降法的基础

• 梯度下降法不是一个机器学习算法, 而是一个搜索算法
• 梯度下降法用在监督学习中
• 梯度下降法的过程: 对比模型输出值和样本值的差异不断调整本省权重, 直到最后模型输出值和样本标签差别达到理想误差范围内
• 梯度下降法的超参是梯度, 梯度过大会导致跳过最优或局部最优解, 梯度过小会过于消耗计算资源

现在写一个sklearn中的正规方程的线性回归模型 没有实现fit方法

import numpy as np
from .metrics import r2_score

class LinearRegression:

    def __init__(self):
        """初始化Linear Regression模型"""
        self.coef_ = None
        self.intercept_ = None
        self._theta = None

    def predict(self, X_predict):
        """给定待预测数据集X_predict，返回表示X_predict的结果向量"""
        assert self.intercept_ is not None and self.coef_ is not None, \
            "must fit before predict!"
        assert X_predict.shape[1] == len(self.coef_), \
            "the feature number of X_predict must be equal to X_train"

        X_b = np.hstack([np.ones((len(X_predict), 1)), X_predict])
        return X_b.dot(self._theta)

    def score(self, X_test, y_test):
        """根据测试数据集 X_test 和 y_test 确定当前模型的准确度"""

        y_predict = self.predict(X_test)
        return r2_score(y_test, y_predict)

    def __repr__(self):
        return "LinearRegression()"

因为这里是用线性回归做测试, 线性回归的正规方程解如下

此公式网上搜的, 推导过程可以看下这位老兄的博客 https://blog.csdn.net/chenlin41204050/article/details/78220280 (未经允许直接引用了哈)

实现正规方程解的fit如下:

    def fit_normal(self, X_train, y_train):
        """根据训练数据集X_train, y_train训练Linear Regression模型"""
        assert X_train.shape[0] == y_train.shape[0], \
            "the size of X_train must be equal to the size of y_train"
        X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
        self._theta = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y_train)
        self.intercept_ = self._theta[0]
        self.coef_ = self._theta[1:]
        return self

要用梯度下降法, 就得找到损失函数, 然后计算梯度
下面是多元线性回归的瞬时函数

线性回归的lose
接着实现上图面试的梯度下降法的fit_gd如下

    def fit_gd(self, X_train, y_train, eta=0.01, n_iters=1e4):
        """根据训练数据集X_train, y_train, 使用梯度下降法训练Linear Regression模型"""
        assert X_train.shape[0] == y_train.shape[0], \
            "the size of X_train must be equal to the size of y_train"
        def J(theta, X_b, y):
            try:
                return np.sum((y - X_b.dot(theta)) ** 2) / len(y)
            except:
                return float('inf')
            
        def dJ(theta, X_b, y):
            return X_b.T.dot(X_b.dot(theta) - y) * 2. / len(y)
            
        def gradient_descent(X_b, y, initial_theta, eta, n_iters=1e4, epsilon=1e-8):
            theta = initial_theta
            cur_iter = 0
            while cur_iter < n_iters:
                gradient = dJ(theta, X_b, y)
                last_theta = theta
                theta = theta - eta * gradient
                if (abs(J(theta, X_b, y) - J(last_theta, X_b, y)) < epsilon):
                    break
                cur_iter += 1
            return theta
            
        X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
        initial_theta = np.zeros(X_b.shape[1])
        self._theta = gradient_descent(X_b, y_train, initial_theta, eta, n_iters)
        self.intercept_ = self._theta[0]
        self.coef_ = self._theta[1:]
        return self

上面的方法都封装在一个LinearRegression.py中

现在开始测试
准备一些随机数据, 维度为5000, 样本数量1000

m = 1000
n = 5000

big_X = np.random.normal(size=(m,n))
true_theta = np.random.uniform(0.0, 100.0, size=n+1)
big_y = big_X.dot(true_theta[1:]) + true_theta[0] + np.random.normal(0, 10.0, size=m)
print(big_X.shape, big_y.shape)

%run LinearRegression.py

输出:

(1000, 5000) (1000,)

使用正规方程解训练线性回归

big_reg1 = LinearRegression()
%time big_reg1.fit_normal(X_train, y_train)
big_reg1.score(X_test, y_test)

输出:

CPU times: user 26.8 s, sys: 921 ms, total: 27.7 s
Wall time: 11.1 s
LinearRegression()

使用梯度下降法训练

big_reg2 = LinearRegression()
%time big_reg2.fit_gd(big_X, big_y)

输出:

CPU times: user 7.44 s, sys: 97.2 ms, total: 7.54 s
Wall time: 4.15 s
LinearRegression()

结论

• 梯度下降法在无法求出直接最优解的情况下 , 可以搜索到相对较优的解
• 梯度下降法在数据量较大的情况下, 可以避免类似于正规方程解因为数据规模变大带来的长时间运算(也是相对性的)