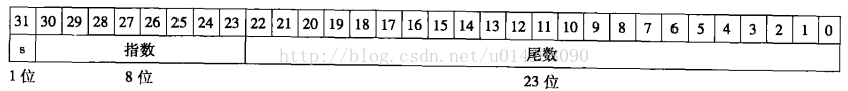单精度浮点数乘法的实现
按:计算机组成课程第四周作业
算法证明
图表 1 浮点数的表示
浮点数的表示如上图所示,我们要做的是将按如上方式存储的两个浮点数相乘,将其结果用如上的方式表示。
符号位只是两者的异或,指数位基本上是两指数的相加,而尾数位就需要在正常的乘法之余考虑到移位(和随之而来的指数为的溢出)和进位的情况。
下面就来讨论一下尾数的运算:
在尾数前补上1,进行无符号数乘法。小数点仅作为算法分析时的记号,实际上不参加运算。用64位的long long类型的数来存储运算结果。
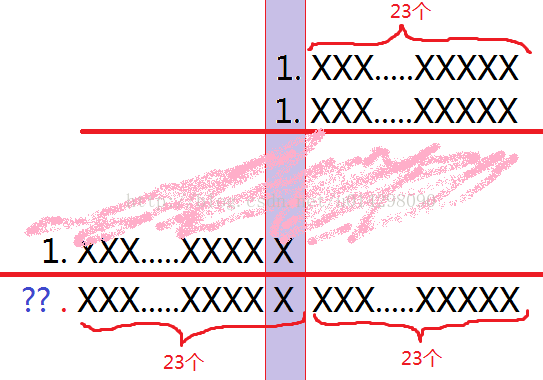
图表 2 尾数相乘(用“画图”程序画的)
如上图所示,后46个数字是结果的小数点后的数据,小数点的的问号处可能只有1,可能是1X(10或11,在算法中没有太大区别)。若问号处只有1,说明已经规格化完成;若是1X,需要将整个数右移一位,质数加一,从而使问号处只有1。
规格化后要进行round操作,如下图所示。如果第23位是0,这一位之前的23位就是所需要的尾数。如果第23位是1,截取这位之前的数,加一(类似于四舍五入)。判断结果是否仍规格化。若没有规格化,从规格化开始继续做,直到找到规格化后的23位尾数。
图表 3 有效数处理(用“画图”程序画的)
程序框图
主要流程如下图所示。在代码注释中的Step1到step5即分别对应流程图中的1至5部分。有所不同的是,因为后面只会增加exponent而不会减少,所以我的程序在step1就判断是否overflow,在step3也判断是否overflow就行了,规格化完成后再判断underflow。
图表 4 浮点乘法程序框图
使用方法
输入两个数,程序用自带的scanf将其作为单精度浮点数读入。通过一系列的无符号数的计算,得到用单精度浮点数表示的结果,将其输出(为了更详细地看到整个数,输出的数小数点后有20位)。如果overflow或underflow,输出的是相应的提示。为了验证计算是否正确,在输出的数据后面有个括号,里面放了是直接让机器进行的单精度浮点数的乘法的结果。
特殊处理
特殊输入数据
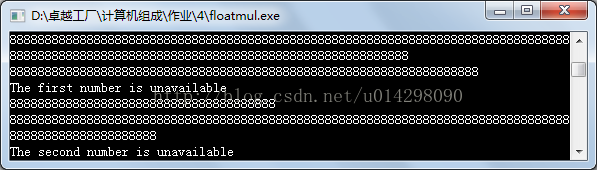
有些输入的数据是在太大或太小,以至于数据本身就已经overflow或underflow,从而根本无法存贮到单精度浮点数中,不是合法的单精度浮点数。对于这样的数,我们不应该对其提供任何服务,不然只会闹出笑话。
对于零要特殊处理,因为0在浮点数中的表示并不是按照一般的规范来的。
溢出
这里的溢出指的是乘数和被乘数本身是合法的单精度浮点数,但相乘后造成了溢出。
因为后面只会增加exponent而不会减少,所以与上面的流程图不同,我的程序在step1就判断是否overflow,在step3也判断是否overflow就行了,规格化完成后再判断underflow。
数位扩展
整个程序都是按照单精度的浮点数来写的,数位扩展可能有点麻烦。如果要扩展为双精度的,需要更改代码中的大量参数。鉴于浮点数一般也就只有单精度和双精度两种,我觉得不是太必要提高做成可扩展的。
实例分析
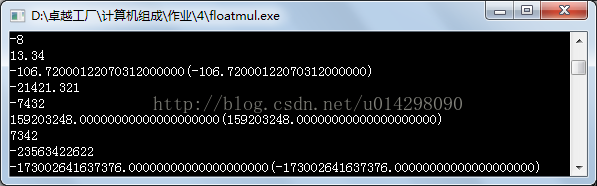
图表 5 大数的乘法
图表 6 overflow
图表 7 underflow(本程序判为underflow,而C语言自己的浮点数乘法计算结果为0.000000)
图表 8 对0的乘法
图表 9 很大的与很小的正数相乘
图表 10 观察精确度
图表 11 对负数乘法的测试
图表 12 对于无法用浮点数表示的输入数据
图表 13 对于过小的数据
结果分析
我们对过于大的数据和过于小的数据,以及精度太大的数据都做了试验。从上述结果可以看到,这个程序的结果与C程序自带的浮点数乘法结果基本吻合。说明这个程序还是比较可靠的。
通过对精度的测试,我们发现浮点数虽然能表示较大较小的数据,但有效数字还是有限的。如-100与0.6相乘的结果,整数部分60是对的,小数点五位后就出现了偏差。一连串8与1相乘,结果的头部只有7个8。可以大致地认为浮点数的表示与计算的十进制有效数位是7位。
可以更进一步的工作
l 程序中对于无符号整数的加法、乘法,对于exponent的有符号整数运算都是直接使用的,其实可以调用之前写的相关程序,做成更加本质的浮点数乘法。
Source Code
#include
union unionfloat{
float f;
unsigned long l;
};
union unionfloat x,y,product;
/*
disp(union unionfloat x)
{
long i;
unsigned long m;
printf("%f:",x.f);
m=0x80000000;
for(i=0; i<32; i++){
if((i&7)==0)printf(" ");
if(m&x.l)printf("1");
else printf("0");
m>>=1;
}
printf("\n");
}*/
int mul(void){
//Step 1
int exponent;
exponent=(x.l&0x7F800000)>>23;
exponent-=0x7F;
exponent+=(y.l&0x7F800000)>>23;
exponent-=0x7F;
if(exponent>=128) return 1;
//Step 2
unsigned long long raw_product;
unsigned long long raw_x=x.l&0x007FFFFF|0x00800000;
unsigned long long raw_y=y.l&0x007FFFFF|0x00800000;
int carry;
raw_product = raw_x * raw_y;
/* int i=64;
unsigned long long p=0x8000000000000000;
while(i--){
if(i%4==3)printf(" ");
if(raw_product&p)printf("1");
else printf("0");
p=p>>1;
}
printf("\n");*/
//相乘结果若小数点前有两位
do{
//Step 3
if(raw_product>>47){
raw_product = raw_product>>1;
exponent++;
if(exponent>=128) return 1;//printf("Overflow");
}
//Step 4
if(raw_product & 0x0000000000400000){
raw_product = ((raw_product>>23)+1)<<23;
}
}while(raw_product>>47);//still normalized?
//Step 5
product.l = ((x.l>>31)^(y.l>>31))<<31;
if(exponent<=-127) return -1;//printf("Underflow");
//-127>23));
//disp(product);
printf("%.20f(%.20f)\n",product.f,x.f*y.f);
return 0;
}
int main(void){
while(~scanf("%f%f",&x.f,&y.f)){
//printf("Input %.10f %.10f\n",x.f,y.f);
//disp(x);disp(y);
if(x.l==0||y.l==0)
printf("%f(%f)\n",0,x.f*y.f);
else if((((x.l>>23)&0x000000FF)==0) || (((x.l>>23)&0x000000FF)==0x000000FF))
printf("The first number is unavailable\n");
else if((((y.l>>23)&0x000000FF)==0) || (((y.l>>23)&0x000000FF)==0x000000FF))
printf("The second number is unavailable\n");
else{
switch(mul()){
case 1:printf("Overflow(%f)\n",x.f*y.f);break;
case -1:printf("Underflow(%f)\n",x.f*y.f);break;
default:break;
}
}
}
return 0;
}