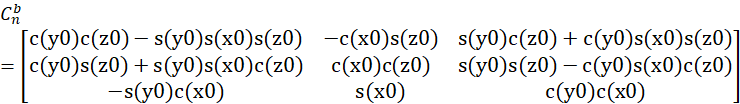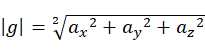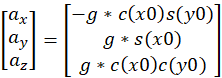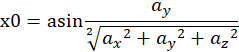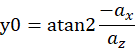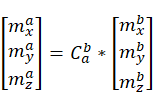由磁场数据和加速度数据计算初始姿态角

前言

        一般惯导姿态角的初始值是由加速度数据和磁场数据计算得到的，加速度数据计算得到滚转角和俯仰角，由滚转角，俯仰角以及磁场数据经过计算再得到初始的偏航角。下面是具体的计算和推导过程。

计算过程:

1.计算滚转角和俯仰角

        这里我们的导航坐标系为东北天坐标系（ENU），载体坐标系为右、前，上（x,y,z）,姿态角的旋转顺序为：z,x,y(偏航、俯仰，滚转)。

对于加速度计，有以下公式：

                                                                            

 

表示导航系到载体系的转换矩阵。设偏航、俯仰，滚转的初始值分别为z0 ，y0 , x0 。

 

并且满足： 

经过计算得到:

                                                                        

所以：

                                                             

                                                                       

 

在推导过程中纯手推容易出错，可以借助matlab计算矩阵，这样不易出错，我在推导这部分时也使用matlab来计算。代码如下：

syms x0  
syms y0  
syms z0
syms g   
 
x_r_matrix=[1,0,0;0,cos(x0),-sin(x0);0,sin(x0),cos(x0)];
y_r_matrix=[cos(y0),0,sin(y0);0,1,0;-sin(y0),0,cos(y0)];
z_r_matrix=[cos(z0),-sin(z0),0;sin(z0),cos(z0),0;0,0,1];
Cn_b = z_r_matrix*x_r_matrix*y_r_matrix; 
Cb_n = Cn_b'; 
g_n=[0;0;g];
g_b=Cb_n*g_n;

2.计算偏航角

这块可以想象一下，假设一开始平稳放置磁力计，则偏航角的计算公式如下：

                                                                                  

该平稳状态设定为a状态，即俯仰角和滚转都为0,对于磁力计放置的任意状态，有以下公式：

                                                                                   

 

                                                     

 

                                              

 

根据上式求出 和 之后，再根据 公式就可求出偏航角。

Matlab推导代码如下：

syms x0  
syms y0   
syms z0    
syms mgbx  
syms mgby   
syms mgbz    
 
x_r_matrix=[1,0,0;0,cos(x0),-sin(x0);0,sin(x0),cos(x0)];
y_r_matrix=[cos(y0),0,sin(y0);0,1,0;-sin(y0),0,cos(y0)];
z_r_matrix=[1,0,0;0,1,0;0,0,1];
Cn_b = z_r_matrix*x_r_matrix*y_r_matrix; m_b=[mgbx;mgby;mgbz]; 
m_n = Cn_b*m_b;

 

实际验证

我这里验证使用的IMU型号为ADI公司的ADIS16470，其载体坐标系的定义如下图所示：

                                                  

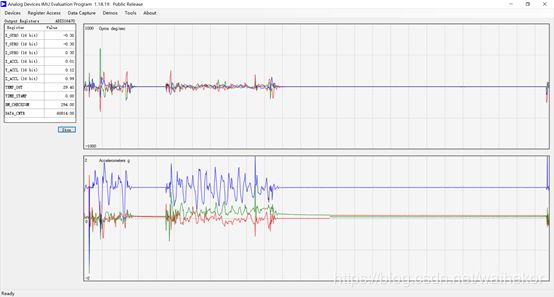
和上文提到的载体坐标系是一致的，右，前，上代表载体坐标系的x,y,z轴，软件界面如下图所示：

                                

        具体的验证过程很简单，这里不再详叙，不同IMU的载体坐标系定义是不一样的，这点在使用时要注意。当逆时针绕y轴旋转，x轴数据为负， z轴向数据为正；当顺时针绕y轴旋转，x轴向数据为正，z轴数据为正；当逆时针绕x轴旋转，y轴数据为正，z轴数据为正；当顺时针绕x轴旋转，y轴数据为负，z轴数据为正。和前面公式计算得到的角度的正负号验证是一致的。

参考文献

1. Euler angles, quaternions, and transformation matrices for space shuttle analysis
2. A Double Stage Kalman Filter for Orientation Tracking With an Integrated Processor in 9D IMU