用PCA,LDA,KNN对MNIST数据集分类（Python）

主成分分析
对于高维空间中$x$, 我们寻求线性变换，
$$y=W^{T}x,wherex\in {\mathbb{R}}^n,W\in {\mathbb{R}}^{m\times d},y\in {\mathbb{R}}^d,d<m.$$
我们采用可重构性观点， 即样本到此超平面的距离都足够近。\
假设投影变换是正交变换，设样本点 $x_i$ 在新坐标系下的坐标为：
$$y_i=(y_{i1},y_{i2},\cdots ,y_{id}{)}^T\in {\mathbb{R}}^d$$
于是在新的坐标系下， $x_i$ 的新表示为
$${\hat{x}}_i=\sum _{j=1}^d{y}_{ij}{w}_j,j=1,2,\cdots ,n.$$经计算我们有
$$\sum _{i=1}^n\Vert x-{\hat{x}}_i{\Vert }_2^2=-\mathbf{T}\mathbf{r}\left(W^T\sum _{i=1}^n{x}_i{x}_i^{T}W\right)+const$$故我们的优化问题转化为
$$\underset{\mathbf{W}\in {\mathbb{R}}^{m\times d}}{\max }\mathbf{T}\mathbf{r}\left({\mathbf{W}}^{\mathbf{T}}\mathbf{X}{\mathbf{X}}^{\mathbf{T}}\mathbf{W}\right),s.t.\mathbf{W}{\mathbf{W}}^{\mathbf{T}}=\mathbf{I}.$$
采用拉格朗日乘子法，经过矩阵计算我们有
$$\mathbf{X}{\mathbf{X}}^{\mathbf{T}}\mathbf{W}=\lambda \mathbf{W},$$
只需要对协方差矩阵 $\mathbf{X}{\mathbf{X}}^{\mathbf{T}}$ 进行特征值分解， 并对特征值进行排序， 取前 $d$ 个特征值对应的特征向量构成变换矩阵 $\mathbf{W}$。

线性判别分析

给定样本集 $D=\{({\mathbf{x}}_1,y_1),({\mathbf{x}}_2,y_2),\cdots ,({\mathbf{x}}_{\mathbf{n}},y_n)\},y_i\in \{0,1\},$ 令 ${\mathbf{X}}_i,{\mathbf{\mu }}_i,{\mathbf{\Sigma }}_i$ 分别表示第 $i\in \{0,1\}$ 类的示例集合,，均值向量，协方差矩阵。考虑线性变换 $y={\mathbf{w}}^{\mathbf{T}}x$，对两类样本的中心点，在直线上的投影分别为 ${{\mathbf{w}}^{\mathbf{T}}\mathbf{\Sigma }}_0\text{w}$ 和 ${{\mathbf{w}}^{\mathbf{T}}\mathbf{\Sigma }}_1\text{w}$.
欲使同类样本的投影点尽可能接近， 可以让同类样本的协方差尽可能小，即$${\mathbf{w}}^T{\mathbf{\Sigma }}_0\mathbf{w}+{{\mathbf{w}}^{\mathbf{T}}\mathbf{\Sigma }}_1\mathbf{w}尽可能小;$$欲使异类样本的投影点尽可能远离，则可让类中心之间的距离尽可能大，即$$\Vert {{\mathbf{w}}^{\mathbf{T}}\mathbf{\mu }}_0-{{\mathbf{w}}^{\mathbf{T}}\mathbf{\mu }}_1{\Vert }_2^2尽可能大.$$
于是, 我们可以最大化如下函数
$$J(W)=\frac{\Vert {{\mathbf{w}}^{\mathbf{T}}\mathbf{\mu }}_0-{{\mathbf{w}}^{\mathbf{T}}\mathbf{\mu }}_1{\Vert }_2^2}{{{\mathbf{w}}^{\mathbf{T}}\mathbf{\Sigma }}_0\mathbf{w}+{{\mathbf{w}}^{\mathbf{T}}\mathbf{\Sigma }}_1\mathbf{w}}=\frac{{\mathbf{w}}^{\mathbf{T}}({\mathbf{\mu }}_0-{\mathbf{\mu }}_1)({\mathbf{\mu }}_0-{\mathbf{\mu }}_1{)}^{\mathbf{T}}\mathbf{w}}{{\mathbf{w}}^{\mathbf{T}}({\mathbf{\Sigma }}_0+{\mathbf{\Sigma }}_1)\mathbf{w}}$$
我们定义类内散度矩阵$${\mathbf{S}}_w={\mathbf{\Sigma }}_0+{\mathbf{\Sigma }}_1=\sum _{\mathbf{x}\in X_0}(\mathbf{x}-{\mathbf{\mu }}_0)(\mathbf{x}-{\mathbf{\mu }}_0{)}^T+\sum _{\mathbf{x}\in X_1}(\mathbf{x}-{\mathbf{\mu }}_1)(\mathbf{x}-{\mathbf{\mu }}_1{)}^T$$
定义类间散度矩阵
$${\mathbf{S}}_b=({\mathbf{\mu }}_0-{\mathbf{\mu }}_1)({\mathbf{\mu }}_0-{\mathbf{\mu }}_1{)}^T,$$
此时目标函数可以写为\textbf{广义Rayleigh熵}:
$$J(w)=\frac{{\mathbf{w}}^{\mathbf{T}}{\mathbf{S}}_b\mathbf{w}}{{{\mathbf{w}}^{\mathbf{T}}\mathbf{S}}_w\mathbf{w}}.$$ 由于目标函数值与长度无关， 故上述问题可转化为
$$\max {\mathbf{w}}^T{\mathbf{S}}_b\mathbf{w},s.t.{\mathbf{w}}^T{\mathbf{S}}_w\mathbf{w}=1.$$
由拉格朗日乘子法， 有
$${\mathbf{S}}_b\mathbf{w}=\lambda {\mathbf{S}}_w\mathbf{w}\Rightarrow {\mathbf{S}}_w^{-1}{\mathbf{S}}_b\mathbf{w}=\lambda \mathbf{w}.$$
代入计算有
$$\mathbf{w}={\mathbf{S}}_w^{-1}({\mathbf{\mu }}_0-{\mathbf{\mu }}_1).$$
上述是两类LDA算法， 我们将其稍加推广，便得到了我们下面问题中将会使用的多类LDA算法， 设类别数为 $c$, 定义全局散度矩阵
$${\mathbf{S}}_t={\mathbf{S}}_w+{\mathbf{S}}_b=\sum _{i=1}^n({\mathbf{x}}_i-\mathbf{\mu })({\mathbf{x}}_i-\mathbf{m}\mathbf{u}{)}^T,\mathbf{\mu }=\sum _{i=1}^n{\mathbf{x}}_i;$$
定义类间散度矩阵$${\mathbf{S}}_w=\sum _{j=1}^c{\mathbf{S}}_{wj},S_{wj}=\sum _{\mathbf{x}\in X_j}(\mathbf{x}-{\mathbf{\mu }}_j)(\mathbf{x}-{\mathbf{\mu }}_j{)}^T,{\mathbf{\mu }}_j=\frac{1}{n_j}\sum _{\mathbf{x}\in {\mathbf{X}}_{\mathbf{j}}}\mathbf{X};$$
定义类间散度矩阵
$${\mathbf{S}}_b={\mathbf{S}}_t-{\mathbf{S}}_w=\sum _{j=1}^c{n}_j({\mathbf{\mu }}_j-\mathbf{\mu })({\mathbf{\mu }}_j-\mathbf{\mu }{)}^T,$$
我们求解下述优化问题
$$\max \frac{\mathbf{T}\mathbf{r}\left({\mathbf{W}}^T{\mathbf{S}}_b\mathbf{W}\right)}{\mathbf{T}\mathbf{r}\left({{\mathbf{W}}^{\mathbf{T}}\mathbf{S}}_w\mathbf{W}\right)},s.t.{\mathbf{W}}^{\mathbf{T}}\mathbf{W}=\mathbf{I}.$$

MNIST数据集

我们采用pytorch 来实现代码， 首先加载 MNIST 数据集，

# mnist classification
import torch
import torchvision
import numpy as np
from sklearn.decomposition import PCA
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA
from sklearn.neighbors import KNeighborsClassifier
from sklearn.preprocessing import MinMaxScaler
import matplotlib.pyplot as plt
import time
'''download mnist dataset '''
train_loader = torch.utils.data.DataLoader(
    torchvision.datasets.MNIST('mnist_data', train=True, download=True,
                               transform=torchvision.transforms.Compose([
                                   torchvision.transforms.ToTensor()
                               ])),
    shuffle=True)
test_loader = torch.utils.data.DataLoader(
    torchvision.datasets.MNIST('mnist_data', train=False, download=True,
                               transform=torchvision.transforms.Compose([
                                   torchvision.transforms.ToTensor()
                               ])),
    shuffle=False)

对上述数据集稍作处理，（归一化）

X_train = train_loader.dataset.train_data.view(60000, 28*28).numpy()
X_train_label = train_loader.dataset.train_labels.numpy()
X_test = test_loader.dataset.test_data.view(10000, 28*28).numpy()
X_test_label = test_loader.dataset.test_labels.numpy()
print('Train:', X_train.shape, 'Label:', X_train_label.shape)
# Train: (60000, 784) Label: (60000,)
mms = MinMaxScaler()
X_train = mms.fit_transform(X_train)
X_test = mms.fit_transform(X_test)

PCA降维：我们将维数分为5个部分，【50,100,200,300,400】（经过PCA之后的维数）
KNN(k近邻算法）中近邻个数取1，3
LDA:降维维数需要讨论。我们以k近邻数为3，PCA维数为50，观测不同LDA维数对应的分类精度，如下图：

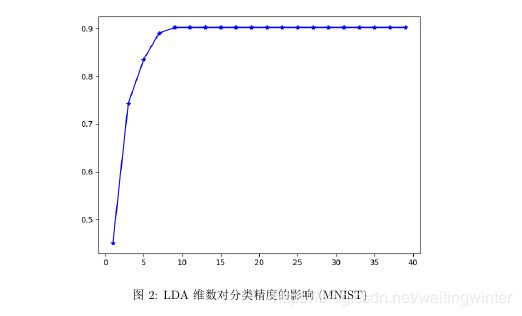
故我们取LDA降维后的维数是PCA降维后维数的1/2,进行测试

'''PCA Dimensionality Reduction'''
# 原始数维数为784，降维后的维数为N1,实际取N1={50,100,200,300,400}
M1 = np.array([50, 100, 200, 300, 400])
M2 = np.array([1, 3])
accuracy = np.zeros([5, 2])
time1 = np.zeros([5, 2])
accuracy_no = np.zeros([5, 2])
time_no = np.zeros([5, 2])
for i in range(len(M1)):
    for j in range(len(M2)):
        N1 = M1[i]
        N2 = M2[j]
        pca = PCA(n_components=N1)
        pca.fit(X_train)
        train_data_pca = pca.transform(X_train)
        test_data_pca = pca.transform(X_test)
        knn = KNeighborsClassifier(n_neighbors=N2, p=2, metric='minkowski')
        mms = MinMaxScaler()
        N2 = N1 / 2
        start_time = time.time()
        lda = LDA(n_components=N2)
        lda.fit(train_data_pca, X_train_label)
        train_data_lda = lda.transform(train_data_pca)
        test_data_lda = lda.transform(test_data_pca)

        train_data_lda_std = mms.fit_transform(train_data_lda)
        knn.fit(train_data_lda_std, X_train_label)
        test_pred = knn.predict(mms.fit_transform(test_data_lda))
        time1[i][j] = time.time() - start_time
        accuracy[i][j] = np.mean(np.equal(test_pred, X_test_label))

        start_time = time.time()
        train_data_lda_std = mms.fit_transform(train_data_pca)
        knn.fit(train_data_lda_std, X_train_label)
        test_pred = knn.predict(mms.fit_transform(test_data_pca))
        time_no[i][j] = time.time() - start_time
        accuracy_no[i][j] = np.mean(np.equal(test_pred, X_test_label))
plt.figure()
plt.plot(M1, accuracy[:, 0], M1, accuracy[:, 1], M1, accuracy_no[:, 0], M1, accuracy_no[:, 1])
plt.legend(['k=1', 'k=3', 'k=1,without LDA', 'k=3,without LDA'])
plt.show()

plt.figure()
plt.plot(M1, time1[:, 0], M1, time1[:, 1], M1, time_no[:, 0], M1, time_no[:, 1])
plt.legend(['k=1', 'k=3', 'k=1,without LDA', 'k=3,without LDA'])
plt.show()

结果如图所示


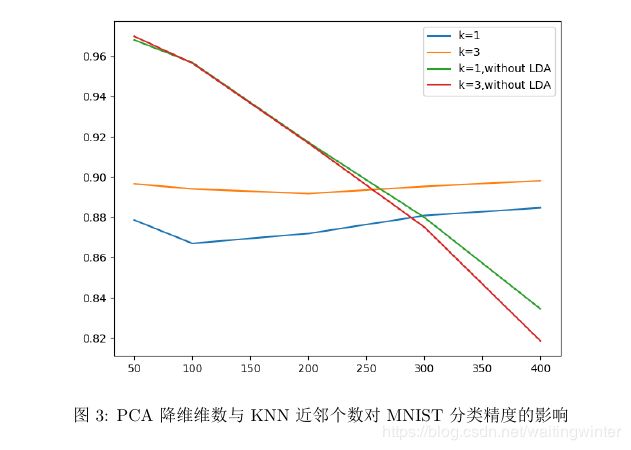
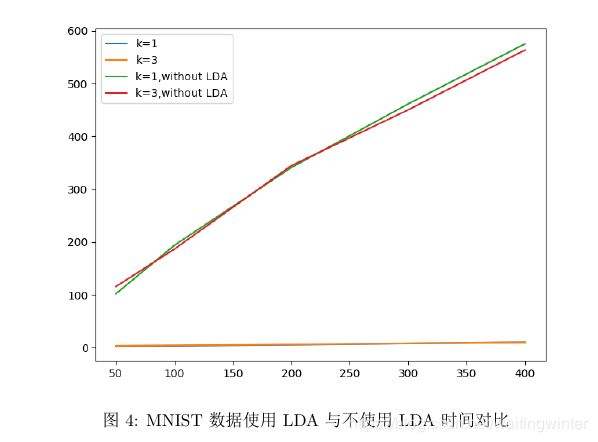
从图(3)中可以看出, $k=3$ 时分类结果比 $k=1$ 时的分类结果好，不使用LDA降维比使用LDA降维的分类结果好。 使用LDA降维后，分类准确率在 $0.87\sim 0.91$ 之间； 不使用 LDA 降维后，分类准确率在0.96左右。 在数值实验过程中，我们发现，尽管不使用LDA精度更高，但是运行的时间大大增加， 具体见图(4)
注意：此程序运行时间半个小时以上，原因见图（4），读者可将代码中不使用LDA部分去掉，之后运行时间应该在几分钟内
最后，给出一个PCA,LDA，KNN实现的程序

from sklearn.decomposition import PCA
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA
from sklearn.neighbors import KNeighborsClassifier
from sklearn.preprocessing import MinMaxScaler

pca = PCA(n_components=N1)
pca.fit(X_train)
train_data_pca = pca.transform(X_train)
test_data_pca = pca.transform(X_test)

lda = LDA(n_components=N1)
lda.fit(train_data_pca, X_train_label)
train_data_lda = lda.transform(train_data_pca)
test_data_lda = lda.transform(test_data_pca)

knn = KNeighborsClassifier(n_neighbors=N2, p=2, metric='minkowski')
mms = MinMaxScaler()
train_data_lda_std = mms.fit_transform(train_data_lda)
knn.fit(train_data_lda_std, X_train_label)
test_pred = knn.predict(mms.fit_transform(test_data_lda))