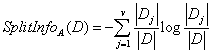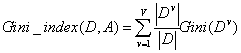ID3、C4.5、CART决策树介绍

决策树是一类常见的机器学习方法，它可以实现分类和回归任务。决策树同时也是随机森林的基本组成部分，后者是现今最强大的机器学习算法之一。

1. 简单了解决策树

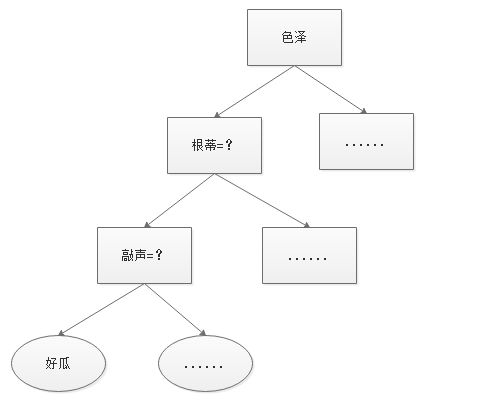
举个例子，我们要对”这是好瓜吗？”这样的问题进行决策时，通常会进行一系列的判断：我们先看”它是什么颜色的”，如果是”青绿色”， 我们再看”它的根蒂是什么形态”，如果是”蜷缩”，我们再判断”它敲起来是什么声音”，最后我们判断它是一个好瓜。决策过程如下图所示。 

 

 

决策过程的最终结论对应了我们所希望的判定结果，”是”或”不是”好瓜。上图就是一个简单的决策树。

那么我们就会有疑问了，为什么这棵树是这样划分的呢？一定要以”色泽”作为根节点吗？对此，就需要划分选择最优的属性。

 

2. 划分选择

一般而言，我们希望决策树的分支节点所包含的样本尽可能属于同一类别，即结点的”纯度”越高越好。常用的纯度有”信息增益”、 ”信息增益率”、 ”基尼指数”或”均方差”，分别对应ID3、C4.5、CART。

 

3. ID3决策树

3.1 信息熵

信息熵是度量样本集合纯度最常用的一种指标。假定当前样本集合 中第类样本所占的比例为，则D的信息熵定义为：

其中p_i是数据集D中任意样本属于类C_i的概率，用 估计。

Info(D)的值越小，D的纯度越高。

 

3.2 条件熵

当前样本集中，考虑到不同的分支结点所包含的样本数不同，可以赋予不同的权重，样本数越多的分支结点对应的影响越大，即为条件熵，定义如下：

其中，充当第j个划分的权重。

 

3.3 信息增益

信息增益 = 信息熵 – 条件熵，即

当信息熵一定时，条件熵越小（即纯度越大），信息增益越大，选择信息增益最大的属性作为最优划分属性。

 

3.4 算法过程

输入：训练集 ;

  属性集 

(1)  生成结点node；

训练集：

属性集：

(2)  如果数据集D都属于同一个类C，那么将node标记为C类叶子结点，结束；

(3)  如果数据集D中没有其他属性可以考虑，那么按照少数服从多数的原则，在node上标出数据集D中样本数最多的类，结束；

(4)  否则，根据信息增益，选择一个信息增益最大的属性作为结点node的一个分支。

(5)  结点属性选定后，对于该属性中的每个值：

a)     每个值生成一个分支，并将数据集中与该分支有关的数据收集形成分支结点的样本子集D_v，删除结点属性那一栏；

b)     如果D_v非空，则转(1)，运用以上算法从该结点建立子树。

 

4. C4.5决策树

信息增益准则偏向于可取值数目较多的属性（例如：将”编号”作为一个划分属性，那么每个”编号”仅包含一个样本，分支结点的纯度最大，条件熵为0，信息增益=信息熵，信息增益达到最大值），为减少这种偏好带来的不利影响，使用了”信息增益率”来选择最优划分属性。

4.1 信息增益率

信息增益率是在信息增益的基础上，增加了属性A的信息熵。

信息增益率的定义如下：

 

其中

 

该值表示数据集D按属性A分裂的v个划分产生的信息。

注意：信息增益率偏向于可取值数目较少的属性，所以C4.5算法不是直接选择增益率最大的划分属性，而是先从划分属性中找出信息增益高于平均水平的属性，再从中选择信息增益率最高的属性。

 

4.2 算法过程

输入：

 

训练集 

属性集 

(1)  生成结点node；

(2)  如果数据集D都属于同一个类C，那么将node标记为C类叶子结点，结束；

(3)  如果数据集D中没有其他属性可以考虑，那么按照少数服从多数的原则，在node上标出数据集D中样本数最多的类，结束；

(4)  否则，根据信息增益率，先从划分属性中找出信息增益高于平均水平的属性，再从中选择信息增益率最高的属性。作为结点node的一个分支。

(5)  结点属性选定后，对于该属性中的每个值：

a)     每个值生成一个分支，并将数据集中与该分支有关的数据收集形成分支结点的样本子集D_v，删除结点属性那一栏；

b)     如果D_v非空，则转(1)，运用以上算法从该结点建立子树。

 

5. CART决策树

CART树又名分类回归树，可用于分类和回归。

5.1 基尼指数

分类时数据集的纯度可以用基尼值来度量：

 

纯度越大，基尼值越小。

属性A的基尼指数定义如下：

选择基尼指数最小的属性作为最优划分属性。

5.2  均方差

回归时数据集D的纯度可以用均方差来度量：

其中

选择均方差最小的属性作为最优划分属性。

5.3 算法过程

同上，第(4)步中计算”信息增益率”改为”基尼指数”或”均方差”即可。

 

6. 算法比较

算法	支持模型	树结构	特征选择	连续值处理	缺失值处理	剪枝	特征属性多次使用
ID3	分类	多叉树	信息增益	不支持	不支持	不支持	不支持
C4.5	分类	多叉树	信息增益率	支持	支持	支持	不支持
CART	分类、回归	二叉树	基尼系数、均方差	支持	支持	支持	支持

 

7. 决策树优缺点

优点：

• 推理过程容易理解，计算简单，可解释性强。
• 比较适合处理有缺失属性的样本。
• 可自动忽略目标变量没有贡献的属性变量，也为判断属性变量的重要性，减少变量的数目提供参考。

缺点：

• 容易造成过拟合，需要采用剪枝操作。
• 忽略了数据之间的相关性。
• 对于各类别样本数量不一致的数据，信息增益偏向于那些更多数值的特征。

 

8. 决策树适用情景

• 决策树能够生成清晰的基于特征选择不同预测结果的树状结构，数据分析师希望更好的理解手上的数据的时候可以使用。
• 决策树更大的作用是作为一些更有用的算法的基石。例如：随机森林、AdaBoost、GBDT。

 

以上为决策树的介绍说明，后续讲解C4.5和CART树的连续值处理、缺失值处理、剪枝，敬请期待！

转载于:https://www.cnblogs.com/cymx66688/p/10691933.html