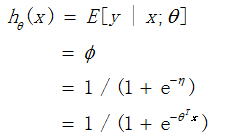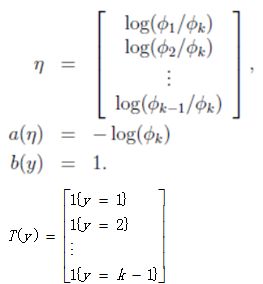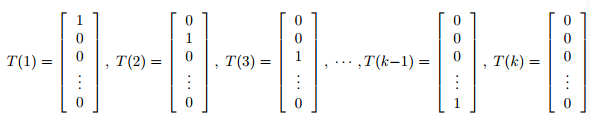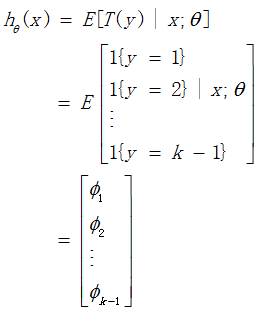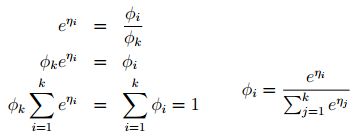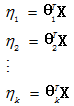广义线性模型(Generalized Linear Model)
http://www.cnblogs.com/sumai
1.指数分布族
我们在建模的时候,关心的目标变量Y可能服从很多种分布。像线性回归,我们会假设目标变量Y服从正态分布,而逻辑回归,则假设服从伯努利分布。在广义线性模型的理论框架中,则假设目标变量Y则是服从指数分布族,正态分布和伯努利分布都属于指数分布族,因此线性回归和逻辑回归可以看作是广义线性模型的特例。那什么是指数分布族呢?若一个分布的概率密度或者概率分布可以写成这个形式,那么它就属于指数分布族。
![]()
其中,η成为分布的自然参数(nature parameter);T(y)是充分统计量(sufficient statistic),通常T(y)=y。当参数 a、b、T 都固定的时候,就定义了一个以η为参数的函数族。
2.广义线性模型(GLM)
下面我们看 GLM 的形式化定义,GLM 有三个假设:
- (1)y| x; θ 满足一个以η为参数的指数分布,那么可以求得η的表达式。
- (2) 给定x,我们的目标是要预测T(y)的期望值,大多数情况下T(y) = y,那么我们实际上要确定一个h(x),使得h(x)=E[y| x]。
- (3)η=θTx。(如果η是向量,那么ηi=θTix)
以逻辑回归作简单的例子说明,首先Y服从伯努利分布,并且写成指数分布族形式,Φ是Y=1的概率。
接着我们可以发现,T(y)=y, Φ =1/(1 + e−η)
η以不同的映射函数与其它概率分布函数中的参数发生联系,从而得到不同的模型,广义线性模型正是将指数分布族中的所有成员(每个成员正好有一个这样的联系)都作为线性模型的扩展,通过各种非线性的连接函数将线性函数映射到其他空间,从而大大扩大了线性模型可解决的问题。
3. Softmax Regression
Softmax Regression是GLM的另外一个例子。假设预测值 y 有 k 种可能,即 y∈{1,2,…,k}。比如 k=3 时,可以看作是要将一封未知邮件分为垃圾邮件、个人邮件还是工作邮件这三类。
- 步骤一:
假设y服从推广的伯努利分布(多项式分布中n=1的情况),总共有k个类别,用k-1个参数![]() 代表y属于每一类的概率。
代表y属于每一类的概率。
接着,我们要把y的分布写成指数分布族的形式。首先,先考虑伯努利分布的表达式为:![]() ,这是y只有两个分类的情况。现在,我们的y有k个情况,这是我们引入一个示性函数1{.}(1{True} = 1, 1{False} = 0)。
,这是y只有两个分类的情况。现在,我们的y有k个情况,这是我们引入一个示性函数1{.}(1{True} = 1, 1{False} = 0)。
- 步骤二:
这时候,T(y)是一组 k-1 维的向量,不再是 y,如下所示:
构建hθ(x)
再用自然参数η来表示Φ
- 步骤三:
最后,用特征的线性组合去表示自然参数。
那么就建立了假设函数,最后就获得了最大似然估计
对该式子可以使用梯度下降算法或者牛顿方法求得参数θ后,使用假设函数h对新的样例进行预测,即可完成多类分类任务。对于互斥的多分类问题,这种模型比较合适,而对于非互斥的多分类问题,构建k个one-vs-all逻辑回归模型更为合适。