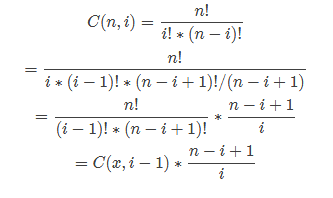2014-2015 ACM-ICPC, Asia Xian Regional Contest（部分题解）

摘要

　　本文主要给出了2014-2015 ACM-ICPC, Asia Xian Regional Contest的部分题解，说明了每题的题意、解题思路和代码实现，意即熟悉区域赛比赛题型。

---

 

Built with Qinghuai and Ari Factor

题意

判断是否是Q数列，只要数列中每个数均能够被3整除就是Q数列。

解题思路

需要特判一下0的情况。

代码

 1 #include 
 2 
 3 int main()
 4 {
 5     int T;
 6     int n;
 7     int t = 1;
 8     scanf("%d", &T);
 9     while(T--) {
10         scanf("%d", &n);
11         int f = 0;
12         int x;
13         for(int i = 0; i < n; i++) {
14             scanf("%d", &x);
15             if(x == 0 || x % 3 != 0 )
16                 f = 1;
17         }
18         if(f)
19             printf("Case #%d: No\n",t++);
20         else
21             printf("Case #%d: Yes\n",t++);
22     }
23     return 0;
24 }

Last Defence

题意

　　定义一个序列，前两项是a和b，第三项是前两项之差的绝对值，然后依次类推，问会出现多少个不同的数字。

解题思路

　　首先能够想到的是该数列最终会呈现...,x,0,x,0这样的序列，但是出现过多少个不同的数字呢，其实给出a和b后，不妨将a写成kb + tmp的形式，其中不同的数字个数就是k个，因为每次相减后出现一个（k - 1）* b + tmp，总共有k个，但这只是一组（相当于减到底），下一组就是b = a % b，a = b，直到b等于0的的时候，就可以结束了，最后再加上0这个数字的1个。

　　注意考虑特殊情况，当a == 0 且b != 0 或者 b == 0 且 a ！= 0时 sum = 2；

　　　　　　　　　　　当a = b = 0时，sum = 1；

代码

 1 #include 
 2 typedef long long ll;
 3 
 4 int main()
 5 {
 6     int T, t = 1;
 7     scanf("%d", &T);
 8     ll a, b, tmp, sum;
 9     while(T--) {
10         scanf("%lld %lld", &a, &b);
11         if(a == 0 && b == 0)
12             sum = 1;
13         else if((a == 0 && b != 0) || (a != 0 && b == 0))
14             sum = 2;
15         else {
16             sum = 1;
17             tmp = 1;
18             while(tmp) {
19                 sum += a / b;
20                 tmp = a % b;
21                 a = b;
22                 b = tmp;
23             }
24         }
25         printf("Case #%d: %lld\n", t++, sum);
26     }
27     return 0;
28 }

Color

题意

　　给出n朵花，排成一行，问从m种颜色中挑出k种染色，使得这n朵花使用恰好k种颜色的同时两个相邻的话不同颜色，有多少种不同的方案。

解题思路

　　不难从m中颜色重挑出k中颜色，即C(m, k)。然后计算恰好使用k种颜色去染着n朵花，容易写出C(m, k) * k * (k - 1)^(n - 1)种方法，但是仔细想一下，这计算了最多使用k种颜色染的方案数，包含重复计数，这里就要考虑容斥了，假设最多使用 i 种颜色的方案数为F[i]，那么其中包括了最多使用 i-1 种的，最多使用 i-1 种的里面又包含了最多使用 i-2 种的，以此类推得到

　　ans = C(m, k) * (F[k] - (F[k - 1] - (F[k - 2] - (... - (F[3] - (F[2] - F[1])))))) = C(m, k) * (F[k] - F[k - 1] + F[k - 2] - ... + (-1)^(k - i)F[i] + (-1)^(k -2)F[2] + (-1)^(k - 1)F[1])，其中F[i]根据之前的计算方法等于(-1)^(k - i) * C(k, i) * (k - i)^(n - 1) 。
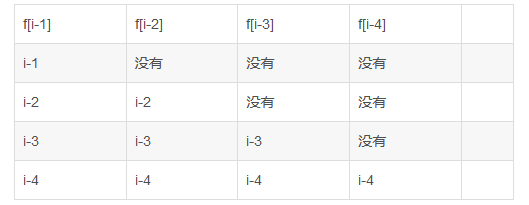
　　也可以看下表

　　

　　如果减去f[i-1]的话，相当于减去整个表格里的内容：一个 i-1, 两个 i-2, 三个 i-3 .....所以因为减去了两个i-2，所以需要把i-2加回来一个，所以  + f[i-2] 就行了，其他同理 ，即可解释容斥原理。举个例子，如果选取的k个颜色是1,2,3,4，会有一种染色方案是1,2,1,2...，如果选取的k-1个颜色是1,2,3，仍然会包含一种染色方案1,2,1,2...所以上面的公式要再加上颜色数<=(k-2)的方案数，然后再减去颜色数<=(k-3)的方案数。

　　剩下的就是具体实现的细节了，首先怎么快速计算C(m, k)和C(k, i)?使用递推的方式，公式推导如下

　　

　　然后其中使用到了乘法逆元。

　　最后就是了解一下输入输出外挂（不加也可以A）。

代码如下

 1 #include 
 2 #include 
 3 
 4 typedef long long ll;
 5 const int mod = 1e9 + 7;
 6 const int maxk = 1e6 + 7;
 7 
 8 ll Sca() {
 9     ll res = 0, f = 0;
10     char x = getchar();
11     if(x == '-')
12         f = 1;
13     if(x >= '0' && x <= '9')
14         res = x - '0';
15     while((x = getchar()) >= '0' && x <= '9')
16         res = res * 10 + (x - '0');
17     return f ? -res : res;
18 }
19 void Out(ll x) {
20     if(x > 9)
21         Out(x / 10);
22     putchar(x % 10 + '0');
23 }
24 ll qpow(ll x, ll n) {
25     ll ans = 1;
26     while(n) {
27         if(n & 1)
28             ans = ans * x % mod;
29         x = x * x % mod;
30         n >>= 1;
31     }
32     return ans;
33 }
34 ll inv[maxk];
35 void get_inv() {
36     for(ll i = 1; i < maxk; i++) {
37         inv[i] = qpow(i, mod - 2);
38     }
39 }
40 ll ck[maxk], cm[maxk];
41 void get_c(ll m, ll k) {
42     cm[0] = ck[0] = 1;
43     for(ll i = 1; i <= k; i++) {
44         cm[i] = (cm[i - 1] * (m - i + 1) % mod) * inv[i] % mod ;
45         ck[i] = (ck[i - 1] * (k - i + 1) % mod) * inv[i] % mod;
46     }
47 }
48 int main()
49 {
50     get_inv();
51     ll T;
52     T = Sca();
53     ll n, m, k;
54     for(ll ca = 1; ca <= T; ca++) {
55         n = Sca();
56         m = Sca();
57         k = Sca();
58 
59         get_c(m, k);
60         ll ans = 0;
61         ll f = 1;
62         for(ll i = k; i >= 1; i--, f = -f) {
63             ans = (ans + (f * ck[i] * i % mod * qpow(i - 1, n - 1) % mod) + mod) % mod;
64         }
65         ans = ans * cm[k] % mod;
66         printf("Case #%lld: %lld\n", ca, ans);
67     }
68     return 0;
69 }

 

Color