017 示例3-天天向上的力量

一、"天天向上的力量"问题分析

1.1 天天向上的力量

基本问题：持续的价值

• 一年365天，每天进步1%，累计进步多少呢？
  • \(1.01^{365}\)
• 一年365天，每天退步1%，累计剩下多少呢？
  • \(0.99^{365}\)

1.2 需求分析

• 数学公式可以求解，似乎没必要用程序
• 如果是"三天打鱼两天晒网"呢？
• 如果是"双休日又不退步"呢？

二、"天天向上的力量"第一问

2.1 问题1： 1‰的力量

• 一年365天，每天进步1%，累计进步多少呢？
  • \(1.01^{365}\)
• 一年365天，每天退步1%，累计剩下多少呢？
  • \(0.99^{365}\)

# DayDayUpQ1.py

dayup = pow(1.001, 365)  # 1.44
daydown = pow(0.999, 365)  # 0.69
print("向上：{:.2f}，向下：{:.2f}".format(dayup, daydown))
# 向上：1.44，向下：0.69

1‰的力量，接近2倍，不可小觑哦

三、"天天向上的力量"第二问

3.1 问题2： 5‰和1%的力量

• 一年365天，每天进步1%，累计进步多少呢？
  • \(1.005^{365}\)，\(1.01^{365}\)
• 一年365天，每天退步1%，累计剩下多少呢？
  • \(0.995^{365}\)，\(0.99^{365}\)

3.1.1 5‰

# DayDayUpQ2.py

dayfactor = 0.005 # 使用变量的好处：一处修改即可
dayup = pow(1+dayfactor, 365)  # 向上：6.17
daydown = pow(1-dayfactor, 365)  # 向下：0.16
print("向上：{:.2f}，向下：{:.2f}".format(dayup, daydown))

5‰的力量，惊讶！

3.1.2 1%

# DayDayUpQ2.py

dayfactor = 0.01 # 使用变量的好处：一处修改即可
dayup = pow(1+dayfactor, 365)  # 向上：37.78
daydown = pow(1-dayfactor, 365)  # 向下：0.03
print("向上：{:.2f}，向下：{:.2f}".format(dayup, daydown))

1%的力量，惊人！

四、"天天向上的力量"第三问

4.1 问题3： 工作日的力量

• 一年365天，一周5个工作日，每天进步1%
• 一年365天，一周2个休息日，每天退步1%
• 这种工作日的力量，如何呢？

1.01365 (数学思维)--》for..in.. (计算思维)

采用循环模拟365天的过程：抽象 + 自动化

# DayDayUpQ3.py

dayup = 1.0
dayfactor = 0.01
for i in range(365):
    if i % 7 in [6, 0]:
        dayup = dayup * (1 - dayfactor)
    else:
        dayup = dayup * (1 + dayfactor)
print("工作日的力量：{:.2f} ".format(dayup))  # 工作日的力量：4.63 

1.001365 = 1.44，1.005365 = 6.17，1.01365 = 37.78 --》 尽管提高1%，但介于1‰和5‰的力量之间

五、"天天向上的力量"第四问

5.1 问题4： 工作日的努力

• 工作日模式要努力到什么水平，才能与每天努力1%一样？
• A君: 一年365天，每天进步1%，不停歇
• B君: 一年365天，每周工作5天休息2天，休息日下降1%，要多努力呢？

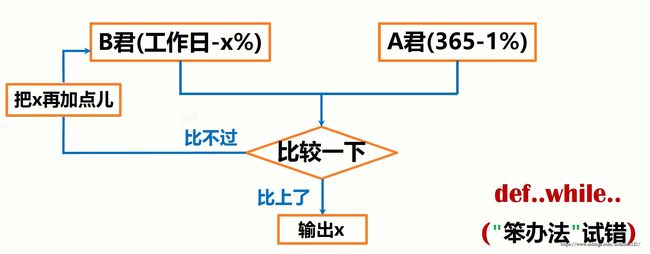
for..in.. (计算思维) --》 def..while.. ("笨办法"试错)

# DayDayUpQ4.py


def dayUP(df):
    dayup = 1
    for i in range(365):
        if i % 7 in [6, 0]:
            dayup = dayup * (1 - 0.01)
        else:
            dayup = dayup * (1 + df)
    return dayup


dayfactor = 0.01
while dayUP(dayfactor) < 37.78:
    dayfactor += 0.001
print("工作日的努力参数是：{:.3f} ".format(dayfactor))  # 工作日的努力参数是：0.019 

根据df参数计算工作日力量的函数

参数不同，这段代码可共用

def保留字用于定义函数

while保留字判断条件是否成立

条件成立时循环执行

\(1.01^{365} = 37.78\)，\(1.019^{365} = 962.89\)

工作日模式，每天要努力到1.9%，相当于365模式每天1%的一倍！

5.2 GRIT

GRIT：perseverance and passion for long-term goals

• GRIT，坚毅，对长期目标的持续激情及持久耐力
• GRIT是获得成功最重要的因素之一，牢记天天向上的力量

六、"天天向上的力量"举一反三

• 实例虽然仅包含8-12行代码，但包含很多语法元素
• 判断条件循环、次数循环、分支、函数、计算思维
• 清楚理解这些代码能够快速入门Python语言

6.1 问题的变化和扩展

• 工作日模式中，如果休息日不下降呢？
• 如果努力每天提高1%，休息时每天下降1‰呢？

• 如果工作3天休息1天呢？

• "三天打鱼，两天晒网"呢？
• "多一份努力"呢？ (努力比下降多一点儿）

• "多一点懈怠"呢？（下降比努力多一点儿）

转载于:https://www.cnblogs.com/nickchen121/p/11183603.html