颓了差不多一周后,决定重开DP
这一周,怎么说,学了学trie树,学了学二叉堆,又学了学树状数组,差不多就这样,然后和cdc一番交流后发现,学这么多有用吗?noip的范围不就是提高篇向外扩展一下,现在向下推进度,该不会写题还是不会,水平能有什么提高,应该老老实实看完DP的所有内容和图论的基本内容,再学学数学,写写oj的题,大概暑假前就干这个吧,累的时候可以去看看莫队和CDQ
然后宣布现在DP内容记录在本章
环形与后效性的处理
例题*1 poj2228
题意:将一天分为N小时,每小时都有一个价值w,有一头牛要睡觉,而它的睡觉是连续的,且第一小时不能算价值,即如果你睡了[a,b],
则你获得的收益是w[a+1]+w[a+2]+……+w[b],而这头牛可以每天多次睡(可以理解成选若干个时间段睡觉),不过每天的睡觉总时间数不能超过B,
求能获得的最大总收益。(不过值得注意的是,“1天”并不是从0~N-1,而可以是从任何一个小时开始到n小时之后,即可以从N-1睡到0)
思考写这道题,很直观的我们用f[i][j]表示前i个小时中,共休息了j个小时,那么我们想,在第i个小时是否睡眠呢,所以我们要再给f数组添一维
f[i][j][0]表示前i个小时中,共休息了j个小时,且第i个小时没有睡
f[i][j][1]表示前i个小时中,共休息了j个小时,且第i个小时睡了
思考怎么写DP方程,
先想一个阶段有多少个状态,答:一共有两个,睡和没睡
然后我们实现转移:
当第i个小时没有睡眠时,根据分析,从前一个阶段到当前阶段,只有两个状态可以转移到这里
f[i,j,0] = max(f[i - 1, j, 1], f[i - 1, j, 0])
当第i个小时睡眠时,同样只有两个状态可以转移到当前阶段
f[i,j,0] = max(f[i - 1, j - 1, 0], f[i - 1, j - 1, 1] + Vi)//Vi表示当前位置睡眠可以获得的收益
初态:f[1,0,0] = 0, f[1,1,1] = 0;
目标:max(f[N,B,1], f[N,B,0])
然后思考解决环的问题
思路一:
从题目我们看到这所谓的一天实际构成了一个环,根据解决环形问题的基本思路,我们把序列在n + 1~n + n + 1再复制一遍
这样从任何一个位置i开始到i + N都算过完了1天
这样我们就相当于把一个环断开变成了一条链(但是我太鶸了不会写,好像也不好写?还是没办法处理本题的特殊情况
思路二:
通过适当的条件和赋值保证与原来的环的情况等价
1.就是上面所推得结果,第一个小时不睡,那么第n个小时就随意了
2.但是为了与原问题情况对照,少了第一个小时在熟睡的情况,因为再原问题的设定中,并不一定第一个小时不能熟睡,所以我们进行第二次DP,强制第一个小时和第n个小时熟睡
最后分别取max值后再取max值
按照思路一,虽然不知道能不能,但是应该解决不了本题的特殊限制,所以我们按照思路二写....
最后考虑初始化的问题:
1、不能全部都memset为-INF:因为f[i][0][0]都被置为-INF,即意味着前i段都不睡是不可能的。
2、不能全部都memset为0:因为像f[i][0][1]这样的状态是不可能发生的,所以必须置为-INF。
3、解决方法:先全部置为-INF,然后在每次循环前把f[i][0][0]置为0。
由于N的范围是[3, 3830],B的范围是[2, N),这样数组至少是3830*3830*2,果断MLE,超内存了。
所以用滚动数组(原来写的mle的,现在修改成ac的qwq)
1 #include
2 #include
3 #include
4 #include
5 #include
6 #include
7 #include
8 using namespace std;
9 const int maxn = 3900;
10 int n, m;
11 int a[maxn];
12 int f[3][maxn][2];
13 inline int read() {//萌萌哒快读呦~(AC了,开心qwq)
14 int x = 0, y = 1;
15 char ch = getchar();
16 while(!isdigit(ch)) {
17 if(ch == '-') y = -1;
18 ch = getchar();
19 }
20 while(isdigit(ch)) {
21 x = (x << 1) + (x << 3) + ch -'0';
22 ch = getchar();
23 }
24 return x * y;
25 }
26 int main() {
27 memset(f, 0xcf, sizeof(f));
28 n = read(), m = read();
29 for(int i = 1; i <= n; ++i)
30 a[i] = read();
31 f[1][0][0] = 0, f[1][1][1] = 0;
32 for(int i = 2; i <= n; ++i)
33 for(int j = 0; j <= min(m, i); ++j) {
34 f[i%2][j][0] = max(f[(i - 1)%2][j][0], f[(i - 1)%2][j][1]);
35 if(j != 0)
36 f[i%2][j][1] = max(f[(i - 1)%2][j - 1][0], f[(i - 1)%2][j - 1][1] + a[i]);
37 }
38 int ans = max(f[n%2][m][1], f[n%2][m][0]);
39 memset(f, 0xcf, sizeof(f));
40 f[1][1][1] = a[1];
41 for(int i = 2; i <= n; ++i)
42 for(int j = 1; j <= min(i, m); ++j) {
43 f[i%2][j][0] = max(f[(i - 1)%2][j][0], f[(i - 1)%2][j][1]);
44 f[i%2][j][1] = max(f[(i - 1)%2][j - 1][0], f[(i - 1)%2][j - 1][1] + a[i]);
45 }
46 ans = max(ans, f[n%2][m][1]);
47 cout << ans <<'\n';
48 return 0;
49 }
例题*2
在一条环形公路旁均匀地分布着N座仓库,编号为1~N,编号为i的仓库与编号为j的仓库之间的距离定义为dist(i,j) = min(|i - j|, N - |i - j|), 也就是逆时针或顺时针从
i到j的中较近的一种。每座仓库都存有货物,其中编号为i的仓库库存量为Ai。在i和j两座仓库之间运输货物需要的代价为Ai+Aj+dist(i,j)。求在哪两座仓库之间运送货物需要的
代价最大。1 <= N <= 10^6
思考在任意位置把环断开,复制一倍接在末尾,形成长度为2N的直线公路。转化之后的问题模型中,公路旁均匀的分布着2N座仓库,其中Ai = A(i+N) (1 <= i <= N)
对于原来环形公路上任意两座仓库i和j(1 <= j < i <= N),如果i - j <= N >> 1,那么在新的公路上,仍然可以对应成在i和j之间运输货物, 代价为Ai + Aj + i - j
如果i - j > N >> 1, 那么可以对应成在i和j + N之间运输货物,代价为Ai + A(j + N) + j + N - i, 其中j + N - i == N - (i - j) <= N >> 1
综上所述,原问题就转化成在长度为2N的直线公路上,满足1 <= j < i <= 2N并且i - j <= N >> 1的哪两座仓库之间运输货物,运送代价Ai + Aj + i - j最大
我们可以枚举i,对于每个i,需要找一个j ∈ [i - N/2, i - 1],使Aj - j尽量大。直观思路二重循环求解
据说单调队列能优化到O(N)....
最后总结一下,对于环形DP,我们一般有两种解决方式,第一种策略就是进行两次DP,第一次在任意位置把环断成链,按照线性DP问题求解,第二次通过适当的条件和赋值,对第一次DP算出的状态进行弥补,保证两次DP最终算出的状态与原问题是等价的。
第二种策略就是在任意位置把环断成链,然后复制一倍接在末尾,对原问题进行适当改变和条件的转化,设定状态进行一次DP。
有后效性的状态转移方程
//只是码下来,基本理解理解......我应该是暂时掌握不了(基本来自李煜东的算法竞赛进阶指南,除了个别是个人理解
//以后学了高斯消元再回来填坑
总最初学习DP时,就一直在强调状态转移方程的无后效性,无后效性是进行动态规划的三前提之一。
但是对于个别题,我们根据题目的关键点抽象出“状态维度”,并设计出状态表示和状态转移方程后,却发现题目却不满足无后效性——部分状态之间互相转移互相影响,构成了环形,无法
确定出一个合适的DP“阶段”,从而沿着某个方向执行递推
事实上,我们可以把状态转移的各状态看作未知量,状态的转移看做若干个方程,如果仅仅是“无后效性”这一条前提不能满足,并且状态转移方程都是一次方程,那么我们可以不进行递推
而是采用高斯消元直接求出状态转移方程的解
【例题】Broken Robot (codeforce24D)
给定一张N*M的棋盘,有一个机器人处于(x,y)位置。这个机器人可以进行很多轮行动,每次等概率地随机选择停在原地,向左走一格,向右走一格或向下走一格。机器人不能移动出棋盘,
求出机器人总起点走到最后一行的任意一个位置,所需的行动次数的数学期望值 1 <= N,M <= 1000
由万能模型传纸条延伸,我们可以想到,对于传纸条,只能向下或是向右,我们用了三个维度
但是这道题有向左,向右或是向下三种走法,甚至可以停在原地,并且是要走到最后一行的任意位置,再按照传纸条的思路设计状态肯定是不行的,那么我们就需要换个思路,我们想传纸
条是如何描述整个状态空间的,传纸条中对于某一条路径,是用路径在当前阶段走到的点的坐标来描述一条路径,对于这个,我们也可以参考,用f[i,j]来表示从点(i,j)走到最后一行所
需行动次数的数学期望值。
状态转移方程比较显然就能得出
1.当机器人在第一列时,显然不能向左走,f[i,1] = 1/3*(f[i,2]+f[i+1,1]+f[i,1]) + 1
2.同理,当机器人在最后一列m时,显然不能向右走,f[i,m] = 1/3*(f[i,m]+f[i+1,m]+f[i,m-1])+1
3.当1 < j < m,即: 2 <= j <= m - 1时,f[i,j] = 1/4*(f[i,j]+f[i+1,j]+f[i,j+1]+f[i,j-1])+1
从上面的方程我们可以看出,从第i行转移到第i+1行时,仍然满足“无后效性”。但是在同一行中,机器人可以向左,可以向右,甚至可以原地不动,各状态之间无法相互转移了,比如某个
点(i,j),在同一行中,他可能是左边扩展来的,也可能是右边扩展来的,甚至可能是他自己扩展来的。我们无法找到一个合理的递推顺序,于是可以使用高斯消元套DP求解(怎么得到这个
结论的??为什么会想到高斯消元(可能是我太弱不知道高斯消元能干什么...))
先以行号为阶段,从N到x倒序扫描每一行。依次计算以该行的每个位置为起点走到最后一行,所需行动次数的数学期望值
然后考虑每行的计算方法。在计算第i行的状态时,因为第i+1行的状态已经已经计算完毕,我们可以把f[i+1,j]看做已知数,于是,状态转移方程中就只剩下f[i,1],f[i,2]...f[i,m]
这个m个未知量,第i行的每一个位置都可以列出一个方程,共m个方程,因此我们可以用高斯消元解出f[i,1],f[i,2]...f[i,m]
于是这个方程就得自己列了...
于是我就不会了...
https://blog.csdn.net/onepointo/article/details/78396567
放一篇博客,csdn的某个不认识的dalao的...希望dalao不要追查到我并锤爆我.....
emmmm差不多先到这吧,剩下的我也不是很懂了....(原来还有概率DP???)
无聊时写题记录:
noip2010乌龟棋
乌龟棋的棋盘是一行N个格子,每个格子上一个分数(非负整数)。棋盘第1格是唯一的起点,第N格是终点,游戏要求玩家控制一个乌龟棋子从起点出发走到终点。
乌龟棋中M张爬行卡片,分成4种不同的类型(M张卡片中不一定包含所有4种类型的卡片,见样例),每种类型的卡片上分别标有1、2、3、4四个数字之一,表示使用这种卡片后
,乌龟棋子将向前爬行相应的格子数。游戏中,玩家每次需要从所有的爬行卡片中选择一张之前没有使用过的爬行卡片,控制乌龟棋子前进相应的格子数,每张卡片只能使用一次。
游戏中,乌龟棋子自动获得起点格子的分数,并且在后续的爬行中每到达一个格子,就得到该格子相应的分数。玩家最终游戏得分就是乌龟棋子从起点到终点过程中到过的所有格子的
分数总和。
很明显,用不同的爬行卡片使用顺序会使得最终游戏的得分不同,小明想要找到一种卡片使用顺序使得最终游戏得分最多。
现在,告诉你棋盘上每个格子的分数和所有的爬行卡片,你能告诉小明,他最多能得到多少分吗?
输入格式:
输入文件的每行中两个数之间用一个空格隔开。
第1行2个正整数N和M,分别表示棋盘格子数和爬行卡片数。
第2行N个非负整数,a1a2……aN,其中ai表示棋盘第i个格子上的分数。
第3行M个整数,b1b2……bM,表示M张爬行卡片上的数字。
输入数据保证到达终点时刚好用光M张爬行卡片。
输出格式:
输出只有1行,1个整数,表示小明最多能得到的分数。
题面翻译:N个格子,每个格子上一个分数,第一个格子是起点,最后一个格子是终点,
有M张卡片,每张卡片有一个数字ai,可向前走ai步(1 <= ai <= 4),并获得走到的格子的分数,求走到终点时,能获得的最大分数
保证从起点走到终点刚好用掉M张卡片
已知n,m,每个格子的分数和M张卡片的数字
显然的线性DP
我们要先划分一下阶段,我们把走到某个位置作为阶段,把走到某个位置所能得到的最大分数作为状态,似乎没有什么问题?
但是我们发现,我们并不是在m个数中随便挑着走的。每张卡片只能选择一次。
重新思考一下,找一个能够覆盖整个状态空间的状态
重新思考我们已知的信息:
1.每个格子的分数,但是这个对于我们设定状态并没有帮助
2.m张卡片和每一张卡片所标记的能够前进的步数,因为数字大于1小于4,所以肯定会有重复,所以我们还可以统计出每种卡片的数量,
只有这些了,我们虽然可以说枚举我们走到了哪个格子,但是我们并不知道还有多少的卡片,某种卡片我们用过多少张,某种卡片我们还能不能用,所以这种思路无法覆盖整个状态空间
最后我们只好把目光放在这m张卡片上,每种卡片的数量是不同的,我们只用一个m是不能笼统的描述状态空间的,然后我们怎么办?我们想,我们能够计算出每种卡片的个数,当我们知道
某个阶段用了多少张卡片时,虽然我们不能知道这几张卡片是什么顺序使用的,但是由于我们是由前一个状态推导过来的,所以我们知道前一个状态怎么使用....逐层向前,最后我们知道
在递推的最初是怎么使用的,但是事实上,我们知道这个是没有用处的,前面每张卡片的使用顺序与我们有什么关系?我们只需要知道每种卡片分别使用了多少多少张时的最大分数就行了
于是我们可以非常粗暴地,用f[a,b,c,d]表示“1”卡片用了a张,“2”卡片用了b张,“3”卡片用了c张,“4”卡片用了d张时,我们能够得到的最大分数,最后当把所有的都用完时,我们肯定
走完了n个格子。
然后我们思考怎么推导过来的:我们想,我们一次显然只能用一张,所以可以有4种方式推导过来
同num[i]表示走到第i个格子时,第i个格子的分数
f[a,b,c,d] = max{f[a,b,c,d-1], f[a,b,c-1,d], f[a,b-1,c,d], f[a-1,b,c,d]} + num[i]
最后思考我们怎么知道目前走到了哪一步,我们当然可以枚举,但是肯定会出锅,这是不行的,但是我们想,我们知道每种牌用了多少张了,我们能够直接计算出我们现在在哪个格子。
用r表示现在在第r个格子,但是在第一个格子时,我们连1张卡片都没用,所以要单独再+1
r = a * 1 + b * 2 + c * 3 + d * 4 + 1
这样我们需要四维数组和四重循环,怕的不敢写,但是我们直接看原题可以知道,数据范围不大,可行的。
初态:因为起点是第一个格子,所以初值为f[0][0][0][0] = num[1];
理清之后就真的好写了
1 #include
2 using namespace std;
3 const int N = 42;
4 int n, m;
5 int f[N][N][N][N], sum[5], num[355];
6 inline int read() {
7 int x = 0, y = 1;
8 char ch = getchar();
9 while(!isdigit(ch)) {
10 if(ch == '-') y = -1;
11 ch = getchar();
12 }
13 while(isdigit(ch)) {
14 x = (x << 1) + (x << 3) + ch - '0';
15 ch = getchar();
16 }
17 return x * y;
18 }
19 int main() {
20 memset(sum, 0, sizeof(sum));
21 n = read(), m = read();
22 for(int i = 1; i <= n; ++i)
23 num[i] = read();
24 for(int i = 1; i <= m; ++i){
25 int cnt;
26 cnt = read();
27 sum[cnt]++;
28 }
29 f[0][0][0][0] = num[1];
30 for(int a = 0; a <= sum[1]; ++a)
31 for(int b = 0; b <= sum[2]; ++b)
32 for(int c = 0; c <= sum[3]; ++c)
33 for(int d = 0; d <= sum[4]; ++d) {
34 int r = a + b * 2 + c * 3 + d * 4 + 1;
35 if(a != 0) f[a][b][c][d] = max(f[a][b][c][d], f[a - 1][b][c][d] + num[r]);
36 if(b != 0) f[a][b][c][d] = max(f[a][b][c][d], f[a][b - 1][c][d] + num[r]);
37 if(c != 0) f[a][b][c][d] = max(f[a][b][c][d], f[a][b][c - 1][d] + num[r]);
38 if(d != 0) f[a][b][c][d] = max(f[a][b][c][d], f[a][b][c][d - 1] + num[r]);
39 }
40 cout << f[sum[1]][sum[2]][sum[3]][sum[4]] <<'\n';
41 return 0;
42 }
倍增优化DP
前两天刚刚填了一下倍增优化递推的坑,现在来学倍增优化DP
我们想,DP大多都是以递推来实现的,那么既然我们能够用倍增优化递推,我们应该也是可以用倍增优化DP的,使用倍增把阶段线性增长优化为成倍増长
然后我们想,我们在倍增学过ST表这个东西,在ST表中,f[i,j]表示子区间[i, i + 2^j - 1]的最大值,那么我们想,要是我们按照DP去写,显然就是线性DP,二维空间存储所有区间情况
但是倍增对其进行了优化,我们想一个大区间,要怎么得到,那么显然是可以由;两个小区间合并而来的。
我们知道f[i,j - 1]表示区间[i, i+2^(j-1)-1]的最值,f[i+(1 << j - 1)][j - 1]表示区间[i + 2^(j-1), i + 2^(j-1) + 2^(j-1) - 1]的最值
思考为什么这两个区间能够合并为大区间?我们在这两个区间,长度都为2^(j - 1),总长度为2 * 2^(j - 1) = 2^j
这样就推出了大区间,两个子区间最大值进行比较得到的较大值肯定也就是大区间的最大值。
所以ST表我们是可以直接按照动态规划的思想,把原来的线性DP,利用倍增将O(N^2)复杂度优化到O(NlogN),把线性DP变成了枚举中间点,由小区间合并到大区间的区间DP
所以你甚至可以把ST表当成倍增优化DP的实例emmmm...
然后...然后基本思想先丢这吧....例题难度太高了QAQ
例题1 : noip2012开车旅行
例题2 : Count The Repetitions
然后头铁的我,用了3~4天,A掉了开车旅游,luogu紫题难度,然后我,睿智的,评难度为NOI(我太弱了QAQ!!!!)
小 A 和小 B 决定利用假期外出旅行,他们将想去的城市从 1 到 N 编号,且编号较小的城市在编号较大的城市的西边,已知各个城市的海拔高度互不相同,记城市 i 的海拔高度为Hi,
城市 i 和城市 j 之间的距离 d[i,j]恰好是这两个城市海拔高度之差的绝对值,即d[i,j] = |Hi− Hj|。 旅行过程中,小 A 和小 B 轮流开车,第一天小 A 开车,之后每天轮换一次。
他们计划选择一个城市 S 作为起点,一直向东行驶,并且最多行驶 X 公里就结束旅行。小 A 和小 B的驾驶风格不同,小 B 总是沿着前进方向选择一个最近的城市作为目的地,而小 A
总是沿着前进方向选择第二近的城市作为目的地(注意:本题中如果当前城市到两个城市的距离相同,则认为离海拔低的那个城市更近)。如果其中任何一人无法按照自己的原则选择目的
城市,或者到达目的地会使行驶的总距离超出 X 公里,他们就会结束旅行。
在启程之前,小 A 想知道两个问题:
1.对于一个给定的 X=X0,从哪一个城市出发,小 A 开车行驶的路程总数与小 B 行驶的路程总数的比值最小(如果小 B 的行驶路程为 0,此时的比值可视为无穷大,且两个无穷大视为相
等)。如果从多个城市出发,小 A 开车行驶的路程总数与小 B 行驶的路程总数的比值都最小,则输出海拔最高的那个城市。
2.对任意给定的 X=Xi和出发城市 Si,小 A 开车行驶的路程总数以及小 B 行驶的路程总数。
输入输出格式
输入格式:
第一行包含一个整数 N,表示城市的数目。
第二行有 N 个整数,每两个整数之间用一个空格隔开,依次表示城市 1 到城市 N 的海拔高度,即 H1,H2,……,Hn,且每个 Hi都是不同的。
第三行包含一个整数 X0。
第四行为一个整数 M,表示给定 M 组 Si和 Xi。
接下来的 M 行,每行包含 2 个整数 Si和 Xi,表示从城市 Si出发,最多行驶 Xi公里。
输出格式:
输出共 M+1 行。
第一行包含一个整数 S0,表示对于给定的 X0,从编号为 S0的城市出发,小 A 开车行驶的路程总数与小 B 行驶的路程总数的比值最小。
接下来的 M 行,每行包含 2 个整数,之间用一个空格隔开,依次表示在给定的 Si和
Xi下小 A 行驶的里程总数和小 B 行驶的里程总数。
这道题已经确定了两个人的开车顺序,从题目中我们可以直观的知道,我们需要对序列做一些预处理,我们需要求出i+1~N之间的最大值,记为ga(i),还需要求出i+1~N之间的次大值,记为
gb(i)
把序列A从小到大排序,然后依次串成一个链表,(双向链表.jpg),排序的同时,建立一个数组B,其中Bi表示原始序列的Ai处于链表的哪一个位置
因为链表是有序的,所以在链表中,指针Bn指向的节点的prev和next分别就是An的前驱和后继,通过比较二者与An的差,就能求出与An最接近的值
然后在链表中删除Bn指向的节点,
然后以同样方式考虑Bn-1的前驱和后继,再删除Bn-1
依此类推,最终求出每个Ai最接近的值
预处理结束后,这样我们就知道在哪个位置该走多少路了,思考解题...
于是对于这个问题,我们已经知道每个城市到离它最近和次近的城市,这样实际上我们只需要在意从哪个城市开始即可,因为城市当我们确定起点时,因为A,B两人开车的顺序是确定的,而且
距离也是确定的,所以最后答案就是确定的。
于是再综合题目,对于这个问题,我们就可以汇总出3个关键信息:行驶的天数,所在的城市,和行驶的长度(或者你也可以说A和B分别行走的距离)
我们要从这3个关键信息中挑出一个当做阶段,我们想当我们知道起点时,再知道行驶的天数,我们肯定能得到现在在哪个城市,以及已经行进了多少,因为显然A,B开车的顺序是确定的
所以我们直接把行驶的天数作为阶段,然后我们其实能够发现,数据比较大,若是我们一各天数一个天数,一个城市,一个城市枚举,肯定会爆,这提醒我们对DP进行优化,找一下本题的阶段
的锅...天数,我们也只能在天数上优化,常理讲我们是我们要对天数进行优化,当然是尽可能的减少枚举的次数,使得能够快速跑完,所以说,上倍增啊。
设f[i,j,k]表示从第j个城市出发,行驶了2^i天后,由第k个人开车,k = 1 or 0, 1表示是A开车,0表示是B开车
初值:f[0,j,0] = ga(j) f[0,j,1] = gb(j)
当 i = 1时,因为2^0是奇数,所以两个人从j出发开2^1天到达的城市,等于k先开2^0天,另一个人1-k再开2^0天到达的城市
f[1,j,k] = f[0, f[0,j,k], 1-k]
当 i > 1时,因为2^(i-1)是偶数,所以前后两半路程都轮到k先开车
f[i,j,k] = f[i-1, f[i-1,j,k], k]
然后还需要再处理一下边界情况
当然,还可以更优,我们可以直接省去最后一维,f[i,j]表示从第i个城市开始,A和B每人开了2^j天所到达的城市
方程变化不大,就是把原方程中第二维提至第一维,第一维放到第二维。
接着是解决问题2,怎么说呢,挺稳的吧,显然的一匹,反正倍增一个很显然但重要的性质,a^i-1 + a^i-1 = a^ia^i-1 + a^i-1 = a^i
套着性质搞一波
设da表示从城市j出发·,两人共行驶2^i天,k先开车,小A行驶的总长度
初值da[0,j,0] = dist(j, ga(j)), da[0,j,1] = 0
当i = 1时,da[1,j,k] = da[0,j,k] + da[0, f[0,j,k], 1-k]
当i > 1时,da[i,j,k] = da[i - 1, j, k] + d[i - 1, f[i - 1, j, k], k];
设db表示从城市j出发,两人共行驶了2^i天,k先开车,小B行驶的路程总长度
初值:db[0,j,0] = 0, db[0,j,1] = dist(j, gb(j))
当 i = 1时,db[1, j, k] = db[0, j, k] + db[0, f[0, f[0, j, k],1 - k];
当 i > 1时,db[i, j, k] = db[i - 1, j, k] +db[i - 1, f[i - 1, j, k], k];
同理,求a,b行的路程也同样可以按照上边那样优化成3维
上述DP算法在O(nlogn)的时间内计算出了所以“行驶天数为2的整数次幂”的状态,接下来我们考虑问题。mxdis(s, x)意为“从城市S最多形式X公里时”时,A,B分别行驶的路程
然后,循环计算从每个起点开始,符合条件的mxdis(i, x),然后手动算a,b的比值,求一个最小的,同时记录从某个城市出发(虽然从题目中看是让输出海拔最高的,但从输出说明中我们
可以了解到,要输出的是起点城市)
然后在O(n)枚举所有起点,手动算出对于给定的si, xi,mxdis(si, xi)是多少。
然后一些特殊情况,嗯在代码中有注释进行说明
1 #include
2 #define ll long long
3 using namespace std;
4 const int maxn = 100086;
5 struct lie {
6 ll v, id, l, r;
7 }e[maxn];
8 int n, m, si;
9 ll na[maxn], nb[maxn];//na表示a要行的,nb表示b要行的
10 ll f[maxn][21], fa[maxn][21], fb[maxn][21];
11 ll p[maxn];
12 ll a = 0, b = 0, x, xi;
13 int l, r, j, ans = 0;
14 double minn = 2147483647;
15 inline bool cmp(lie a, lie b) {
16 return a.v < b.v;}
17 inline bool zuo() {//判断是不是左边近
18 if(!l) return 0;
19 if(!r) return 1;
20 return e[j].v - e[l].v <= e[r].v - e[j].v;
21 }
22 inline int pd(int a, int b) {//如果某个点判断左边离的近,那么我在取次近值时,有两种可能,右边紧挨的数和左边紧挨的数的左边的数 ,若某个点判断右边离的近,同理
23 if(!a) return e[b].id;
24 if(!b) return e[a].id;
25 if(e[j].v - e[a].v <= e[b].v - e[j].v) return e[a].id;
26 return e[b].id;
27 }
28 inline void get(ll x, int p) {//计算从某个城市开始,符合条件的情况下a, b行的距离
29 a = b = 0;
30 for(int i = 18; i >= 0; --i)//为什么要倒序?因为这样最后p就是f[p][0]了,方便23333,为什么是18呢,题目最大范围log(100000)/log(2)约为16点多,保险点弄了18,不然直接算int(1.0*log(n)/log(2))+1也可以
31 if(f[p][i] && (a + fa[p][i] + b + fb[p][i]) <= x) {
32 a += fa[p][i];
33 b += fb[p][i];
34 p = f[p][i];
35 }
36 //cout <
37 if(na[p] && a + b + fa[p][0] <= x) a += fa[p][0];//最后我们会发现,尽管我们一路搞下来,但是对于f[p][0]的情况我们还没有计算,单独处理
38 }
39 int main() {
40 scanf("%d", &n);
41 for(int i = 1; i <= n; ++i) {
42 scanf("%lld", &e[i].v);
43 e[i].id = i;
44 }
45 sort(e + 1, e + n + 1, cmp);
46 for(int i = 1; i <= n; ++i) {
47 e[i].l = i - 1, e[i].r = i + 1;
48 p[e[i].id] = i;
49 }
50 e[1].l = e[n].r = 0;
51 /* for(int i = 1; i <= n; ++i)
52 cout < 53 cout <<'\n';
54 for(int i = 1; i <= n; ++i)
55 cout < 56 cout <<'\n';*/
57 for(int i = 1; i <= n; ++i) {
58 j = p[i], l = e[j].l, r = e[j].r;
59 if(zuo()) nb[i] = e[l].id, na[i] = pd(e[l].l, r);//左边的离得近
60 else nb[i] = e[r].id, na[i] = pd(l, e[r].r);//右边的离得近
61 if(l) e[l].r = r;
62 if(r) e[r].l = l;
63 }
64 /*for(int i = 1; i <= n; ++i)
65 cout <*/
66 for(int i = 1; i <= n; ++i) {
67 f[i][0] = nb[na[i]];//初始化,首先肯定确定是A先开车,初始化为在第i个城市,由a先开车后,到达的城市,此时交由b开车时,要前往的城市
68 fa[i][0] = abs(e[p[i]].v - e[p[na[i]]].v);//A最初开的距离记为当前城市的高度 - 将要前往的城市的高度
69 fb[i][0] = abs(e[p[f[i][0]]].v - e[p[na[i]]].v);//B最初来的距离记为B在A开完后将要前往的城市 - A将要开往的城市
70 }
71 for(int j = 1; j <= 18; ++j)//逐层计算,第2^j天前往的城市i, 具体为什么这么走呢?想想ST表吧
72 for(int i = 1; i <= n; ++i) {
73 f[i][j] = f[f[i][j - 1]][j - 1];
74 fa[i][j] = fa[i][j - 1] + fa[f[i][j - 1]][j - 1];
75 fb[i][j] = fb[i][j - 1] + fb[f[i][j - 1]][j - 1];
76 }
77 /*for(int i = 1; i <= n; ++i)
78 cout << f[i][0] <<' ';
79 cout <<'\n';
80 for(int i = 1; i <= n; ++i)
81 cout << fa[i][0] <<' ';
82 cout <<'\n';
83 for(int i = 1; i <= n; ++i)
84 cout << fb[i][0] <<' ';
85 cout <<'\n';
86 scanf("%lld%d", &x, &m);*/
87 scanf("%lld%d", &x, &m);
88 for(int i = 1; i <= n; ++i) {
89 get(x, i);
90 if(b && 1.0 * a / b < minn) {//我们不保证做完DP后b一定不为0,所以b若是等于0,那做除数可就麻烦了
91 minn = 1.0 * a / b;
92 ans = i;
93 }
94 }
95 printf("%d\n", ans);
96 for(int i = 1; i <= m; ++i) {
97 scanf("%d%lld", &si, &xi);
98 get(xi, si);
99 printf("%lld %lld\n", a, b);
100 }
101 return 0;
102 }
最后总结一下吧...
对于倍增优化的DP算法求解问题是,一般分为两部分。
第一部分是预处理,用“阶段”成倍増长的DP,计算出若干与2的整数次幂相关的代表状态。
第二部分是拼凑,基于“二进制划分思想”用上一步得到的代表状态组合成最终答案(摘抄自《算法竞赛进阶指南》)
数据结构优化DP
拿LCIS问题举例:
该问题在进行阶段的转移时,都需要枚举一个决策,在所有可能情况下取最大或最小值。然而随着DP阶段的增长,该决策的取值范围的霞姐不变,上界每次增大1,更加概括的说明:这个决策
的候选集合只扩大而不缩小,然后我们仅用一个变量维护最值,不断与新加入候选集合的元素比较,即可直接得到最优决策,O(1)执行转移
但是存在更加复杂情况,当一个变量不足以维护决策集合时,我们就要考虑一些比较高级的数据结构,维护DP觉得的候选集合,实现快速的插入元素,删除元素,查询最值等操作,例如:线段树,
树状数组等等...
例题1:poj3171 区间最小值覆盖问题
有一条很长的白色纸带,被划分为一个个长为1的网格,其中第L到第R个网格不慎被染上了黑色墨水。现在有N条胶带,第i条可以覆盖第ai到bi个格子,售价为ci。求用若干条贴纸覆盖纸带上
第L到第R个格子,至少要花费多少价钱
(其实原文是john和cow的故事)
然后问题实际就是:
有N (1 <= N <= 10,000)个区间,求覆盖[L,R](0 <= M <= E <= 86,399)的最小代价.
每个区间的代价为Ci (where 0 <= S <= 500,000).
对于这个问题,我们想用f[x]表示覆盖区间[L, x]的最小代价
先思考不加优化的求解:
先将给出的能够使用的所有区间按照右端点R从小到大排序。
最终我们要求的是只有区间f[L, R],于是想,我们是否能够先把左端点大于R的和右端点小于L的区间剔除掉,这些肯定是用不到的,接下来思考解题
对于某个区间的售价是ci,我们从可以使用的第一个区间开始,思考,由于右端点已经递增排序的,所以我们直接从第一个区间的右端点开始,因为我们想,最后要求花费尽可能的少
思考如何转移:
对于某个位置开始,想扩展到bi,可能这个bi的区间的左端点ai会与已经处理过的区间出现重叠,这是我们设一个x, ai-1 <= x <= bi-1(为什么是ai-1和bi-1呢,由于右端点可能有重合的情况,
所以我们的dp[i]中可能存放的并不是最小覆盖代价,同理,左端点可能是某个区间的另一个右端点)
这样我们可以写一个非常暴力的算法求解完这个问题,方程就是:
f[bi] = min{f[x]} + ci;//因为对于每一个位置,都有最终是被替换为了不同的值,所以我们要挨个枚举
复杂度绝对不低,至少爆了本题是绰绰有余的。所以我们要思考优化
但是我们想啊,对于某个可覆盖的区间[ai, bi],如果在这个区间内已经被标记的最小的价格,都不能比把[ai, bi]覆盖掉的价格ci小,那么显然我们就可以直接把这个区间覆盖为ci,所以
就需要查询区间[ai-1, bi]的最小值,同时f数组会不断发生更新。这是一个带有区间的区间最值问题,所以,使用线段树,就能很稳的在O(logn)时间内执行查询、更新操作,
本题的网格的位置都比较小,所以我们可以直接在[L-1, R]上建立线段树
对于本题,请时刻注意自己在写的是一道DP....
我就是写着写着把它当成一道数据结构,而忘记了自己是在写DP,忘记了自己设置的状态,阶段而疯狂调不出来.....
很重要的教训是,尽管写的是一个板子,也不要忘记对板子加以改正,以确保所寻找的是自己设定的状态,保证自己是在DP......
数据结构只是一个工具...不是不能修改的...不要像我一样zz....
1 #include
2 #define ll long long
3 using namespace std;
4 const int maxn = 100086;
5 const int inf = 19999999;
6 struct node {
7 int minn;
8 }tree[maxn * 4];
9 struct nnde {
10 int l, r, val;
11 }e[maxn];
12 int n, M, E;
13 bool flag = 0;
14 inline bool cmp(nnde a, nnde b) {
15 if(a.l == b.l) return a.r < b.r;
16 return a.l < b.l;
17 }
18 inline int read() {
19 int x = 0, y = 1;
20 char ch = getchar();
21 while(!isdigit(ch)) {
22 if(ch == '-') y = -1;
23 ch = getchar();
24 }
25 while(isdigit(ch)) {
26 x = (x << 1) + (x << 3) + ch - '0';
27 ch = getchar();
28 }
29 return x * y;
30 }
31 inline void maintain(int pos) {
32 int lc = pos << 1, rc = pos << 1 | 1;
33 tree[pos].minn = min(tree[lc].minn, tree[rc].minn);
34 }
35 void build(int pos, int l , int r) {
36 tree[pos].minn = inf;
37 if(l == r) return;
38 int mid = (l + r) >> 1;
39 build(pos << 1, l, mid);
40 build(pos << 1 | 1, mid + 1, r);
41 maintain(pos);
42 }
43 void update(int pos, int aim, int l, int r, int v) {
44 if(l == r) {
45 tree[pos].minn = min(tree[pos].minn, v);
46 return ;
47 }
48 int mid = l + r >> 1;
49 if(aim <= mid)
50 update(pos << 1, aim, l, mid, v);
51 else
52 update(pos << 1 | 1, aim, mid + 1, r, v);
53 maintain(pos);
54 }
55 int query_RMQ_Min(int pos, int L, int R, int l, int r) {
56 if(l > R || r < L) return 0;
57 if(L <= l && r <= R) return tree[pos].minn;
58 int mid = (l + r) >> 1;
59 // return min(query_RMQ_Min(pos << 1, L, R, l, mid), query_RMQ_Min(pos << 1 | 1, L, R, mid + 1, r));
60 // 不要像我一样智障的用正常的线段树标准搜索方式去搜索
61 int vv = inf;
62 if(L <= mid)//当这个区间的左端点小于中点时,我们可以把问题向前推进到中点mid,求得到mid时的最小值vv
63 vv = query_RMQ_Min(pos << 1, L, R, l, mid);
64 if(R > mid)//当右区间大于中点时,说明我们可以向后扩展,我们要在到mid时取得的最小值与mid之后区间的最小值之间取min
65 vv = min(vv, query_RMQ_Min(pos << 1 | 1, L, R, mid + 1, r));
66 return vv;
67 }
68 int main() {
69 n = read(), M = read(), E = read();
70 for(int i = 1; i <= n; ++i)
71 e[i].l = read(), e[i].r = read(), e[i].val = read();
72 sort(e + 1, e + n + 1, cmp);
73 build(1, M - 1, E);
74 int st = M - 1;
75 update(1, st, M - 1, E, 0);
76 for(int i = 1; i <= n; ++i) {
77 if(e[i].l > st + 1) {//不能全部覆盖
78 flag = 1;
79 break;
80 }
81 int vul = query_RMQ_Min(1, e[i].l - 1, e[i].r, M - 1, E);
82 //cout << vul <<' ';
83 update(1, e[i].r, M - 1, E, vul + e[i].val);
84 st = max(st, e[i].r);
85 }
86 if(flag) cout << -1 <<'\n';
87 else cout << query_RMQ_Min(1, E, E, M - 1, E) <<'\n';
88 return 0;
89 }
然后上一道树状数组的例题:(lyd的《算法竞赛进阶指南》真棒!~)
The Battle of Chibi hdoj5542
给定一个长度为N的数列A,求A有多少个长度为M的严格递增子序列。
1 <= M <= N <= 1000,序列中的数的绝对值不超过10^9。因为答案可能很大,只需输出对10^9+7取%后的结果
对于这个问题,还是稳稳的分析吧...
先汇总一下信息:
目前已知的情报:
1.一个数列,与数列中的每一个数
2.数列的长度。
没了,所以对于dp阶段的划分与状态的设定肯定是从这两个信息中提取出的。
对于解出这道题,第一想法是到某个数为止,符合严格单调递增条件的序列有多少
但是我们注意到,题目同时还要求长度为M的严格单调的序列,
这提醒我们,我们可以把长度也计入状态,但是我们肯定不能直白的说到当期位置符合长度为M的序列数,显然这个长度是需要变化的...
于是用f[i,j]表示对于长度为N的A序列扫到第i个数Ai时,长度为j的严格单调递增序列有多少个, 1 <= i <= N, 1 <= j <= M
然后显然我们还需要第三层循环k,0 <= k < i,且Ak < Ai
然后我们想,当前位置满足长度为j的序列数,肯定是由当前位置之前的所以满足长度为j - 1这个条件的转移过来的,也就是说,我们实际要求的是:
在第i个数以前,满足长度为j - 1的严格单调序列中,有多少是能够扩展到第i个位置上的
于是状态转移方程就很显然了
f[i,j] = Σ f[k, j - 1]
暴力的的三重循环就很显然了。
但是显然,O(n^3)的复杂度本题是支持不了的,思考本题有没有什么优化策略
因为为了优化的方便....建议把f[i,j]设定为对于长度为N的A序列扫到第j个数Aj时,长度为i的严格单调递增序列有多少个, 1 <= j <= N, 1 <= i <= M
简单来讲就是把循环次序变一变
然后我们可以发现,当进行内层j和k的循环时,最外层i可以是看做不变的,暂时把i当做一个定值看待
接着观察内层循环,每当j增大1时,k的范围就从0 <= k < j变成了0 <= k < j + 1,也就是多了k = j这一个决策,不是就是,是就只是!只是!
为了这多出来的一个决策集合,我们不得不进行一遍新的循环,从头到尾!
显然这花费了大量的时间,于是我们要找一个能够解决这个问题的方法。
对于每一个决策,我们都可以用一个二元组(Ak, f[i - 1, k])来储存,即:到第k个数时,长度为i - 1的数的个数
于是现在我们需要解决这样的问题:
1.插入一个新的决策,即:在j增加1前,把二元组(Aj, f[i - 1, j])加入集合
2.给定一个值Aj,查询满足Ak < Aj的二元组对应的f[i - 1, k]的和
然后我们可以建立一个树状数组,但是我们能发现的是f[i - 1, k]存的值过大,所以我们要把所有数值离散到[2, N+1]间
设val(x)表示x离散化后的值。特殊地,我们令A0 = -∞,val(A0) = 1
然后在[1, N+1]上建立起树状数组,起初所有值为0
1.对于插入决策的操作,把val(Ak)位置上的值增加f[i - 1, k]
2.对于查询操作,我们计算树状数组中[1, val(Aj) - 1]的前缀和
这样我们能够把复杂度优化为O(MNlogN)
然后这样思路就讲通了...接着...为了维持个人习惯....我要按照最O(n^3)时的状态写代码....
1 #include2 #define ll long long 3 using namespace std; 4 const int p = 1000000007; 5 const int maxn = 1500; 6 int n, T, m; 7 int a[maxn], b[maxn]; 8 int c = 0; 9 int f[maxn][maxn]; 10 inline int read() { 11 int x = 0, y = 1; 12 char ch = getchar(); 13 while(!isdigit(ch)) { 14 if(ch == '-') y = -1; 15 ch = getchar(); 16 } 17 while(isdigit(ch)) { 18 x = (x << 1) + (x << 3) + ch - '0'; 19 ch = getchar(); 20 } 21 return x * y; 22 } 23 inline void add(int i, int x, int y) { 24 for(;x <= n; x += x & -x) f[i][x] = (f[i][x] + y) % p; 25 } 26 inline int ask(int i, int x) { 27 int ans = 0; 28 for(; x; x -= x & -x) ans = (ans + f[i][x]) % p; 29 return ans; 30 } 31 int main() { 32 T = read(); 33 while(T--) { 34 memset(f, 0, sizeof(f)); 35 n = read(), m = read(); 36 for(int i = 1; i <= n; ++i) { 37 a[i] = read(); 38 b[i] = a[i]; 39 } 40 sort(b + 1, b + 1 + n); 41 for(int i = 1; i <= n; ++i) 42 a[i] = lower_bound(b + 1, b + n + 1, a[i]) - b; 43 // a[0] = 0xcf; 44 for(int i = 1; i <= n; ++i) 45 for(int j = 1; j <= m; ++j) { 46 if(j == 1) add(1, a[i], 1); 47 else { 48 int sum = ask(j - 1, a[i] - 1); 49 add(j, a[i], sum); 50 } 51 } 52 int num = ask(m, n); 53 cout << "Case #" << ++c << ':' <<' ' < \n'; 54 } 55 return 0; 56 }'
于是未来的某天,我还要再把这些题捞出来,重写....
笔记(摘抄自《算法竞赛进阶指南》)
最初的LCIS,Poj3171,HDOJ5542 这三个问题是循序渐进的。
这些题目中DP决策的取值范围都可以用简单的不等式来表示。
在LCIS中,不等式只有上界变化且只增大不减小,于是我们采用维护变量的方法
在poj3171中,不等式除了上界不断增大外,下界变化没有规律,此时我们采用了更加灵活的支持区间最值维护的数据结构
在hdoj5542中,取值范围有两个限制条件,一个是关于“数组下标”的位置,一个是关于“数列A的数值”的位置,实际上他们是两种“坐标”。DP循环顺序保证了第一个条件的满足。
对于第二个条件,我们在“数列A”这个“坐标轴”上建立了以F数组中的状态为值的数据结构
总而言之,无论DP决策的限制条件是多是少,我们都要尽量对其进行分离。多维DP在执行内层循环时,把外层循环变量看作定值。状态转移取最优决策时,简单的限制条件用循环顺序处理,
复杂的限制条件用数据结构去维护。
单调队列优化DP
单调队列是借助单调性,及时排除不可能的决策,保持候选集合的高度有效性和秩序性。在单调队列时有一道“最大子序和”的题目,该问题的答案可以形式化表述为
ans = max{s[i] - min {s[j]}(1 - M <= j <= j - 1)}(1 <= i <= N)
此处的i类似于动态规划的状态,而j贼类似于动态规划的决策。
我们从小到大枚举每个i∈[i, N],当i增大1时,j的取值范围[i - M, i - 1]上、下界同时增大1,变为[i - M + 1, i]。这意味着不仅有一个新的决策j = i进入了决策集合,也应该把
过时的决策j = i - M从决策集合中删除。由此我们可以想,单调队列适合优化这种决策取值范围上下界均单调变化,每个决策在候选集合中插入或删除至多一次的问题
例题1
Fence poj1821
有N块木板从左到右排成一行,有M个工匠对这些木板进行粉刷,每块木板至多被粉刷一次。第i个工匠要么不粉刷,要么粉刷包含木板si的,长度不超过Li的连续的一段木板,每粉刷一块可以
得到pi的报酬。求如何安排能使工匠们获得的总报酬最多。1 <= N <= 16000, 1 <= M <= 100
首先是把所有木板按照si从小到大排序,这样每个工匠粉刷的木板一定在上一个工匠粉刷的木板之后
设f[i,j]表示前i个工匠粉刷到前j块木板,工匠能获得多少报酬,这样对于第j块木板有这样三种情况
1.第i个工匠可以什么也不刷,这样此时f[i, j] = f[i - 1, j]
2.第j块木板可以空着不刷, f[i, j] = f[i, j - 1]
3.假设第i个工匠要粉刷第k+1块到第j块木板。根据题意,该工匠粉刷不能超过Li,且必须粉刷Si,所以要满足j - k <0000000000000000000000000000000000000000000000000000000= Li 且 k <= Si - 1,也就是当前工匠能够选择粉刷的范围是Si以前
的部分板子,于是我们想第i个工匠要是能刷后面的木板怎么办??然后我最傻的就是,我又一次忘记了循环的次序....前i个工匠刷完前j块木板显然是把第i个工匠自己能刷的都考虑在j的范围内了
这样我们能得到dp方程 f[i, j] = max{f[i - 1, k] + pi * (j - k)} j - Li <= k <= Si - 1, 同时j >= Si.
很直观的对于前两种情况,我们可以直接进行转移,对于第三种情况,我们需要多加一层循环k,复杂度似乎有点高,然后思考能不能对第三种情况进行优化
常规思路,把i看做一个定值,此时只有内层循环j和决策k,然后观察原方程
f[i, j] = max{f[i - 1, k] + pi * (j - k)} j - Li <= k <= Si - 1, 同时j >= Si.
对原方程进行变换
f[i, j] = max{f[i - 1, k] - pi * k + pi * j}
这样我们能够发现对于所有情况都需要加上pi * j,也就是说对于k来说,j也是一个定值,对于k,pi * j就是一个常量
于是方程可以拆成两部分
1.对于决策变量j, pi * j
2.对于决策变量k, 在忽视j的影响时, f[i - 1, k] - pi * k
即原方程可变成: f[i, j] = pi * j + max{f[i - 1, k] - pi * k}
当j增大时,k的取值上界Si不变,下界增大1,变为j - Li + 1。也就是说对于决策集合,每当j增大1,就会有一个决策k被踢出集合,这样我们就想:
假设两个决策k1和k2,使得k1 < k2 < Si - 1,也就是说当j不断增大时,k1会比k2更早的被踢出集合
若再满足:f[i - 1, k] - pi * k1 <= f[i - 1, k] - pi * k2,则k1就是一个无用的决策,因为对于k1,决策k2不仅比它存活时间长,还比它更优,由此我们就可以维护一个k单调递增
f[i - 1, k] - pi * k单调递减的队列,只有这样队列中的决策才有存在的意义,才有可能在某一个时候成为最优决策.
同时因为k的单调性循环已经帮助维护了,所以只维护f[i - 1, k] - pi * k的单调性即可
这个队列需要支持如下操作:
1.当j增大时,检查队头元素,把小于j - Li的出队
2.当需要查询最优决策时,队头即为所求
3.当需要插入新的决策时,在队尾检查f[i - 1, k] - pi * k的单调性,把无用决策从队尾直接出队,同时把新的决策插入队尾
对于本题来说就是当内层循环开始时(j = Si),建立一个空的单调队列,[max(Si - Li, 0), Si - 1]中的决策依次加入候选集合,对于每个j = Si ~ N,先在队头检查决策合法性,然后
取队头为最优决策进行状态转移。
因为每个决策至多进队一次出队一次,故转移的时间复杂度可以均摊为O(1)。则整个算法的复杂度就是O(MN)
1 #include
2 #include
3 #include
4 #include
5 #include
6 #include
7 #include
8 #include
9 using namespace std;
10 const int maxn = 16010;
11 struct ddp {
12 int l, s, p;
13 }a[110];
14 int n, m, f[110][maxn], q[maxn];
15 inline bool cmp(ddp a, ddp b) {
16 return a.s < b.s;}
17 inline int read() {
18 int x = 0, y = 1;
19 char ch = getchar();
20 while(!isdigit(ch)) {
21 if(ch == '-') y = -1;
22 ch = getchar();
23 }
24 while(isdigit(ch)) {
25 x = (x << 1) + (x << 3) + ch - '0';
26 ch = getchar();
27 }
28 return x * y;
29 }
30 inline int ask(int i, int k) {
31 return f[i - 1][k] - a[i].p * k;
32 }
33 int main() {
34 n = read(), m = read();
35 for(int i = 1; i <= m; ++i)
36 a[i].l = read(), a[i].p = read(), a[i].s = read();
37 sort(a + 1, a + m + 1, cmp);
38 for(int i = 1; i <= m; ++i) {
39 int l = 1, r = 0;
40 for(int k = max(0, a[i].s - a[i].l); k <= a[i].s - 1; ++k) {
41 while(l <= r && ask(i, q[r]) <= ask(i, k)) r--;
42 q[++r] = k;
43 }
44 for(int j = 1; j <= n; ++j) {
45 f[i][j] = max(f[i][j - 1], f[i - 1][j]);
46 if(j >= a[i].s) {
47 while(l <= r && q[l] < j - a[i].l) l++;
48 if(l <= r) f[i][j] = max(f[i][j], ask(i, q[l]) + a[i].p * j);
49 }
50 }
51 }
52 cout << f[m][n] <<'\n';
53 return 0;
54 }
Cut the Sequence poj3017
给定一个长度为N的序列A,要求把序列分成若干段,在满足“每段中所有数的和”不超过M的前提下,让“每段中所有数的最大值”之和最小。试计算这个最小值。N <= 10^5,数列A中的数非负
且不超过10^6,M<=10^11
首先问题的理解一个重点在于,若干段!也就是说你根本不可能知道最多能几段
这样我们就需要枚举到第i个数时,之前的所有的段!(我可能是个傻,这么显然的我想了一天才想通
设f[i]表示在把前i个数分成若干段时把前i个数分成若干段,在满足每段中所有数的和不超过m时,每段的最大值的和的最小值。
这样我们可以想到这样的DP方程
i
f[i] = min{f[j] + max{Ak}(j+1<=k<=i)}(0 <= j < i && ΣAk <= M)
k=j+1
然后我们可以显然的发现数据范围N<=10^5,那么我们这个不加任何优化的dp肯定就炸了,于是我们要想想优化
若我们采用枚举决策j,然后从后向前枚举,这样我就需要O(n^2)的复杂度,依旧会超
然而该方程似乎很难被优化,因为max{Ak}不是用一个简单的多项式来表示,不容易找到单调性,这样我们不得不转移目标。
DP转移优化的指导思想是及时排除不可能的决策,保持候选集合的高度有效性和秩序性。
本着这样的原则,我们考虑j何时是必要的,
根据上述方程,若Aj为最优决策,除了Ak的累加和<=M外,还需要满足如下条件
1.Aj = max{Ak}
i i
2.ΣAk > M(即j是满足ΣAk <= M的最小的j)
k=j k=j+1
也就是说,假如某个位置j是最优决策,首先他必须是j<=k<=i的范围内的最大值,其次,它要是满足j+1<=k<=i的范围的累加和小于等于M的最小值
否则这个位置就不是最优决策,因为首先你不是这个范围的最大值,那么我肯定进行转移时不会用到你,其次,你这里也不是满足j+1<=k<=i的范围的累加和小于等于M的最小值,那我在你前面
就能找到满足这个条件的,那我要这个j就没有用处了
对于情况二,是比较好处理的,我们可以预处理出对于每一个i,满足条件二的最小j,记为c[i],在计算f[i]是,从c[i]进行一次转移即可,然后我们单独讨论处理第一个条件的j的维护方法
根据我们的分析,当我们要把一个新的决策j2插入候选集合中时,假如集合中已有决策j1,那么如果满足j1
Aj1也没有Aj2的值大。这样我们可以维护一个决策点j单调递增,并且Aj单调递减的队列,这有该队列中的元素有可能成为最优决策。
然而我们能发现的是,该队列是一个只有Aj单调递减的队列,但是对于方程f[j] + max{Ak}并没有单调性,我们不能直接取队头作为最优决策,因此我们需要加入一个能够维护值集合f[j]+max{Ak}
的数据结构,这样我们可以想到二叉堆,二叉堆与优先队列保持相同的候选集合,该插入时一起插入,该删除时一起删除。二叉堆以f[j] + max{Ak}作为比较大小的依据,快速在候选集合中查询最值
最后关于max{Ak}的计算,我们可以使用ST表预处理,O(1)查询,或者我们可以发掘单调队列的性质,队列中某一项的max{Ak}时间实际就是下一个元素的A值。
整个算法,每个j至多在单调队列和二叉堆中插入和删除1次,时间复杂度为O(NlogN)
//代码....等我艰难的写完再发...现已加入暑期豪华做题套餐
单调队列优化多重背包
多重背包
给定n种物品,其中第i中物品的体积为vi,价值为wi,并且有ci个。有一个容积为m的背包,要求选择若干个物品放入背包,使得物品的总体积不超过m的前提下,物品的价值总和最大
1.把第i中物品看做独立的ci个物品,进行0/1背包,O(N*M*Σci)的复杂度,如果我没算错...
2.进行二进制划分,使得每种物品能够达到O(logci)的复杂度
3.单调队列,可以说多重背包复杂度进一步优化到O(NM)
在多重背包解法中,DP数组忽略了“阶段”这一维。当外层循环进行到i时,f[j]表示从前i种物品中选出若干件放入背包,体积之和为j时,价值之和最大是多少。倒序循环j,在状态转移时,
考虑选取第i个物品的个数:cnt
f[j] = max{f[j - cnt * vi] + cnt * wi}(1 <= cnt <= ci)
画出能够转移到状态j的决策候选集合{j - cnt * vi | 1 <= cnt <= ci}
![]()
当循环变量j减小1时
![]()
可以发现,相邻两个状态j和j-1对应的决策候选集合没有重叠,很难快速地从j-1对应的集合得到j的集合
但是考虑状态j和j-vi,显然这两个会出现重复
这两者对应的决策候选集合之间的关系,与单调队列非常相似,只有一个新决策加入集合,同样也只有一个新决策离开集合
所以我们可以把状态j按照除以vi的余数分组,对每一组分别进行计算,不同组之间的状态j不会互相转移
余数为0: 0, vi, 2vi...
余数为1: 1, vi+1, 2vi+1...
......
余数为vi-1: (vi-1), (vi-1)+vi, (vi-1)+2vi...
把“倒序循环j”的过程,改为对每个余数u∈[0, vi - 1],倒序循环p = (M-u)/vi~0, 对应的状态就是j = u + p * vi。第i种物品只有ci个,故能转移到j = u + p * vi的决策候选集合
就是{u + k * vi | p - ci <= k <= p - 1}。新的状态转移方程就是:
f[u+p*vi] = max{f[u+k*vi] + (p - k) * wi}
与“Fence”类似,我们将i和u看做定值,当内层循环变量p减小1时,决策k的取值范围[p - ci, p - 1]的上下边界均单调减小。
对方程进行处理
f[u+p*vi] = max{f[u+k*vi] + p * wi - k * wi}
在进行内层循环k时,p可看做一个定值,这样方程可以变为
f[u+p*vi] = p*wi + max{f[u+k*vi] - k * vi}
这样方程式子等号右侧仍然分为两个部分:仅包含变量p和p*wi部分和仅包含变量k的f[u+k*vi] - k*wi。
然后对于f[u+p*vi],实际求得就是前f[u+k*vi]-k*vi的最大值,这样我们可以想到,每次求f[u+p*vi]时,实际是求得是一个存储f[u+k*vi]-k*vi的单调递减队列的队头元素,即最大值,
我们又知道,显然当k越大时,值是越大的,这样我们可以建立一个决策点k单调递减,数值f[u+k*vi] - k * wi单端递减的队列,用于维护候选集合,对于每个p,执行单调队列的三个惯例操作:
1.检查队头合法性,把大于p-1的决策点进队
2.取队头为最优决策,更新f[u+p*vi]
3.把新决策k=p-ci-1插入队尾,入队前检查队尾单调性,排除无用决策
总复杂度为O(NM)
1 #include
2 using namespace std;
3 const int maxn = 100086;
4 int n, m;
5 int f[maxn], v[maxn], w[maxn], c[maxn];
6 int q[maxn];
7 inline int read() {
8 int x = 0, y = 1;
9 char ch = getchar();
10 while(!isdigit(ch)) {
11 if(ch == '-') y = -1;
12 ch = getchar();
13 }
14 while(isdigit(ch)) {
15 x = (x << 1) + (x << 3) + ch - '0';
16 ch = getchar();
17 }
18 return x * y;
19 }
20 inline int calc(int i, int u, int k) {
21 return f[u + v[i] * k] - k * w[i];
22 }
23 int main() {
24 memset(f, 0x3f3f3f, sizeof(f));
25 n = read(), m = read();
26 f[0] = 0;
27 for(int i = 1; i <= n; ++i) {
28 v[i] = read(), w[i] = read(), c[i] = read();
29 for(int u = 0; u < v[i]; ++u) {
30 int l = 1, r = 0;
31 int maxp = (m - u) / v[i];
32 for(int k = maxp - 1; k >= max(maxp - c[i], 0); --k) {//插入最初的候选集合
33 while(l <= r && calc(i, u, q[r]) <= calc(i, u, k)) r--;
34 q[++r] = k;
35 }
36 for(int p = maxp; p >= 0; p--) {//倒序循环每个状态
37 while(l <= r && q[l] > p - 1) l++;//取队头进行状态转移
38 if(l <= r) f[u + p * v[i]] = max(f[u + p * v[i]], calc(i, u, q[l]) + p * w[i]);
39 if(p - c[i] - 1 >= 0) {//插入新决策,同时维护队尾单调性
40 while(l <= r && calc(i, u, q[r]) <= calc(i, u, p - c[i] - 1)) r--;
41 q[++r] = p - c[i] - 1;
42 }
43 }
44 }
45 }
46 int ans = 0;
47 for(int i = 1; i <= m; ++i)
48 ans = max(ans, f[i]);
49 cout << ans <<'\n';
50 return 0;
51 }
最后我们对单调队列优化DP的模型进行总结。
总结例题的状态转移方程
状态转移方程 定值(外层循环) 状态变量 决策变量
ans = max{s[i] - min{s[j]}(1-m<=j<=j-1)}(1<=i<=n) i i
f[i,j] = max{f[i-1,k] + pi*(j-k)} i j k
f[i] = min{f[j] + max{Ak}(j+1<=k<=i)}(0<=j
f[u+p*vi] = max{f[u+k*vi] + (p-k)*wi}(p-ci<=k<=p-1) i,u p k
ps:摘抄自《算法竞赛进阶指南》
只关注“状态变量”“决策变量”及其所在维度,这些状态转移方程都可以大致归为如下形式
f[i] = min{f[j] + val(i, j)}(L(i) <= j <= R(i))
上式所代表的的问题覆盖范围广泛,是DP中一类非常基本,非常重要的模型。这种模型也被称为1D/1D的动态规划。它是一个最优化问题,L(i)和R(i)是关于变量i的一次函数,限制了决策j的
取值范围,并保证其上下界变化具有单调性。val(i,j)是一个关于变量i和j的多项式函数,通常是决定我们采用何种优化策略的关键之处
回想三道例题解法,我们都把val(i,j)分成了两部分,第一部分仅与i有关,第二部分仅与j有关。对于每个i,无论采取哪个j作为最优决策,第一部分的值都是相等的,可以在选出最优决策更新
f[j]时再进行计算、累加。而当i发生变化时,第二部分的值不会发生变化,从而保证原来较优的决策,在i改变后仍然较优,不会产生乱序的现象。于是我们就可以在队列中维护第二部分的单调性,
及时排除不可能的决策,让DP算法第以高效进行。所以,在上述模型中,多项式val(i,j)的每一项仅与i和j中的一个有关,是使用单调队列进行优化的基本条件。
斜率优化
于是终于开始了斜率优化
对于DP经典模型f[i] = {f[j] + val(i, j)},在使用单调队列优化时一个基本条件:多项式val(i, j)的每一项仅与i和j中的一个有关。
那么对于多项式val(i, j)包含i和j的乘积项, 即存在一个同时与i和j有关的部分时,就需要使用斜率优化
tyvj1098任务安排
N个任务排成一个序列在一台机器上等待完成(顺序不得改变),这N个任务被分成若干批,每批包含相邻的若干任务。从时刻0开始,这些任务被分批加工
,第i个任务单独完成所需的时间是Ti。在每批任务开始前,机器需要启动时间S,而完成这批任务所需的时间是各个任务需要时间的总和(同一批任务将在
同一时刻完成)。每个任务的费用是它的完成时刻乘以一个费用系数Ci。请确定一个分组方案,使得总费用最小。
例如:S=1;T={1,3,4,2,1};F={3,2,3,3,4}。如果分组方案是{1,2}、{3}、{4,5},则完成时间分别为{5,5,10,14,14},费用C={15,10,30,42,56},总费用就是153。
1 <= N <= 5000, 1 <= S <= 50, 1 <= ti, ci <= 100
f[i]表示执行到第i个任务,但是我们知道题目要求是分批的,所以为了覆盖状态空间,我们在加一维
f[i, j]表示执行到第i个任务时,前i个任务分成了j批
这样在处理是我们就需要某个区间的时间和和费用系数和
于是很容易想到求两个前缀和数组sumT[i]和sumC[i]
思考转移:
方法一:显然的O(N^3)暴力
假设从第k + 1个任务开始到第i个任务结束作为第j批,对于第j批任务的完成时间就是j * S + sumT[i], 也就是说第j批任务的完成时刻是算上等待时间到处理完第i个任务的时间加上j批任务每次
启动机器的总时间,这样我们很容易写出DP方程
f[i, j] = max{f[k, j - 1] + (j * S + sumT[i]) * (sumC[i] - sum[k])}(0 <= k < i)
复杂度O(n^3)
方法二:
在上一个解法中,我们枚举了批数j,原因是为了确定机器启动了多少次,从而确定i在这一批任务完成的时刻
但是我们能够发现,机器因启动而花费的时间S,会累加到在此之后所有的任务的完成时刻,这就意味着我们不再需要枚举批数j
设f[i]表示把前i个任务分成若干批时的最小费用
f[i] = min{f[j] + sumT[i] * (sumC[i] - sumC[j]) + S * (sumC[N] - sumC[j])}(0 <= j < i)
1 #include
2 #define ll long long
3 using namespace std;
4 const int maxn = 5100;
5 int n, s, t, c;
6 ll f[maxn], sumc[maxn], sumt[maxn];
7 inline int read() {
8 int x = 0, y = 1;
9 char ch = getchar();
10 while(!isdigit(ch)) {
11 if(ch == '-') y = -1;
12 ch = getchar();
13 }
14 while(isdigit(ch)) {
15 x = (x << 1) + (x << 3) + ch - '0';
16 ch = getchar();
17 }
18 return x * y;
19 }
20 int main() {
21 n = read(), s = read();
22 for(int i = 1; i <= n; ++i) {
23 t = read(), c = read();
24 sumt[i] = sumt[i - 1] + t;
25 sumc[i] = sumc[i - 1] + c;
26 }
27 memset(f, 0x3f, sizeof(f));
28 f[0] = 0;
29 for(int i = 1; i <= n; ++i)
30 for(int j = 0; j < i; ++j)
31 f[i] = min(f[i], f[j] + sumt[i] * (sumc[i] - sumc[j]) + s * (sumc[n] - sumc[j]));
32 cout << f[n] <<'\n';
33 return 0;
34 }
接着我们把数据在扩大
扩大为: 1 <= N <= 3 * 10 ^ 5, 1 <= S, Ti, Ci <= 512
对上一题解法二进行优化,首先惯例对方程进行变形
f[i] = min{f[j] + sumt[i] *sumc[i] - sumt[i] * sumc[j] + S * sumc[n] - S * sumc[j]}
==> min{f[j] + sumt[i] * sumc[i] + S * sumc[n] - (sumt[i] + S) * sumc[j]}
去掉min函数,单独看大括号里的内容
f[j] + sumt[i] * sumc[i] + S * sumc[n] - (sumt[i] + S) * sumt[j]
仅把与j相关的值看做变量,其余的视作常量
得到f[j] = (S + sumt[i] * sumc[j]) + f[i] - sumt[i] * sumc[i] - S * sumc[n]
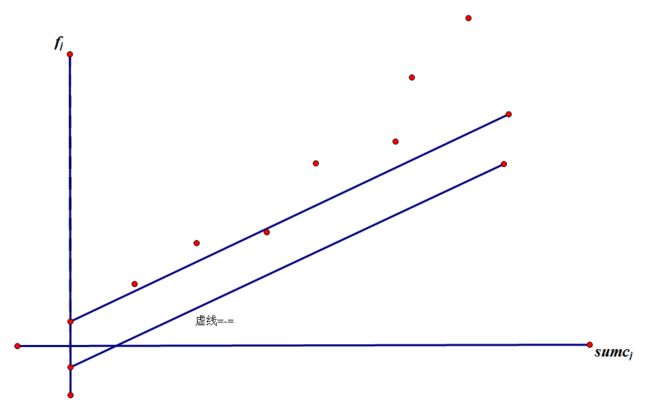
在sumc[j]为横坐标,f[j]为纵坐标的平面直角坐标系中,这是一条以S + sumt[i]为斜率,f[i] - sumt[i] * sumc[i] - S * sumc[n]为截距的直线。也就是说,决策候选集合是
坐标系中的一个点集, 每个决策j都对应着坐标系中的一个点(sumc[j], f[j])。每个待求解的状态f[i]都对应着一条直线的截距,直线的斜率是一个固定值S + sumc[i],截距未知,
但可以想象的是,当截距最小化时,f[i]就取到了最小值
然后我们可以知道的是,对于任何一个决策点(sumc[j], f[j])都可以解出一个截距,其中使截距最小的那个就是最优决策,所以这实际是一个线性DP,体现在坐标系中,就是用一条斜率
为固定正整数的直线自上而下平移,第一次解出某个决策点时,就得到了某个决策点的最小截距,如下图所示
对于任意三个决策点(sumc[j1], f[j1]), (sumc[j2], f[j2]), (sumc[j3], f[j3]),设j1
j2可能成为最优决策,根据“及时排除无用决策”的思想,考虑j2有可能成为最有决策的条件
已知j1 < j2 < j3那么我们想,首先,如果j2比j1更优
f[j1] - sumc[j1] > f[j2] - sumc[j2]
f[j2] - f[j1] > sumc[j2] - sumc[j1]
可得:(f[j2] - f[j1]) / (sumc[j2] - sumc[j1]) > 1
同理我们可以得到:
(f[j3] - f[j2]) / (sumc[j3] - sumc[j2]) > 1
事实上大于1没有半毛钱的关系,我拿来凑数的,我们看我们所得到的(f[j3] - f[j2]) / (sumc[j3] - sumc[j2]) 和 (f[j2] - f[j1]) / (sumc[j2] - sumc[j1])
f[j3] - f[j2]相当于点集(sumc[j2], f[j2]),(sumc[j3], f[j3])的纵坐标差,(sumc[j3] - sumc[j2])相当于横坐标差,也就是说(f[j3] - f[j2]) / (sumc[j3] - sumc[j2])
实际相当于当(sumc[j2], f[j2]),(sumc[j3], f[j3])在同一条直线上时,这条直线的斜率,我们设j2,j3构成直线的斜率为k2, j1,j2构成斜率的直线为k1
此时我们想:
k1 > 1是当j2比j1更优时得到的结论,同理上想,我们假设j2不是最优决策,那么对于j2和j3的关系,就有k2 < 1
此时k1 > k2,这样j2不是最优决策。即:
(f[j2] - f[j1]) / (sumc[j2] - sumc[j1]) > (f[j3] - f[j2]) / (sumc[j3] - sumc[j2])时
j2不是最优决策,在坐标系上表现为j1,j2连线,j2,j3连线,两条线段构成的形状上凸,也就是当连接j1,j2的线段与连接j2, j3的线段构成上凸形状时,无论直线的斜率为多少,都不可能
为最优
那么若j2是最优决策
有k1 > 1, k2 > 1,如何比较k1和k2的关系?
因为我们知道此时k1不可能 大于 k2
若 k1 == k2,此时三点共线,那么此时对于j2点的存在是没有意义的
对于j1, j2, j3点,因为三点在一条直线上,他们的决策是一样的,也就是说此时j2点的存在是无意义的,只需要j1和j3点就足够了
此时不是j2不可能为最优决策,而是“存在一种不用j2的最优决策”,j2也就失去了意义
于是此时,只有当k1 < k2时,j2点可能为最优决策。
j2是最优决策,在坐标系上表现为j1,j2连线,j2,j3连线,两条线段构成的形状下凸,也就是当连接j1,j2的线段与连接j2, j3的线段构成下凸形状时,j2可能为最优决策
对于本题也就是:
(f[j2] - f[j1]) / (sumc[j2] - sumc[j1]) < (f[j3] - f[j2]) / (sumc[j3] - sumc[j2])
如上所述,不等号两侧实际是连接两个决策点的线段的斜率,也就是我们应该维护的是 “连接相邻两点的线段斜率”单调递增的一个“下凸壳” ,只有这个“下凸壳”的顶点才有
可能成为最优决策。实际上,对于一条斜率为k的直线,若某个顶点在左侧线段的斜率比k小、右侧线段的斜率比k大, 则该顶点就是最优决策。那么如果把这条直线和所有线段组成一个
序列,那么令直线截距最小的顶点就出现在按照斜率大小排序时,直线应该排的位置上,如下图:
本题中,j的取值范围为0 <= j < i,随着i的增大,j的取值范围的上界每次增大1,即每次都有一个新决策进入候选集合。因为sumc[i]的单调性,所以每次出现的新决策的横坐标一定
大于之前所有决策,出现在凸壳的最右端。因为sumt的单调性,所以每次求出的直线斜率S + sumt[i]也单调递增,如果我们只保留凸壳上“连接相邻两点的线段斜率”大于S + simt[i]
的部分,那么凸壳最左端点的顶点一定是最优决策
综上所述,我们可以建立单调队列q,维护这个下凸壳。队列中保存若干个决策变量,对应凸壳上的顶点,且满足横坐标sumc递增、连接相邻两点的线段斜率也递增。
需要支持的操作:对于每个状态变量i
1.检查队头的两个决策变量q[l]和q[l+1],若斜率(f[q[l+1] - f[q[l]]]) / (sumc[q[l+1]] - sumc[q[l]]) <= s + sumt[i],这把q[l]出队,继续检查新的队头
2.直接取出队头j = q[l]为最优决策,执行状态转移,计算出f[i]
3.把新决策i从队尾插入,在插入前,若三个决策点j1 = q[r - 1], j2 = q[r], j3 = i不满足斜率单调递增(即不满足下凸性,即j2是无用决策),则直接从队尾将q[r]出队,继续检查新的队尾
因为每个决策入队一次出队一次,所以复杂度为O(n)
1 #include
2 using namespace std;
3 const int maxn = 100086;
4 int f[maxn], sumc[maxn], sumt[maxn];
5 int n, s;
6 int t, c;
7 int q[maxn], l = 1, r = 1;
8
9 inline int read() {
10 int x = 0, y = 1;
11 char ch = getchar();
12 while(!isdigit(ch)) {
13 if(ch == '-') y = -1;
14 ch = getchar();
15 }
16 while(isdigit(ch)) {
17 x = (x << 1) + (x << 3) + ch - '0';
18 ch = getchar();
19 }
20 return x * y;
21 }
22
23 int main() {
24 memset(f, 0x3f, sizeof(f));
25 n = read(), s = read();
26 for(int i = 1; i <= n; ++i) {
27 t = read(), c = read();
28 sumc[i] = sumc[i - 1] + c;
29 sumt[i] = sumt[i - 1] + t;
30 }
31 f[0] = 0;
32 q[1] = 0;
33 for(int i = 1; i <= n; ++i) {
34 while(l < r && (f[q[l + 1]] - f[q[l]]) <= (s + sumt[i]) * (sumc[q[l + 1]] - sumc[q[l]])) l++;
35 f[i] = f[q[l]] + sumt[i] * sumc[i] + s * sumc[n] - (sumt[i] + s) * sumc[q[l]];
36 while(l < r && (f[q[r]] - f[q[r - 1]]) * (sumc[i] - sumc[q[r]]) >= (f[i] - f[q[r]]) * (sumc[q[r]] - sumc[q[r - 1]])) r--;
37 q[++r] = i;
38 }
39 cout << f[n] <<'\n';
40 return 0;
41 }
与一般的单调优化DP的模型相比,本题维护“单调性”依赖于队列中相邻元素之间的某种“比值”。因为这个值对应着线性规划的坐标系中的斜率,所以把这种优化方法称为“斜率优化”。
英文称为convex hull trick,直译为“凸壳优化策略”
再扩大数据范围
1 <= n <= 3 * 10 ^ 5, 0 <= s, ci <= 512, -512 <= ti <= 512(bzoj2726)
也就是说此时出现了负数
这也就是说sumt不再具备单调性,也就是不能在单调队列中只保留凸壳上“连接相邻两点的线段的斜率”大于s+sumt[i]的部分,而是必须维护整个凸壳。这样一来,我们就不需要在队头把斜率与s + sumt比较
队头也不一定是最优决策,我们可以在单调队列中二分查找,求出一个位置p,p左侧线段的斜率比s + sumt[i]大,然后对队尾进行维护,维护方式和上一题相同
1 #include
2 using namespace std;
3 const int maxn = 100086;
4 int n, s;
5 int q[maxn], l = 1, r = 1;
6 int f[maxn], sumt[maxn], sumc[maxn];
7
8 inline int read() {
9 int x = 0, y = 1;
10 char ch = getchar();
11 while(!isdigit(ch)) {
12 if(ch == '-') y = -1;
13 ch = getchar();
14 }
15 while(isdigit(ch)) {
16 x = (x << 3) + (x << 1) + ch - '0';
17 ch = getchar();
18 }
19 return x * y;
20 }
21
22 inline int query_place(int i, int val) {
23 if(l == r) return q[l];
24 int L = l, R = r;
25 while(L < R) {
26 int mid = L + R >> 1;
27 if((f[q[mid + 1]] - f[q[mid]]) <= val * (sumc[q[mid + 1]] - sumc[q[mid]]))
28 L = mid + 1;
29 else R = mid;
30 }
31 return q[L];
32 }
33
34 int main() {
35 n = read(), s = read();
36 for(int i = 1; i <= n; ++i) {
37 int c, t;
38 t = read(), c = read();
39 sumt[i] = sumt[i - 1] + t;
40 sumc[i] = sumc[i - 1] + c;
41 }
42 q[1] = 0;
43 for(int i = 1; i <= n; ++i) {
44 int p = query_place(i, s + sumt[i]);
45 f[i] = f[p] + sumc[i] * sumt[i] + s * sumc[n] - (sumt[i] + s) * sumc[p];
46 while(l < r && (f[q[r]] - f[q[r - 1]]) * (sumc[i] - sumc[q[r]]) >= (f[i] - f[q[r]]) * (sumc[q[r]] - sumc[q[r - 1]]))
47 r--;
48 q[++r] = i;
49 }
50 cout << f[n] <<'\n';
51 return 0;
52 }
Cats Transport(Codeforces311B)
小S是农场主, 他养了M只猫, 雇了P位饲养员。农场中有一条笔直的路, 路边有N座山,从1到N的编号。第i座山与第i-1座山之间的距离为Di。饲养员都住在1号山
有一天,猫出去玩。第i只猫去Hi号山玩,玩到时刻Ti停止, 然后在原地等饲养员来接。饲养员们必须回收所有的猫。每个饲养员沿着路从1号山走到N号山,把各座山上的猫全部接走
饲养员在路上行走需要时间。饲养员在每座山上接猫的时间可以忽略,可以携带的猫的数量为无穷大。
例如有两座相距为1的山, 一只猫在2号山玩, 玩到时刻3开始等待。如果饲养员从1号山在2或3时刻出发,那么他可以接到猫,猫的等待时间0或1.而如果它与时刻1出发,那么他将于
时刻2到达第2号山, 不能接到此时仍在玩的猫
你的任务是规划每个饲养员从1号山出发的时间, 使得所有猫的等待时间的总和尽量小。饲养员出发的时间可以为负
数据范围:2 <= N <= 10 ^ 5, 1 <= M <= 10 ^ 5, 1 <= p <= 100
输入的第一行包含三个整数 N,M,P
第二行包含 n-1正整数d1, d2, d3,...dn
接下来m行每一行两个正整数hi和ti
M只猫,分别在hi号山上玩到ti,也就是说只有ti是才能去接第i只猫,第i座山与第i-1座山之间的距离为di
先预处理出距离前缀和数组S
对于每一只猫,设ai = ti - Σdj(1 <= j <= hi),也就是说,在ai之前出发的饲养员无法接到猫,则要想接到猫,饲养员必须在ai之后出发,若出发时间为t, 猫等待的时间就是t - ai
然后我们利用di的前缀和数组算出ai,将ai从小到大排序表示管理员出发时间先后从小到大排序。
我们的目的是让猫等待时间的总和尽量小。ai表示管理员的最早出发时间,根据贪心思想,我们设出发时间为ti的话,最终我们要求每一个ti-ai的总和尽可能的小
我们将ai从小到大排序后,最初的a1最小,若我们将a1放在后面处理,则显然t1 - a1会很大,而相应的,对于am,起始值就足够大,若先处理am,则在处理后面的情况时,则必须等到am
则后面的所有猫的等待时间会多出一个am来,这样显然不可能最优
因此我们想,若结果可能最优,则最初的ai要尽可能的小,所以处理猫的顺序要按照ai从小到大排排序后依次处理
得到这样的结论后,我们想显然我们管理员的数量不一定可以对应每一只猫,也就是说,处理问题的顺序必定是某一个管理员一次性带走排序后a序列中连续的若干只
当然这样就意味着我们需要求ai的前缀和数组
然后我们可以发现此题非常想任务安排
我们把管理员当做机器,处理的连续的一段猫当做要划分的批。
假设第i名管理员带走了第k + 1~j的猫, 那么管理员的最早出发时间就是aj,则猫的等待时间之和就是Σ(aj - ap)(k + 1 <= p <= j) = aj * (j - k) - (Sj - Sk)
于是我们设f[i, j]表示第i名管理员处理第k~1+j只猫是最小的时间总和
f[i, j] = min{f[i - 1, k] + Aj * (j - k) - (Sj - Sk)}(0 <= k < j)
这个式子我们需要O(PM^2)
按照常规思路,将外层循环i看做定值。
思考如何进行优化:
/*首先是对于要优化的内容,显然对于这个数据量,M和N巨大的范围使得我们根本无法使用O(n^2)或是O(n^3)的算法,然后我们并不需要快速查询当前位置之前的区间内已经处理过了的的
区间最值或是区间和,所以我们不需要也不能用数据结构优化*/
对方程进行分析后, 发现方程中存在乘积项Aj * k, 因此我们不能使用单纯的单调队列优化,于是很自然的就想到了使用斜率优化
将j看做状态变量,k是决策变量
先把方程去掉min.得到
f[i, j] = f[i - 1, k] + Aj * j - Aj * k - Sj + Sk
对方程进行移项,使得方程的两边只与一个变量有关,比如方程左边与只k有关,方程右边放j,k乘积项和只与j有关的项
f[i - 1, k] + Sk = f[i, j] - Aj * j - Aj * k + Sj
对决策思考优化:
将k看作横坐标,f[i - 1, k] + Sk看作纵坐标,此时直线斜率是Aj,当k = 0时,f[i - 1, k] + Sk == 0 && Aj * k == 0
则此时截距为f[i, j] - Aj * j + Sj,最终我们要取min值,则要求截距最小化
设三个决策点k1, k2, k3
若k2优于k1
f[i - 1, k2] + Sk2 + Aj * k2 < f[i - 1, k1] + Sk1 + Aj * k1
==>(f[i - 1, k2] + Sk2) - (f[i - 1, k1] + Sk1) < Aj * (k1 - k2)
==>(f[i - 1, k2] + Sk2) - (f[i - 1, k1] + Sk1) / (k2 - k1) < Aj
这样,我们要保证k1 < k2,而最优决策的集合中要维护斜率单调递增
我们要维护一个下凸壳。建立一个单调队列,队列中相邻两个决策k1, k2应满足k1 < k2并且斜率(f[i - 1, k2] + Sk2) - (f[i - 1, k1] + Sk1) / (k2 - k1)单调递增
因为斜率Aj从小到大排序过了, 所以在操作时,队列需要支持如下操作:
1.检查队头决策变量q[l]和q[l+1], 若斜率(f[i - 1, q[l+1]] + Sq[l+1]) - (f[i - 1, q[l]] + Sq[l]) / (q[l] - q[l+1]) <= Aj, 将队头出队,继续检查新的队头
2.取出队头k=q[l]为最优决策进行转移,计算出f[i, j]
3.把新的决策j插入队尾,插入前检查队尾q[r]和q[r-1]与j三点单调性,不满足斜率递增则出队,继续检查新的队尾
整个过程中每个决策进队一次出队一次,复杂度为O(m),外层枚举i,复杂度为O(p)
则总复杂度为O(PM)
1 #include
2 #define ll long long
3 using namespace std;
4 const int maxn = 1e5+10;
5 ll d[maxn], x, s[maxn], a[maxn];
6 int n, m, p;
7 ll f[4][maxn], ans = 1e18;
8 int q[maxn];
9
10 inline ll read() {
11 ll x = 0, y = 1;
12 char ch = getchar();
13 while(!isdigit(ch)) {
14 if(ch == '-') y = -1;
15 ch = getchar();
16 }
17 while(isdigit(ch)) {
18 x = (x << 1) + (x << 3) + ch - '0';
19 ch = getchar();
20 }
21 return x * y;
22 }
23
24 int main() {
25 n = read(), m = read(), p = read();
26 for(int i = 2; i <= n; ++i) {
27 d[i] = read();
28 d[i] += d[i - 1];
29 }
30 for(int i = 1; i <= m; ++i) {
31 x = read(), a[i] = read();
32 a[i] -= d[x];
33 }
34 sort(a + 1, a + m + 1);
35 for(int i = 1; i <= m; ++i)
36 s[i] = s[i - 1] + a[i];
37 fill(f[0] + 1, f[0] + m + 1, 1e18);
38 for(int i = 1; i <= p; ++i) {
39 int l = 1, r = 0;
40 q[++r] = 0;
41 for(int j = 1; j <= m; ++j) {
42 while(l < r && ((f[(i-1)%2][q[l+1]] + s[q[l+1]]) - (f[(i-1)%2][q[l]] + s[q[l]])) < a[j] * (q[l+1] - q[l]))
43 l++;
44 f[i%2][j] = f[(i-1)%2][q[l]] + a[j] * (j - q[l]) - s[j] + s[q[l]];
45 while(l < r && ((f[(i-1)%2][q[r]] + s[q[r]]) - (f[(i-1)%2][q[r-1]] + s[q[r-1]])) * (j - q[r]) > ((f[(i - 1)%2][j] + s[j]) - (f[(i-1)%2][q[r]] + s[q[r]])) * (q[r] - q[r-1]))
46 r--;
47 q[++r] = j;
48 }
49 ans = min(ans, f[i%2][m]);
50 }
51 cout << ans << '\n';
52 return 0;
53 }
最后补充一下写了4k题目的人民教育家lyd的斜率优化原理的解释
我可以去学学线性规划了=-=
四边形不等式
设w(x, y)是定义在整数集合上的二元函数、若对于定义域上任意整数a,b,c,d,其中a<=b<=c<=d,都有w(a, d)+w(b, c)>=w(a, c)+w(b, d)成立,则函数w满足四边形不等式
定理(四边形不等式的另一种定义)
设w(x, y)是定义在整数集合上的二元函数。若对于定义域上的任意整数a,b,其中a
证明,对于任意a
对于a+1 < c,有:w(a + 1, c + 1) + w(a + 2, c) >= w(a + 1, c) + w(a + 2, c + 1)
两式相加并移项得:w(a, c + 1) + w(a + 2, c) >= w(a, c) + w(a + 2, c + 1)
以此类推:对于a < b < c ,有:w(a, c + 1) + w(b, c) >= w(a, c) + w(b, c + 1)
则对于a < b < c < d ,有:w(a, d) + w(b, c) >= w(a, c) + w(b, d)
一维线性DP的四边形不等式优化
对于形如f[i] = min{f[j] + val(i, j)}的状态转移方程,记p[i]为令f[i]取到最小值的j的值,即p[i]为f[i]的最优决策。若p在[1, N]上单调不减(非严格单调递增),则称f具有决策单调性
定理(决策单调性)
在状态转移方程f[i] = min{f[j] + val(i, j)}中, 若函数val满足四边形不等式,则f具有单调性
证明:
∀i∈[1, N],∀j∈[0, p[i] - 1],根据p[j]的最优性,有:
f[p[i]] + val(p[i], i) <= f[j] + val(j, i)
∀i'∈[i + 1, N]因为val满足四边形不等式,有:
val(j, i') + val(p[i], i) >= val(j, i) + val(p[i], i')
移项得:
val(p[i], i') - val(p[i], i) <= val(j, i') - val(j, i)
与等式一相加有
f[p[i]] + val(p[i], i') <= f[j] + val(j, i')
这个不等式的含义为,以p[i]作为f[i']的决策,比以j < p[i]作为f[i']的决策更优。换言之,f[i']的最优决策不可能小于p[i],即p[i'] >= p[i]。所以f有决策单调性
//当f有决策单调性时,我们可以把f[i] = min{f[j] + val(j, i)}的计算时间从O(n^2)优化到O(nlogn)
考虑对p数组进行维护。最初p数组全部为0.在i循环进行的任意时刻,根据p[i]的单调性,p的情况如下图所示
求出一个新的f[i]时,我们应该考虑i可以作为哪些f[i'](i' > i)的最优决策。
根据决策单调性,最终我们会找到一个位置,在该位置之前,p数组目前存储的决策比i好,在该位置之后,p数组目前储存的决策比i差。因此我们需要快速找到这样的位置,然后把p数组该位置
之后的部分全部变为i
直接修改一个数组的效率低下。因此,我们可以建立一个队列,代替p数组
队列中保存若干个三元组(j, l, r),j表示决策,l, r表示目前p[l ~ r]的值都是j
例如第一幅图用5个三元组(j1, 1, 2),(j2, 3, 3),(j3, 4, 6),(j4, 7, 8),(j5, 9, 11)来表示。我们从队尾开始检查,判断出整个(j4, 7, 8),(j5, 9, 11)都不如i优,直接从队尾
删除,而(j3, 4, 6)左端比i优,右端比i差。因此我们在(j3, 4, 6)里二分查找,即可确定随求的位置。最后我们把(j3, 4, 6)变为(j3, 4, 5),把(i, 6, 11)入队,即可得到第二幅图所示
队列中没有必要保存小于p[1~i-1]的部分,我们可以通过检查队头来排除掉过时的决策。这样就可以像许多单调队列问题一样,直接取队头为最优决策即可
总而言之,对于每个i∈[1, N],我,们都将执行以下操作:
1.检查队头:设队头为(j0, r0, l0),若r0 = i-1,删除队头,否则令l0 = i
2.取队头保存的j为最优决策,执行转移,计算出f[i]
3.尝试插入新的决策:
(1)取出队尾,记为(jt, lt, rt)
(2)若对于f[lt]来说,i是比jt更优的决策,即:f[i] + val(i, lt) <= f[jt] + val(jt, lt)记pos = lt,插入队尾,回到步骤(1)
(3)若对于f[rt]来说,jt是比i更优的决策,即:f[jt] + val(jt, rt) <= f[i] + val(i, rt),执行步骤(5)
(4)否则,在[lt, rt]上二分查找,求出位置pos,在此之前决策jt更优,在此之后决策i更优,执行步骤(5)
(5)把三元组(i, pos, N)插入队尾
例题1:诗人小G(noi2009)
题目描述
小G是一个出色的诗人,经常作诗自娱自乐。但是,他一直被一件事情所困扰,那就是诗的排版问题。
一首诗包含了若干个句子,对于一些连续的短句,可以将它们用空格隔开并放在一行中,
注意一行中可以放的句子数目是没有限制的。
小G给每首诗定义了一个行标准长度(行的长度为一行中符号的总个数),他希望排版后每行的长度都和行标准长度相差不远。
显然排版时,不应改变原有的句子顺序,并且小G不允许把一个句子分在两行或者更多的行内。
在满足上面两个条件的情况下,小G对于排版中的每行定义了一个不协调度,
为这行的实际长度与行标准长度差值绝对值的P次方,
而一个排版的不协调度为所有行不协调度的总和。
小G最近又作了几首诗,现在请你对这首诗进行排版,使得排版后的诗尽量协调(即不协调度尽量小),并把排版的结果告诉他。
输入输出格式
输入格式:
输入文件中的第一行为一个整数T,表示诗的数量
接下来为T首诗,这里一首诗即为一组测试数据。每组测试数据中的第一行为三个由空格分隔的正整数N,L,P,其中:N表示这首诗句子的数目,L表示这首诗的行标准长度,P的含义见问题述。
从第二行开始,每行为一个句子,句子由英文字母、数字、标点符号等符号组成(ASCII码33~127,但不包含'-')。
输出格式:
于每组测试数据,若最小的不协调度不超过10^18,则第一行为一个数,表示不协调度。接下来若干行,表示你排版之后的诗。注意:在同一行的相邻两个句子之间需要用一个空格分开。
如果有多个可行解,它们的不协调度都是最小值,则输出任意一个解均可。若最小的不协调度超过10^18,则输出“Too hard to arrange”(不含引号)。每组测试数据结束后
输出“--------------------”(不含引号),共20个“-”,“-”的ASCII码为45,请勿输出多余的空行或者空格。
输入输出样例
输入样例#1: 复制
4
4 9 3
brysj,
hhrhl.
yqqlm,
gsycl.
4 9 2
brysj,
hhrhl.
yqqlm,
gsycl.
1 1005 6
poet
1 1004 6
poet
输出样例#1: 复制
108
brysj,
hhrhl.
yqqlm,
gsycl.
--------------------
32
brysj, hhrhl.
yqqlm, gsycl.
--------------------
Too hard to arrange
--------------------
1000000000000000000
poet
--------------------
说明
【样例说明】
前两组输入数据中每行的实际长度均为6,后两组输入数据每行的实际长度均为4。一个排版方案中每行相邻两个句子之间的空格也算在这行的长度中(可参见样例中第二组数据)
。每行末尾没有空格。
由样例可以发现的是,我们的排版处理是对整个句子进行的,因此我们可以首先设f[i]表示前i个句子排版后的最小不协调度
为了计算不协调对,我们需要知道的是每个句子的长度,设a[i]表示第i个句子的长度,事实上,对于每一行的诗,可能是不止一句诗的,我们要快速求取某一次排版情况下有若干句诗在同一行
时的不协调度,就需要这若干句诗的长度,这样我们就想到求出一个诗的长度的前缀和数组出来。sum[i]表示前i句诗的长度和
我们假设从第j+1到i的诗句排在一行,从样例中我们可以看到每行中相邻句子之间的空格也算在行长度中,因此我们需要再加上当j+1~i句作为一行时该行的空格数量
这样我们很容易能够得到dp方程
f[i] = min{f[j] + |(sum[i] - sum[j]) + (i - j - 1)| ^ p - L}(0 <= j < i)
这里val(j, i) = |(sum[i] - sum[j]) + (i - j - i)| ^ p,存在大量i, j的高次乘积项,不适合用单调队列或斜率优化。
于是我们尝试判断val(j, i)是否满足四边形不等式
证明对于任意j < i,val(j , i + 1) + val(j + 1, i) >= val(j, i) + val(j + 1, i + 1)
即证明:
val(j + 1, i) - val(j + 1, i + 1) >= val(j, i) - val(j, i + 1)
记:
u = (sum[i] + i) - (sum[j] + j) - (L + 1) // val(j, i) - L
v = (sum[i] + i) - (sum[j + 1] + j + 1) - (L + 1) // val(j + 1, i) - L
/*只需证明
|v|^p - |v + (a[i + 1] + 1)|^p >= |u|^p - |u + (a[i + 1] + 1)|^p
显然我们知道的是u > v(根据方程式子可以直接看出来)。
因此我们只需证明对任意常数c, 函数y = |x|^p - |x + c|^p单调递减*/
//恕我看不懂证明,只知道这个满足四边形不等式
综上所述=-=按照四边形不等式,用队列维护三元组即可
代码?算了吧写不动=-=应该还是有点没想通,暑假再写吧