一、heapq堆队列算法模块
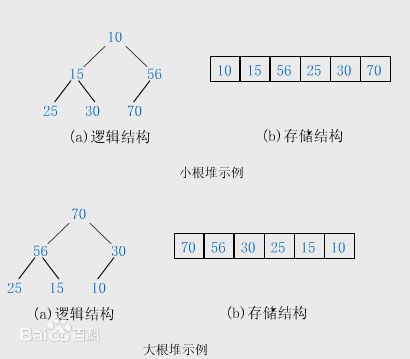
本模块实现了堆队列算法,也叫作优先级队列算法。堆队列是一棵二叉树,并且拥有这样特点,它的父节点的值小于等于任何它的子节点的值。
本模块实际上实现了一系列操作容器的方法,使之表现的如堆一般。
1、基本使用
heapq.heappush(heap, item)
把一项值压入list(用于表示堆heap),同时维持堆的排序要求。
import heapq
queue = []
heapq.heappush(queue, 5)
heapq.heappush(queue, 2)
heapq.heappush(queue, 1)
heapq.heappush(queue, 2)
queue
heapq.heappop(heap)
弹出并返回堆里最小值的项,调整堆排序。如果堆为空,抛出异常IndexError。
heapq.heappop(queue)
1
heapq.heapify(x)
就地转换一个列表为堆排序,时间为线性。
nums = [1, 8, 2, 23, 7, -4, 18, 23, 42, 37, 2]
heapq.heapify(nums)
nums
[-4, 2, 1, 23, 7, 2, 18, 23, 42, 37, 8]
初始化后仅仅保证前三个元素最小的顺序(最前端的树分支),在后面headpop会依次维护队列的输出最小:
for i in range(11):
print(heapq.heappop(nums))
-4 1 2 2 7 8 18 23 23 37 42
nums = [1, 8, 2, 23, 7, -4, 18, 23, 42, 37, 2]
for i in range(11):
print(heapq.heappop(nums))
1 2 -4 2 8 7 18 23 23 37 42
可见不初始化直接heapq.heappop前三个元素依然是最小的三个,但是不会被排序。
2、堆排序应用
问题
怎样从一个集合中获得最大或者最小的N个元素列表?
解决方案
heapq模块有两个函数:nlargest() 和 nsmallest() 可以完美解决这个问题。
import heapq
nums = [1, 8, 2, 23, 7, -4, 18, 23, 42, 37, 2]
print(heapq.nlargest(3, nums)) # Prints [42, 37, 23]
print(heapq.nsmallest(3, nums)) # Prints [-4, 1, 2]
和sorted类似,它们也接受关键字参数,
portfolio = [
{'name': 'IBM', 'shares': 100, 'price': 91.1},
{'name': 'AAPL', 'shares': 50, 'price': 543.22},
{'name': 'FB', 'shares': 200, 'price': 21.09},
{'name': 'HPQ', 'shares': 35, 'price': 31.75},
{'name': 'YHOO', 'shares': 45, 'price': 16.35},
{'name': 'ACME', 'shares': 75, 'price': 115.65}
]
cheap = heapq.nsmallest(3, portfolio, key=lambda s: s['price'])
expensive = heapq.nlargest(3, portfolio, key=lambda s: s['price'])
总结
- 当要查找的元素个数相对比较小的时候,函数nlargest() 和 nsmallest()是很合适的。
- 如果你仅仅想查找唯一的最小或最大(N=1)的元素的话,那么使用min()和max()函数会更快些。
- 类似的,如果N的大小和集合大小接近的时候,通常先排序这个集合然后再使用切片操作会更快点(sorted(items)[:N] 或者是 sorted(items)[-N:])。
- 需要在正确场合使用函数nlargest() 和 nsmallest()才能发挥它们的优势(如果N快接近集合大小了,那么使用排序操作会更好些)。
- 由于push和pop操作时间复杂度为O(N),其中N是堆的大小,因此就算是N很大的时候它们运行速度也依旧很快。
二、容器排序
python中两个容器比较大小,会从第0个元素开始比较,相等则下一位比较,不相等则返回,也就是说即使后面元素数目不一致或者不能比较大小也能够比较容器出大小。
class Item:
def __init__(self, name):
self.name = name
def __repr__(self):
return 'Item({!r})'.format(self.name)
a = Item('foo')
b = Item('bar')
a < b
# ---------------------------------------------------------------------------
# TypeError Traceback (most recent call last)
# in ()
# 1 a = Item('foo')
# 2 b = Item('bar')
# ----> 3 a < b
#
# TypeError: '<' not supported between instances of 'Item' and 'Item'
a = (1, Item('foo'))
b = (5, Item('bar'))
a < b
# True
甚至,
(1,2,3,4)>(0,1)
# True
三、优先级队列实践
import heapq
class PriorityQueue:
def __init__(self):
self._queue = []
self._index = 0
def push(self, item, priority):
heapq.heappush(self._queue, (-priority, self._index, item))
self._index += 1
def pop(self):
return heapq.heappop(self._queue)
class Item:
def __init__(self, name):
self.name = name
def __repr__(self):
return 'Item({!r})'.format(self.name)
>>> q = PriorityQueue()
>>> q.push(Item('foo'), 1)
>>> q.push(Item('bar'), 5) >>> q.push(Item('spam'), 4) >>> q.push(Item('grok'), 1) >>> q.pop() Item('bar') >>> q.pop() Item('spam') >>> q.pop() Item('foo') >>> q.pop() Item('grok') >>>
在上面代码中,队列包含了一个 (-priority, index, item) 的元组。优先级为负数的目的是使得元素按照优先级从高到低排序。这个跟普通的按优先级从低到高排序的堆排序恰巧相反。
index变量的作用是保证同等优先级元素的正确排序。通过保存一个不断增加的index下标变量,可以确保元素安装它们插入的顺序排序。而且,index变量也在相同优先级元素比较的时候起到重要作用。