网络流初步

以下内容均以此题为例讲解，以下贴的代码，都不能过，long long这些东西自己改，全部用int感觉美观一些

---

网络流

那么做这道模板题之前还是先了解一下网络流到底是个什么吧（因为我也是个初学者，如果有讲错或者不清楚的地方可以评论或者在其他dalao的题解或是博客中学习）

对于一个网络 \(G=(V,E)\) 是一个有向图，每一条边有一个边圈 \(c(x,y)\) 表示这条边的容量，你可以把它想象成一个下水道系统（？？？），每一条边都是一个管道，每个管道有自己允许流通的水的最大值。对于两个特殊节点， \(S\) 和 \(T\) （\(S\) ≠ \(T\)），如果有 \(S\in G\) 且 \(T\in G\)，称\(S\)为源点， \(T\) 为汇点，所有水从 \(S\) 流向 \(T\)

形如以下这个图：

那么 \(S->A->B->T\) 就是该网络的一个流，这个流的流量为2（该路径上的最小的容量）

那么对于这个流量，应该如何定义呢？我们引入一个流函数（摘自李煜东的《算法进阶》）

\(f(x,y)\)为定义在节点二元组（\(x\)∈\(V\),\(y\)∈\(V\)）上的实数函数，满足：

1. \(f(x,y)\) ≤ \(c(x,y)\)
2. \(f(x,y)\) ＝ \(-f(y,x)\)
3. \(\forall\) \(x\)≠\(S\)，\(x≠T\), \(\sum_{(u,x)∈E }f(u,x)=\sum_{(x,v)∈E }f(x,v)\)

\(f\)称为该网络的流函数，对于\((x,y)\)∈\(E\),\(f(x,y)\)为边的流量，\(c(x,y)-f(x,y)\)为该边的剩余容量

这三条性质分别为容量限制，斜对称和流量守恒。其中流量守恒告诉我们只有源点和汇点才会存储流，其流入总量等于流出总量

---

最大流

对于一个网络，有很多的流函数\(f\)都是合法的，那么使得整个网络的\(\sum_{(S,v)∈E }f(S,v)\)最大的流函数称为该网络的最大流，此时的流量为该网络的最大流量

那么求这个最大流，我会讲解 Edmonds-Karp增广路算法 和 Dinic算法，当然还有ISAP和HLLF等更加高效的算法，因为蒟蒻不太会，这里就不介绍，如果学会了会更新的

Edmonds-Karp增广路算法

时间复杂度：\(O(nm^2)\)

先介绍一下增广路是个什么：对于 \(S\) 到 \(T\) 的一条路径，如果路径上各边的剩余容量大于0，则这一条路径就是一条增广路

那么仔细一想，如果当前网络中还存在着那么一条增广路，那么说明我的流量还可以更大（见增广路的定义和剩余容量的定义），那么EK算法的核心思想就是不断地寻找增广路，直到无法找出最广路之后，说明找出了网络中的最大流

那么注意在实现寻找增广路时，我们可以用广搜实现，这样就可以保证找到每一条增广路

那么在找到增广路时，我们也应该去考虑反向边，用来反悔，也就是还原。在找到一条增广路时，路径上的容量应该减去这条增广路的流量，那么在处理这个东西之后就会影响到其它增广路，这个时候建反向边就可以起到一个反悔的作用

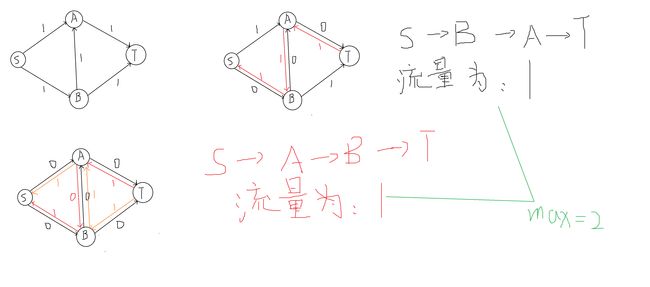
那么整个的模拟过程如下（从左往右看）：

那么我们就可以写出来第一份程序了

#include
using namespace std;
const int MAXN=50000;
const int INF=2147483649; //记得初始值写大点 
int n,m,s,t;
struct node{
	int net,to,w;
}e[MAXN];
int head[MAXN],tot=1;//注意这里是1，其实-1也行，看个人爱好 
void add(int x,int y,int z){
	e[++tot].net=head[x];
	e[tot].to=y;
	e[tot].w=z;
	head[x]=tot;
}
//领接表存边 
int ans;
int bian[MAXN],minn[MAXN]; //bian是用来记录路径的，minn表示增广路上各边的最小剩余容量 
bool v[MAXN];
bool bfs(){
	for(register int i=1;i<=n;i++) v[i]=false;
	queueq;
	q.push(s);
	v[s]=true;
	minn[s]=INF;
	while(!q.empty()){
		int x=q.front();
		q.pop();
		for(register int i=head[x];i;i=e[i].net){
			if(e[i].w!=0){ //不为0才走 
				int y=e[i].to,z=e[i].w;
				if(v[y]==true) continue; //增广路走过就不管了 
				minn[y]=min(minn[x],z);  
				bian[y]=i;
				v[y]=true;
				q.push(y);
				if(y==t) return true; //可以到达汇点 
			}
		}
	}
	return false;
}
void update(){
	int x=t;
	while(x!=s){
		int i=bian[x];
		e[i].w-=minn[t]; //正向边-
		e[i^1].w+=minn[t]; //反向边+ 
		x=e[i^1].to;
	}
	//这个异或1其实非常的秒
	//因为之前在存储边的时候，是直接正向反向一起存
	//所有反向边=正向边+1
	//一个偶数异或1=偶数+1
	//一个奇数异或1=奇数-1 
	ans+=minn[t]; //更新答案 
}
int main(){
	scanf("%d%d%d%d",&n,&m,&s,&t);
	for(register int i=1;i<=m;i++){
		int x,y,z;
		scanf("%d%d%d",&x,&y,&z);
		add(x,y,z); //有向边存储 
		add(y,x,0); //先存一个边权为0的反向边，有用 
	}
	while(bfs()==true) update(); //不断更新增广路 
	printf("%d",ans); //答案 
	return 0;
}

出题人毒瘤地卡掉了EK，但其实EK是能过的（想不到吧嘿嘿嘿），TLE的那两个点其实是因为有太多的重边，那么其实对于重边，我们只需要将重边累加，也可以AC的（@那一条变阻器，他用vector这么过的），其实在上面的程序的基础上改不了多少东西，就两行

#include 
using namespace std;
int n,m,s,t,u,v;
int w,ans,dis[520010];
int tot=1,vis[520010],pre[520010],head[520010],flag[2510][2510];

struct node {
	int to,net;
	int val;
} e[520010];

inline void add(int u,int v,int w) {
	e[++tot].to=v;
	e[tot].val=w;
	e[tot].net=head[u];
	head[u]=tot;
	e[++tot].to=u;
	e[tot].val=0;
	e[tot].net=head[v];
	head[v]=tot;
}

inline int bfs() {
	for(register int i=1;i<=n;i++) vis[i]=0;
	queue q;
	q.push(s);
	vis[s]=1;
	dis[s]=2005020600;
	while(!q.empty()) {
		int x=q.front();
		q.pop();
		for(register int i=head[x];i;i=e[i].net) {
			if(e[i].val==0) continue;
			int v=e[i].to;
			if(vis[v]==1) continue;
			dis[v]=min(dis[x],e[i].val);
			pre[v]=i;
			q.push(v);
			vis[v]=1;
			if(v==t) return 1;
		}
	}
	return 0;
}

inline void update() {
	int x=t;
	while(x!=s) {
		int v=pre[x];
		e[v].val-=dis[t];
		e[v^1].val+=dis[t];
		x=e[v^1].to;
	}
	ans+=dis[t];
}

int main() {
	scanf("%d%d%d%d",&n,&m,&s,&t);
	for(register int i=1;i<=m;i++) {
		scanf("%d%d%d",&u,&v,&w);
		if(flag[u][v]==0) {
			add(u,v,w);
			flag[u][v]=tot; //用一个数组记录这一条边 
		}
		else {
			e[flag[u][v]-1].val+=w; //累加重边 
		}
	}
	while(bfs()!=0) {
		update();
	}
	printf("%d",ans);
	return 0;
}

Dinic算法

时间复杂度： \(O(n^2m)\)

相对于之前EK算法来说，在稀疏图中的表现其实是差不多的，但是在稠密图中就快很多了，别妄想这总用第二个程序过，还是要学学一些更加优秀的算法（所以我为什么还不学ISAP之类的）

讲Dinic之前，我们不妨再引入一个东西：残量网络。任意时刻，在网络中所有节点以及剩余容量大于0的边构成的子图叫做残量网络。在EK算法中，每轮BFS会遍历整个残量网络，但只更新一条增广路，这就浪费了很多时间，就需要用Dinic算法了

我们设一个 \(d[x]\) 表示 \(x\) 的层次，如果满足\(d[y]=d[x]+1\) 的边\((x,y)\)，则它是一个分层图，是一个有向无环图

为什么用Dinic会更优呢，我们先用BFS求出每一个节点的深度，在分层图上DFS只去寻找到下一层的边，每一次找出多条增广路，这样就会快很多，但是BFS会跑很多遍，ISAP只用跑一遍，但是我不会（菜）

这其中还会涉及一个当前弧优化，听着很nb是吧，就是在更新第\(i\)条边时，前面\(i-1\)条边到汇点的流已经流蛮并且没有路可以走了，可以不去更新，我们记录一下就可以了，不需要重新去跑之前的边

至于实现的方法，直接在代码中讲解好了：

#include
using namespace std;
const int INF=2147483;
const int MAXN=50000;
int n,m,s,t;
struct node{
	int net,to;
	int w;
}e[MAXN];
int head[MAXN],tot;
void add(int x,int y,int z){
	e[++tot].net=head[x];
	e[tot].to=y;
	e[tot].w=z;
	head[x]=tot;
}
int de[MAXN]; //存储每一个点的层次 
int now[MAXN];//这个now可以暂时看为head的一个副本，所有值都一样 

bool bfs(){
	queueq;
	for(register int i=1;i<=n;i++) de[i]=INF;
	q.push(s);
	de[s]=0;
	now[s]=head[s]; //充分发挥一个作为副本的作用 
	while(!q.empty()){
		int x=q.front();
		q.pop();
		for(register int i=head[x];i;i=e[i].net){
			int y=e[i].to,z=e[i].w;
			if(z!=0&&de[y]==INF){ //如果当前边可以走且还没找过 
				q.push(y);
				now[y]=head[y];
				de[y]=de[x]+1; //更新层次 
				if(y==t) return true;
			}
		}
	}
	return false;
	//其实和EK的BFS差不了多少的 
}

int dfs(int x,int liu){ 
	if(x==t) return liu; //直接返回 
	int k,ans=0; //k是当前最小的剩余容量，
	for(register int i=now[x];i&&liu;i=e[i].net){
		now[x]=i;//当前弧优化 
		int y=e[i].to;
		if(e[i].w!=0&&(de[y]==de[x]+1)){
			k=dfs(y,min(liu,e[i].w)); //比较出一条更小的 
			if(!k) de[y]=INF;   //剪枝，去掉增广后的点 
			e[i].w-=k;
			e[i^1].w+=k; //正向反向更新 
			ans+=k; //流出去的流量和 
			liu-=k; //剩余流量减少 
		}
	}
	return ans;
}
int main(){
	scanf("%d%d%d%d",&m,&n,&s,&t);
	tot=1;
	for(register int i=1;i<=m;i++){
		int x,y,z;
		scanf("%d%d%d",&x,&y,&z);
		add(x,y,z);
		add(y,x,0);
	}
	int maxx=0; //最大流 
	while(bfs()) maxx+=dfs(s,INF);//记录答案 
	printf("%d",maxx);
	return 0;
}

感谢一下@那一条变阻器和@取什么名字 两个大佬的指点，当然还有其他题解（因为我最开始自己也不会编啊~~~）