cs224笔记：Lecture 6 Language Models and RNNs

Language Models and RNNs

1 Language Model

Language Model is the task of predicting what word comes next.
更正式的：给定一个单词序列，${\mathbf{x}}^{(1)},{\mathbf{x}}^{(2)},...,{\mathbf{x}}^{(t)}$，预测下一个单词${\mathbf{x}}^{(t+1)}$的概率分布。
$$p({\mathbf{x}}^{(t+1)}|{\mathbf{x}}^{(1)},{\mathbf{x}}^{(2)},...,{\mathbf{x}}^{(t)})$$
${\mathbf{x}}^{(t+1)}$可以是单词表$V=\{w_1,...,w_{|V|}\}$中的任意单词。这样的系统成为language model，也可以理解为给一段文本分配概率。
$$\begin{gathered} p({\mathbf{x}}^{(1)},{\mathbf{x}}^{(2)},...,{\mathbf{x}}^{(t)})=p({\mathbf{x}}^{(1)})\times p({\mathbf{x}}^{(2)}|{\mathbf{x}}^{(1)})\times \cdots \times p({\mathbf{x}}^{(T)}|{\mathbf{x}}^{(T-1)},{\mathbf{x}}^{(T-2)},...,{\mathbf{x}}^{(1)}) \\ =\prod _{t=1}^{T}p({\mathbf{x}}^{(t)}|{\mathbf{x}}^{(t-1)},...,{\mathbf{x}}^{(1)}) \end{gathered}$$

Language Model是一个benchmark task，可以帮助我们评估对语言的理解的程度。
同时，Language Model是许多NLP任务的组成部分(subcomponent)，尤其是对于那些包含文本生成(generating text)和估计给定文本概率(estimating the probability of text)的任务。
• Predictive typing
• Speech recognition
• Handwriting recognition
• Spelling/grammar correction
• Authorship identification
• Machine translation
• Summarization
• Dialogue
• etc.

2 n-gram Language Models

n-gram 就是n个连续的单词，根据n的不同，有不同的类型，比如对于同一句话 the students opened their __ 有：
unigram: “the” “students” “opened” “their”
bigram：“the students” “students opened” “opened their”
trigram: “the students opened” “students opened their”
4-gram: “the students opened their”
可以看出n越大涵盖的信息多，模型相较就会更精准一些。

n-gram language model的思想就是统计不同n-gram出现的频率，用于预测单词。(其实就是简单的counts)
首先，n-gram language model的简单假设就是一个单词${\mathbf{x}}^{(\mathbf{t})}$只依赖于它前面的n-1个单词，即：
$$p({\mathbf{x}}^{(t+1)}|{\mathbf{x}}^{(t)},{\mathbf{x}}^{(t-1)},...,{\mathbf{x}}^{(1)})=p({\mathbf{x}}^{(t+1)}|{\mathbf{x}}^{(t)},{\mathbf{x}}^{(t-1)},...,{\mathbf{x}}^{(t-n+2)})$$
然后根据条件概率定义计算它，
$$p({\mathbf{x}}^{(t+1)}|{\mathbf{x}}^{(t)},{\mathbf{x}}^{(t-1)},...,{\mathbf{x}}^{(t-n+2)})=\frac{p({\mathbf{x}}^{(t+1)},{\mathbf{x}}^{(t)},...,{\mathbf{x}}^{(t-n+2)})}{p({\mathbf{x}}^{(t)},...,{\mathbf{x}}^{(t-n+2)}))}$$
分子是n-gram出现的概率，分母是(n-1)-gram出现的概率，通过对大规模语料库的统计，可以获得这两个概率的近似(statistical approximation)，即：
$$\frac{p({\mathbf{x}}^{(t+1)},{\mathbf{x}}^{(t)},...,{\mathbf{x}}^{(t-n+2)})}{p({\mathbf{x}}^{(t)},...,{\mathbf{x}}^{(t-n+2)}))}\approx \frac{count(x^{(t+1)},x^{(t)},...,x^{(t-n+2)})}{count(x^{(t)},...,x^{(t-n+2)})}$$
e.g. 学习一个4-gram language model，句子为：
$$\text{as the proctor started the clock, the students opened their \_\_ }$$

$$p(w|\text{ students opened their })=\frac{count(\text{ students opened their w })}{count(\text{ students opened their })}$$

假设在语料库中，"students opened their"出现了1000次，"students opened their books"出线了400次，"students opened their exams"出线了100次，则
$$\begin{gathered} p(\text{books}|\text{ students opened their })=\frac{count(\text{ students opened their books })}{count(\text{ students opened their })}=0.4 \\ p(\text{exams}|\text{ students opened their })=\frac{count(\text{ students opened their examss })}{count(\text{ students opened their })}=0.1 \end{gathered}$$

N-gram language model的问题

Sparsity Problem(稀疏问题)

$$p(w|\text{ students opened their })=\frac{count(\text{ students opened their w })}{count(\text{ students opened their })}$$

首先是分子的问题，“students opened their w”有可能没在语料库出现过，所以这个概率为0。
解决：给每个单词$w\in V$都加上一个很小的值$\delta$，这个方法称为smoothing。

然后是分母的问题，“students opened their”有可能没出现过，这样对于任何概率都无法计算。
解决：backoff(回退)，统计"opened their"作为替代。

Storage Problem(存储问题)

对于每一个出现过的n-gram都需要存储下来，随着n的增大，要存储的规模也会增大。

所以引出了一个矛盾，我们希望大一点n使得模型更加精确，但是n越大会引发sparsity problem和storage problem。

3 Neural Language Models

a fixed-window language model

$$\text{as the proctor started the clock, the students opened their \_\_}$$

还是同样的例子，假设window大小为4，则我们的模型只用到"the students opened their"来预测下一个单词。

其中输入${\mathbf{x}}^{(1)},{\mathbf{x}}^{(2)},{\mathbf{x}}^{(3)},{\mathbf{x}}^{(4)}$为one-hot编码的向量，接着将词嵌入(word embedding)后的词向量拼接(concatenation)成一个向量$\mathbf{e}=[{\mathbf{e}}^{(1)};{\mathbf{e}}^{(2)};{\mathbf{e}}^{(3)};{\mathbf{e}}^{(4)}]$，然后经过一个隐层，$\mathbf{h}=f(\mathbf{W}\mathbf{e}+{\mathbf{b}}_1)$，最后softmax输出获得概率分布，$\hat{\mathbf{y}}=softmax(\mathbf{U}\mathbf{h}+{\mathbf{b}}_2)\in {\mathbb{R}}^{|V|}$

相较n-gram模型的改进：

没有sparsity问题；
不需要存储观测到的所有n-gram。

存在的问题：

固定窗口(fixed window)不够大，扩大窗口就相当于扩大$\mathbf{W}$，因而窗口不能太大；
因为各个单词通过拼接组成的$\mathbf{e}$，使得不同的单词对应$\mathbf{W}$矩阵不同的位置，这样相当于丢失了机器学习很重要的特性–共享权重。例如：
$$\mathbf{W}\mathbf{e}=[{\mathbf{w}}_1,{\mathbf{w}}_2,{\mathbf{w}}_3,{\mathbf{w}}_4]\left[\begin{array}{c}{\mathbf{e}}_1\\ {\mathbf{e}}_2\\ {\mathbf{e}}_3\\ {\mathbf{e}}_4\end{array}\right]$$
可以看出$\mathbf{W}$中不同块对应不同的单词，即丢失了对称性(symmetry)。

4 RNN Language Models

4.1 RNN(Recurrent Neural Network)

Core idea: 重复的运用同一个权重$\mathbf{W}$。可以同上面fixed window neural做比较，RNN中$\mathbf{W}$会重复用在输入序列每个词上面。

4.2 a RNN Language Model

如图，输入为one-hot编码的词向量${\mathbf{x}}^{(t)}$，首先词嵌入(word embedding)成稠密向量${\mathbf{e}}^{(t)}=\mathbf{E}{\mathbf{x}}^{(t)}$，接着隐层计算，每个隐层的输入${\mathbf{h}}^{(t)}$包括${\mathbf{x}}^{(t)}$和上一时刻的隐层${\mathbf{h}}^{(t-1)}$，${\mathbf{h}}^{(t)}=\sigma ({\mathbf{W}}_{\mathbf{h}}{\mathbf{h}}^{(t-1)}+{\mathbf{W}}_{\mathbf{e}}{\mathbf{e}}^{(t)}+{\mathbf{b}}_1)$，最后输入通过softmax获取概率分布，${\hat{\mathbf{y}}}^{(t)}=softmax(\mathbf{U}{\mathbf{h}}^{(t)}+{\mathbf{b}}_2)\in {\mathbb{R}}^{|V|}$。这里任意时刻都可以获得输出，取决于你想让模型做什么样的预测。此外输入序列可以任意长度。

RNN优点：

可以处理任意长度的序列；
在时刻t的计算，可以获取到很多步前的输入信息；
模型规模不会随着输入序列增大而增大；
权重$\mathbf{W}$应用到每个时刻的输入上，所以对于任意的输入，权重$\mathbf{W}$有对称性(symmetry)。

RNN缺点:

循环计算(recurrent computation)很慢；
很难获取到很多步前的信息；

4.3 训练RNN Language Model

给定一个文本的语料库(corpus)，由单词序列组成${\mathbf{x}}^{(1)},{\mathbf{x}}^{(2)},...,{\mathbf{x}}^{(T)}$。对于RNN-LM，在每一步t，计算输出概率分布${\hat{\mathbf{y}}}^{(t)}$，即根据之前的所有单词，预测下个单词。

每一步t的损失函数定义为预测概率分布${\hat{\mathbf{y}}}^{(t)}$与真实的下个个单词${\mathbf{y}}^{(t)}$(${\mathbf{x}}^{(t+1)}$的one-hot)之间的互熵损失(cross entropy):
$$J^{(t)}(\theta )=CE({\mathbf{y}}^{(t)},{\hat{\mathbf{y}}}^{(t)})=-\sum _{w\in \mathbf{V}}{\mathbf{y}}_w^{(t)}\log {\hat{\mathbf{y}}}_w^{(t)}=-\log {\hat{\mathbf{y}}}_{{\mathbf{x}}_{t+1}}^{(t)}$$
总的损失(overall loss)为整个训练集loss的均值：
$$J(\theta )=\frac{1}{T}\sum _{t=1}^T{J}^{(t)}(\theta )=\frac{1}{T}\sum _{t=1}^T-\log {\hat{\mathbf{y}}}_{{\mathbf{x}}_{t+1}}^{(t)}$$
但是在整个语料库上计算损失(loss)和梯度(gradient) too expensive，实践中在一个句子上或者一个文本上做计算。

4.4 Backpropagation for RNNs

Multivariable Chain Rule

给定一个多变量(multivariable)函数$f(x,y)$，其中$x(t)$和$y(t)$是单变量(single variable)函数，下面是multivariable chain rule：
$$\frac{d}{d_t}f\left(x(t),y(t)\right)=\frac{\partial f}{\partial x}\frac{dx}{dt}+\frac{\partial f}{\partial y}\frac{dy}{dt}$$

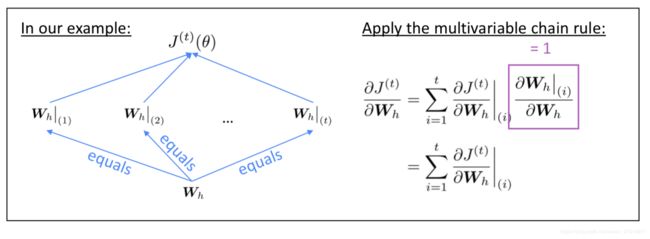
所有对于RNN权重$\mathbf{W}$的梯度计算如图，也就是运用multivariable chain rule将每个时刻对权重$\mathbf{W}$的梯度加起来：

关于$\frac{\partial J^{(t)}}{\partial {\mathbf{W}}_h}={\sum }_{t=1}^t\frac{\partial J^{(t)}}{\partial {\mathbf{W}}_h}{|}_i$的计算为按照时间$i=t,...,0$反向传播，将梯度加起来，算法被称为backpropagation through time(BPTT)。

评估Language Model

对于language model一个标准的评估度量是perplexity (perplexity越小越好)
$$perplexity=\prod _{t=1}^T{\left(\frac{1}{P_{LM}({\mathbf{x}}^{(t+1)}|{\mathbf{x}}^{(t)},...,{\mathbf{x}}^{(1)})}\right)}^{1/T}$$
等价于互熵损失的指数：
$$\begin{array}{rl}& =\prod _{t=1}^T{\left(\frac{1}{{\hat{\mathbf{y}}}_{{\mathbf{x}}_{t+1}}^{(t)}}\right)}^{1/T}\\ & =exp(\frac{1}{T}\sum _{t=1}^T-\log {\hat{\mathbf{y}}}_{{\mathbf{x}}_{t+1}}^{(t)})\\ & =exp(J(\theta ))\end{array}$$