时间序列的R语言实现

时间序列简介

时间序列（或称动态数列）是指将同一统计指标的数值按其发生的时间先后顺序排列而成的数列。时间序列分析的主要目的是根据已有的历史数据对未来进行预测。

本文主要记录时间序列的几种模型及其R语言实现。

需要用到的包：

library(zoo)
library(forecast)
library(tseries)

白噪声的判断

首先，我们先对数据进行检测，判断数据是否是白噪声（纯随机序列）

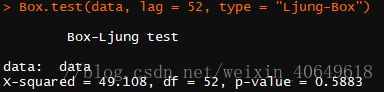
这里可以使用Box-Ljung 检验

Box.test(data, lag = 52, type = "Ljung-Box")

这里的P值显然大于0.05，不能拒绝原假设，故数据序列为白噪声，时间序列模型不适合本数据序列。

若通过Box-Ljung 检验，则说明时间序列模型可以用来对数据进行预测。接下来将介绍几种经典的时间序列模型。

1.ARMA模型

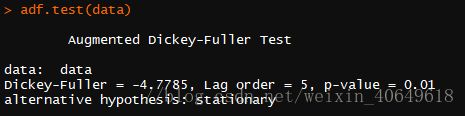
ARMA也叫自回归移动平均混合模型。ARMA模型经常在时间序列中使用。在ARMA模型中，AR代表自回归，MA代表移动平均。他们均是用于平稳序列，因此在使用ARMA模型之前必须进行平稳性检验。（需要用到tseries包）

adf.test(data)

p = 0.01<0.05，故拒绝原假设，数据是平稳的。

若p>0.05，则需要对原数据进行一阶差分

datadiff1 <- diff(data, differences = 1)

之后再进行平稳性检验，直至数据平稳。

平稳后，进行ARIMA参数的确定。

自动确定参数：可以使用autoarima函数，它会返回ARIMA的各个参数，不过autoarima进行参数的选择时它只注重AIC值的大小，所得出的结果并不一定时最好的，这个方法并不是特别推荐。

人工选择参数：画出acf图得出arima（p,d,q)中p,q参数的值。而d为差分次数。

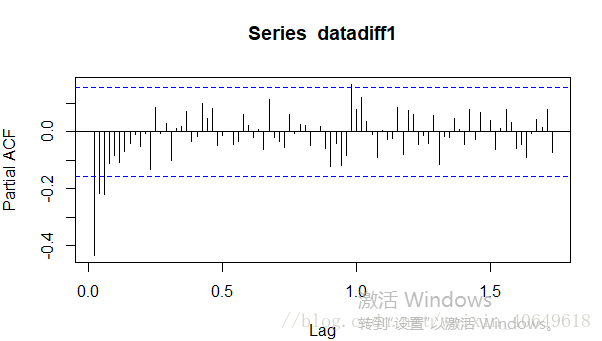
acf(datadiff1, lag.max = 90)
pacf(datadiff1, lag.max = 90)

这两个图判断自相关系数和偏自相关系数是拖尾还是截尾。acf图对应的是q的值，pacf图对应的是p的值，若是拖尾，则值为0，若是截尾，则看是几期截尾得出对应参数的值。图中可读出p=3,q=2。接着建立模型。

datamodel <- arima(data, order = c(3,1,2), seasonal = list(order=c(1,1,1)))

其中seasonal是季节性参数。三个参数分别为P,D,Q，根据其周期以及几部差分来判断其值。

建立完模型需要进行AIC值检验，其值越小越好。

AIC(datamodel)

dataforcast <- forecast(datamodel, h = 7)
dataforcast
plot(dataforcast)

输出模型预测后的七个值。

2.Holt-winters模型

Holt-winters模型中有三个参数，gamma是 季节改变平滑因子，beta是数据平滑因子，alpha是趋势平滑因子

dataseries <- ts(data, start = c(2015,1), frequency = 52)
plot(dataseries)
dataseriesHW <- HoltWinters(dataseries, gamma = T, beta = F, alpha = 0.2)
plot(dataseriesHW)
dataforcast <- forecast(dataseriesHW, h = 4)
dataforcast
plot(dataforcast)