数据结构与算法---遍历二叉树
二叉树
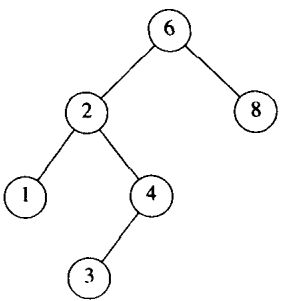
概念:父节点,左儿子、右儿子
6是根节点,同时6也是父节点,2是6的左儿子,8是6的右儿子。
遍历策略
前序遍历:根左右
中序遍历:左根右
后序遍历:左右根
三个一起对比记忆则很好记。
栈stack
为了遍历二叉树,我们把遍历的节点压入栈,打印一个则出栈。
Java中创建栈:
Stack stack = new Stack<>();
前序遍历
遍历策略:根左右
递归
public static void preOrderRecur(Node head) {
//前序遍历为根左右
if(head == null) {
return ;
}
System.out.print(head.value+" ");
preOrderRecur(head.left);
preOrderRecur(head.right);
}
非递归
因为前序遍历是自顶向下的,因此在沿顶一直向下打印即可
public void preOrderUnRecur(Node head) {
System.out.println("pre-order");
if(head!=null) {
//由于前序遍历是根左右,因此pop永远是在自述
Stack stack = new Stack(); //栈
stack.add(head); //返回压栈是否成功
while(!stack.isEmpty()) {
head = stack.pop();
System.out.println(head.value+" ");
if(head.right!=null) {
stack.push(head.right);
}
if(head.left != null) {
stack.push(head.left);
}
}
}
System.out.println();
}
中序遍历
递归
public static void inOrderRecur(Node head) {
//中序遍历为左根右
if (head==null){
return ;
}
inOrderRecur(head.left);
System.out.print(head.value+" ");
inOrderRecur(head.right);
}
非递归
左根右,因此沿左侧一直往下遍历,直到左节点为null时则返回父节点向右遍历。
public void inOrderUnRecur(Node head){
//首先判断head是否为空,是的话就没有必要遍历了
if(head != null) {
//head不为空,我们选用stack栈的数据结构来存储数据。
//中序遍历是左根右,意味着我们要首先找到最左边的数据,然后打印出来
Stack stack = new Stack();
while(!stack.isEmpty() || head!=null) {
if(head!=null) {
stack.push(head);
head = head.left;
}else { //遍历到左侧最底,没有数据的情况下,这个时候就顺势打印出最左边的数据。有一种情况是左侧没有数据,那么打印的就应该是中间节点。
head = stack.pop();
System.out.println(head.value+" ");
head = head.right;
}
}
}
}
后序遍历
递归
public static void posOrderRecur(Node head) {
//后序遍历为左右根
if (head==null){
return ;
}
posOrderRecur(head.left);
posOrderRecur(head.right);
System.out.print(head.value+" ");
}
非递归
由于后序遍历是左右根,因此是从底层往上打印节点。但一直向左侧遍历不能区分父节点和儿子节点,因此用一个辅助节点记住上次打印过的值。
public static void posOrderUnRecur(Node head) {
//从底层往上打印
//Node h = null;
if (head != null) {
//肯定要先遍历到最左侧,但遍历的终点可能是父节点或左儿子节点
//考虑到后序遍历是左右根,只有当目前节点的左右儿子节点 都为null时 才打印。
//要判断节点是左节点还是父节点
//还是要获取父节点
Stack stack = new Stack<>();
Node c = null;
stack.push(head);
Node h = head;
while(!stack.isEmpty()) {
c = stack.peek();
if(c.left!=null && h!=c.left &&h!=c.right) {//&& head.left!=null && head.right != null
stack.push(c.left);
}else if(c.right!=null && h!= c.right) {
stack.push(c.right);
}else {
System.out.println(stack.pop().value+" ");
h = c;
}
}
}
System.out.println();
}
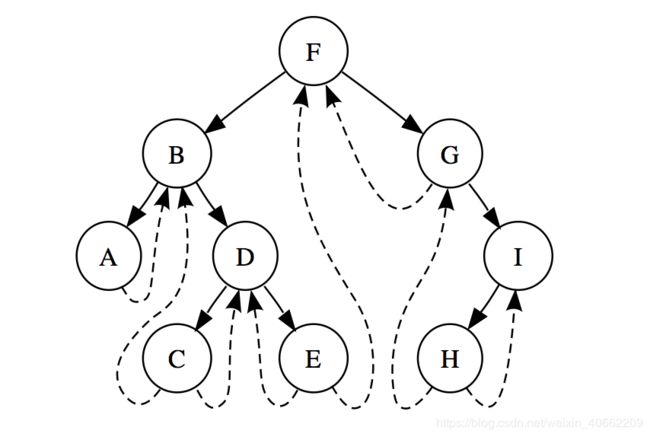
神级遍历方法—mirrors
无论是上面的递归还是非递归,都要用到函数栈,申请的栈空间与树的高度相关,所以平均空间复杂度为O(nlgn)。
morris遍历则保证了空间复杂度为O(1),时间复杂度也在O(n)。
public static void mirrors(Node head) {
// cur 为遍历节点
//1.mostright为cur节点的左子树的最右节点
//如果有左子树,找到mostright,如果mostright==0,mostright=cur,cur往左走;如果mostright==cur,cur往右走,mostright=null;
//如果没有左子树,cur就往右走。
if (head ==null) {
return ;
}
Node cur = head;
Node mostright = null;
while(cur!=null) {
mostright = cur.left;
if(mostright!=null) {
while(mostright.right!=null && mostright.right!=cur) {
mostright = mostright.right;
}
if(mostright.right==null) {
mostright.right = cur;
cur = cur.left;
continue;
}else {
mostright.right = null;
}
}
cur =cur.right;
}
}
规律:对于有左子树的节点都可以到达两次,对于没有左子树的节点都只到达一次。
利用这一点可以用来前序中序遍历。
前序遍历之Morris实现
根左右
- 对于cur可以到达两次的节点(有左子树的节点),cur第一次到达时打印,第二次到达时不打印。
- 对于cur只能到达一次的节点,cur到达时直接打印。
public static void morrisPre(Node head) {
//到达两次的节点,第一次到达就打印;
//到达一次的节点,直接打印
if(head == null) {
return ;
}
Node cur = head;
Node mostright = null;
while(cur!=null) {
mostright = cur.left;
if(mostright!=null) {
while(mostright.right != null && mostright.right !=cur) {
mostright = mostright.right;
}
if(mostright.right == null) {
System.out.print(cur.value+" ");
mostright.right = cur;
cur = cur.left;
continue;
}else {
mostright.right = null;
cur = cur.right;
continue;
}
}
System.out.print(cur.value+" ");
cur = cur.right;
}
System.out.println();
}
中序遍历之Morris实现
左根右
3. 对于cur到达一次的节点直接打印
4. 对于cur到达两次的节点,第二次打印,即mostright==cur的时候
public static void morrisIn(Node head) {
//到达两次的节点,第一次到达就打印;
//到达一次的节点,直接打印
if(head == null) {
return ;
}
Node cur = head;
Node mostright = null;
while(cur!=null) {
mostright = cur.left;
if(mostright!=null) {
while(mostright.right != null && mostright.right !=cur) {
mostright = mostright.right;
}
if(mostright.right == null) {
mostright.right = cur;
cur = cur.left;
continue;
}else {
mostright.right = null;
System.out.print(cur.value+" ");
cur = cur.right;
continue;
}
}
System.out.print(cur.value+" ");
cur = cur.right;
}
System.out.println();
}
后序遍历之Morris实现

G-F-D-E只到达过一次,B-C-A到达过两次
F-M-L-H-G-E-D-C-B-A
对于B而言,第一次到达B不打印,第二次到达B后,打印了F;
对于G而言,第一次到达G不打印,第二次到达G后,打印了M;
对于C而言,第一次到达C不打印,第二次到达C后,打印了L-H-G;
对于A而言,第一次到达A不打印,第二次到达A后,打印了E-D-C-B。
B G C A是第二次到达的顺序,因此,cur到达第二次时,就逆序打印左子树的右边界(包括其左子树)
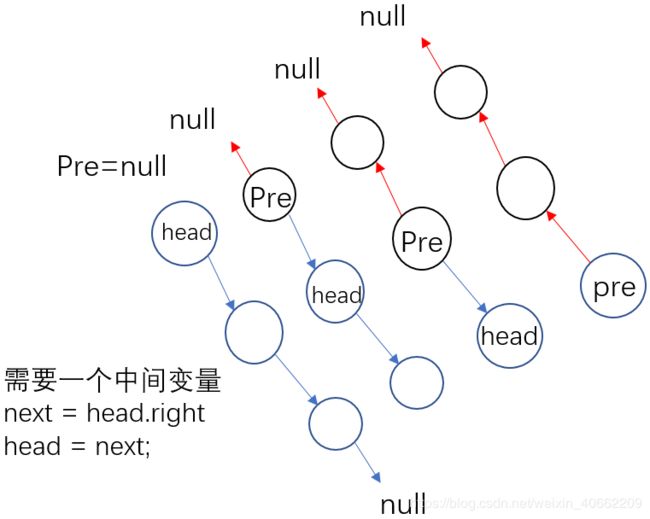
逆序右边界
public static Node reverseEdge(Node head) { //逆序打印左子树的右边界
//创建一个新的节点链
Node pre = null;
Node next = null; //中间变量
while(head!=null) {
next = head.right;
head.right = pre;
pre = head;
head = next;
}
return pre;
}
public static void morrisPos(Node head) {
//到达两次的节点,第一次到达就打印;
//到达一次的节点,直接打印
System.out.println();
if(head == null) {
return ;
}
Node cur = head;
Node mostright = null;
while(cur!=null) {
mostright = cur.left;
if(mostright!=null) {
while(mostright.right != null && mostright.right !=cur) {
mostright = mostright.right;
}
if(mostright.right == null) {
mostright.right = cur;
cur = cur.left;
continue;
}else { //cur第二次到达的时候
mostright.right = null;
printEdge(cur.left); //逆序打印左子树的右边界
}
}
//
cur = cur.right;
}
printEdge(head); //回到最后一个顶点
System.out.println();
}