Leetcode98 验证二叉搜索树 C++,Java,Python

Leetcode98 验证二叉搜索树

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/validate-binary-search-tree/

博主Github：https://github.com/GDUT-Rp/LeetCode

题目：

给定一个二叉树，判断其是否是一个有效的二叉搜索树。

假设一个二叉搜索树具有如下特征：

• 节点的左子树只包含小于当前节点的数。
• 节点的右子树只包含大于当前节点的数。
• 所有左子树和右子树自身必须也是二叉搜索树。

示例 1:

输入:
    2
   / \
  1   3
输出: true

示例 2:

输入:
    5
   / \
  1   4
     / \
    3   6
输出: false
解释: 输入为: [5,1,4,null,null,3,6]。
     根节点的值为 5 ，但是其右子节点值为 4 。

解题思路：

直观想法

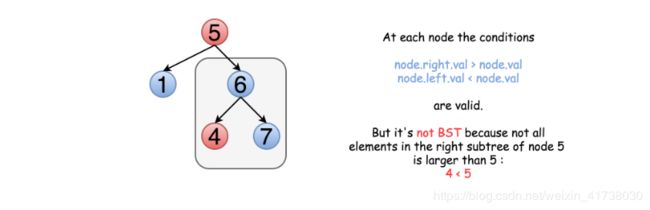
脑子第一反应，这是一个平凡的问题。只需要遍历整棵树，检查 node.right.val > node.val 和 node.left.val < node.val 对每个结点是否成立。

问题是，这种方法并不总是正确。不仅右子结点要大于该节点，整个右子树的元素都应该大于该节点。例如:

这意味着我们需要在遍历树的同时保留结点的上界与下界，在比较时不仅比较子结点的值，也要与上下界比较。

方法一：递归算法

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    bool isValidBST(TreeNode* root){
        return helper(root, LONG_MIN, LONG_MAX);
    }

    bool helper(TreeNode* node, long lower, long upper) {
        if (!node){
            return true;
        }
        if (node->val <= lower || node->val >= upper) return false;
        return helper(node->left, lower, node->val) && helper(node->right, node->val, upper);
    }
};

Java

class Solution {
  public boolean helper(TreeNode node, Integer lower, Integer upper) {
    if (node == null) return true;

    int val = node.val;
    if (lower != null && val <= lower) return false;
    if (upper != null && val >= upper) return false;

    if (! helper(node.right, val, upper)) return false;
    if (! helper(node.left, lower, val)) return false;
    return true;
  }

  public boolean isValidBST(TreeNode root) {
    return helper(root, null, null);
  }
}

Python

# -*- coding: utf-8 -*-
# @File   : LeetCode98.py
# @Author : Runpeng Zhang
# @Date   : 2020/2/18
# @Desc   : 给定一个二叉树，判断其是否是一个有效的二叉搜索树。


# Definition for a binary tree node.
class TreeNode:
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None


class Solution:
    def isValidBST(self, root: TreeNode) -> bool:
        """
        递归判断其是否是一个有效的二叉搜索树
        :rtype: bool
        """
        def helper(node, lower=float('-inf'), upper=float('inf')):
            if not node:
                return True

            val = node.val
            if val <= lower or val >= upper:
                return False

            if not helper(node.right, val, upper):
                return False
            if not helper(node.left, lower, val):
                return False
            return True

        return helper(root)

复杂度分析

• 时间复杂度 : $O(N)$。每个结点访问一次。
• 空间复杂度 : $O(N)$。我们跟进了整棵树。