一篇文章完全弄懂Logistic回归(含极大似然估计详细推导和实现代码)
别弄错了,Logistic回归是分类模型。
什么是分类问题?
在学习线性回归的时候,我们已经理解了什么是回归,回归就是确定变量之间相互依赖的定量关系的统计学方法。那么同样,在开始学习Logistic回归模型前,我们先来看看什么是分类问题。
分类相比于回归要好理解得多了,我们按照所选取的样本的属性、特征对数据集的样本进行类别的划分,这就是分类。
这里使用二分类举个例子。
上图对四个样本点,按照分类规则为若X > 0.6,则 Y = 0;否则 Y = 1,进行分类。很显然,对于二分类问题我们很直观的就能理解。使用分段函数就可以很清晰直观地表述出分类规则。如下:
为什么不使用线性回归解决分类问题?
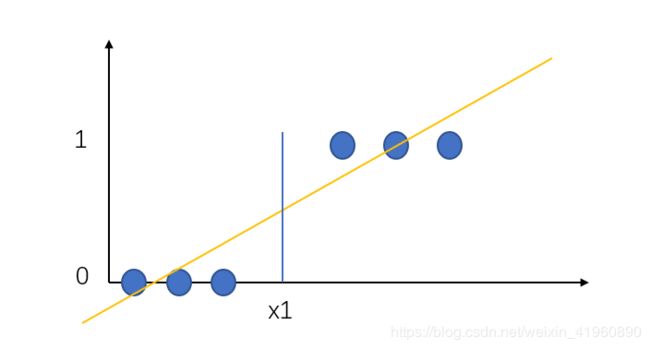
确实,在一些特别地情况下,线性回归的确可以找到分类的阈值。如果样本分布较为集中,我们的确可以使用线性回归构造一个线性方程从而找到两个类别间的区分点(阈值),如图所示。
但是,一旦样本点分布不均匀就会出现偏差了。不均匀的样本分布会导致线性方程的参数产生偏移,导致阈值x1会向分布较分散的类别倾斜,造成比较严重的误差,如图:
在y = 1 的类别中出现了一个 x 值过大的点,导致分类的阈值从原本的 x1 移动到了 x2。在这情况下已经有两个样本点已经分类错误了。
另一方面:我们希望分类模型的输出仅仅由 0 和 1 组成即可,而线性回归在趋向正无穷和负无穷的时候并没有极限,会使对应的输出有可能存在远大于 1 或者 远小于 0 的情况,这也是我们不采用线性回归的原因。
因此,我们希望在线性回归的基础上进行改进,使得样本点对应的输出限制在 0 到 1 的范围内。
Logistic回归模型
线性回归模型能够反映出变量之间的关系,而类别的划分是根据样本的属性字段相关,也就是说,样本的类别与样本的属性字段之间存在着定量的关联。因此我们需要线性回归找到类别与属性字段的关联,同时也希望函数的输出在 0 到 1 的范围内部。因此我们只需要在线性回归的基础上进行一些处理即可。首先列出线性回归的方程如下:
![]()
这假设方程当然不满足我们的需要,我们对其进行变形:
![]()
而这里的 g(x) 函数就是计算机视觉中的神器之一:Sigmoid函数
![]()
为什么选择Sigmoid函数呢?
我们来看看它的图形就知道原因了。
这里我使用了 matplotlib 完成对 Sigmoid 函数的绘制,代码如下:
import numpy as np
import matplotlib.pyplot as plt
# 这个表示在-5到5之间生成1000个x值
x=np.linspace(-5,5,1000)
# 对上述生成的1000个数循环用sigmoid公式求对应的y
y=[1/(1+np.exp(-i)) for i in x]
plt.yticks([0,0.5,1.0],[0,0.5,1.0])
#用上述生成的1000个xy值对生成1000个点
plt.plot(x,y,color='darkblue')
# plt.plot()实际上会通过plt.gca()获得当前的Axes对象ax,然后再调用ax.plot()方法实现真正的绘图。
ax=plt.gca()
#删除右边框设为无
ax.spines['right'].set_color('none')
#删除上边框设为无
ax.spines['top'].set_color('none')
# ax.xaxis.set_ticks_position('bottom')
# #调整x轴位置,在 y = 0 处
ax.spines['bottom'].set_position(('data', 0))
ax.yaxis.set_ticks_position('left')
# #调整y轴位置,在 x = 0 处
ax.spines['left'].set_position(('data', 0))
# 设置横坐标下的说明文本
plt.xlabel("sigmoid")
plt.show()图像为:
显然,这就是我们想要的!能够将线性回归输出的 Y 值很好的限制在 0 到 1 的区间内,从而很好的完成分类。
为什么Sign函数不行呢?
到这里,肯定有小伙伴问了,“我学过sign函数,他长得跟sigmoid函数很类似,也能够将 X 限制在 0 到 1 的范围内,为什么它不行呢?”
这里我们也画出 Sign函数 的图像看看,很简单,把上面 python 代码中 Y 的表达式更改如下:
y=[1 * (i > 0) for i in x]得到输出结果:
这样看起来仿佛 Sign 函数更适合分类,因为他的分类判别非常果决,只输出 0 和 1。但是为什么不选他作为 g(x) 呢?
我们知道,Logistic回归只是在线性回归上增加了一个 g(x) 的限制,而在模型训练的过程中实际上还是对线性回归中的 ![]() 进行训练。我们是怎么对线性回归中的
进行训练。我们是怎么对线性回归中的 ![]() 进行计算的?梯度下降!要使用梯度下降,就存在一个前提,即损失函数可导。而以 Sign函数 为假设函数列出来的损失函数明显在
进行计算的?梯度下降!要使用梯度下降,就存在一个前提,即损失函数可导。而以 Sign函数 为假设函数列出来的损失函数明显在 ![]() 出不可导(左导 = 0,右导 = 1)。而反观 Sigmoid函数,在
出不可导(左导 = 0,右导 = 1)。而反观 Sigmoid函数,在 ![]() 内均有导数存在,于是只能跟 Sign函数说再见了。在深度学习中,激活函数的选取也是这个道理,简单来说,就是在 0 这个点上,Sign函数会发生梯度消失的情况。
内均有导数存在,于是只能跟 Sign函数说再见了。在深度学习中,激活函数的选取也是这个道理,简单来说,就是在 0 这个点上,Sign函数会发生梯度消失的情况。
极大似然估计与交叉熵损失函数
下一步,我们要确定 Logistic回归的损失函数。很多人会以为Logistic的损失函数本身就定义成那样,但是并不是定义出来的,而是通过极大似然估计出来的。
什么是极大似然估计?(理解真的很重要!)
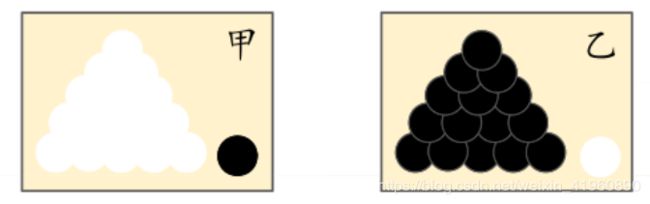
如上图,假设有两个完全一样的箱子,甲箱子中有99个白球和1个黑球;乙箱子中有99个黑球和1个白球,在一次实验中,取出了一个球是黑球,问:该黑球从哪个箱子里取出?
显然,我们会毫不犹豫地回答黑球更有可能从乙箱子中取出。这符合我们的经验事实,这里的“更有可能”类似于“极大似然”。
极大似然估计是建立在极大似然原理的基础上的一个统计方法,是概率论在统计学中的应用。极大似然估计提供了一种给定观察数据来评估模型参数的方法,即:“模型已定,参数未知”。通过若干次试验,观察其结果,利用试验结果得到某个参数值能够使样本出现的概率为最大,则称为极大似然估计。
由于样本集中的样本是独立同分布(独立说明联合分布可用乘法)的,因此,我们可以列出在样本集合 ![]() 上的的联合分布率:
上的的联合分布率:
![]()
![]()
而这个联合分布概率 ![]() 称为相对于数据集
称为相对于数据集 ![]() 的似然函数。
的似然函数。
如果 ![]() 是参数空间中能使似然函数
是参数空间中能使似然函数 ![]() 最大的
最大的 ![]() 值,则
值,则 ![]() 应该是“最可能”的参数值,那么
应该是“最可能”的参数值,那么 ![]() 就是θ的极大似然估计量。它是样本集的函数,记作:
就是θ的极大似然估计量。它是样本集的函数,记作:
![]()
理解极大似然估计以后,我们来看看他是如何估计Logistic回归的参数的。
使用极大似然估计Logistic回归参数
二分类的Logistic回归满足伯努利分布(概率论是个好东西,不会的去查查资料),于是我们不难写出分类为 0 和 1 的概率:
对上式整理一下,得到下式:
![]()
同时,![]() 的表达式如下:
的表达式如下:
![]()
再根据似然函数:
![]()
这里为了方便计算,我们对似然函数取对数(取对数并不影响我们找最大值)。于是,我们可以列出Logistic回归的似然函数为:
因此我们得到:
下一步,我们要计算 ![]() 的梯度算子,即上式对
的梯度算子,即上式对 ![]() 求导:
求导:
![]()
由此,我们可以进行下一步的梯度上升计算啦!
使用梯度上升更新参数
梯度上升跟梯度下降类似,都是通过梯度算子进行全局最小值(最大值)的搜索。
这里就不重复内容了,直接推导:
![]()
代入前面的梯度算子:
得到最最最最终的结果:
![]()
然后不断更新模型的参数 ![]() ,最终得到一个基于Logistic回归的分类模型!
,最终得到一个基于Logistic回归的分类模型!
代码实现
调用sklearn实现
import matplotlib.pyplot as plt
import numpy as np
from sklearn.linear_model import LogisticRegression
import pandas as pd
import math
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_splitcancer = load_breast_cancer()
X = cancer.data
y = cancer.target
print('data shape:{0}'.format(X.shape))
print('no.features:{0}'.format(X.shape[1]))
print('features name:{0}'.format(cancer.feature_names))
print('no.postive:{0}'.format(y[y==1].shape[0]))
print('no.negative:{0}'.format(y[y==0].shape[0]))data shape:(569, 30) no.features:30 features name:['mean radius' 'mean texture' 'mean perimeter' 'mean area' 'mean smoothness' 'mean compactness' 'mean concavity' 'mean concave points' 'mean symmetry' 'mean fractal dimension' 'radius error' 'texture error' 'perimeter error' 'area error' 'smoothness error' 'compactness error' 'concavity error' 'concave points error' 'symmetry error' 'fractal dimension error' 'worst radius' 'worst texture' 'worst perimeter' 'worst area' 'worst smoothness' 'worst compactness' 'worst concavity' 'worst concave points' 'worst symmetry' 'worst fractal dimension'] no.postive:357 no.negative:212
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size = 0.2)
model = LogisticRegression()
model.fit(X_train,y_train)
train_score = model.score(X_train,y_train)
test_score = model.score(X_test,y_test)
print('\ntrain score:{}'.format(train_score))
print('test score:{}'.format(test_score))
pre = model.predict(X_train)train score:0.967032967032967 test score:0.9385964912280702