数据结构与算法笔记(7) -字符串匹配算法之KMP算法

1. 朴素匹配算法

朴素匹配算法，也常称之为暴力匹配算法，将模式字符串 p 和目标字符串 t 左端对齐，逐位比较，如果匹配失败，则将p右移一位，从p的首端再次开始逐位比较，知道匹配成功。

现在有目标字符串 t (“ABCDAB ABCDABC ABCDABD”) 和模式字符串 p (“ABCDABD”)，需要在 t 中匹配 p，那么将 t 和 p 左端对齐，逐位比较，如下图所示：

当匹配到空格不等于字符D时，将 p 右移一位，依旧从 p 的左端开始匹配。

第一个字符 A 不等于目标字符串中的 B，匹配失败，右移一位，很明显，需要移动三次，中间两次不上图了，直接看移动到目标字符串 t 的下标为4的位置：

这里，匹配到 p 的第三个字符 C 时匹配失败，那么，继续将p又移一位，知道匹配成功为止。

原理讲完了，那么实际操作一下，使用python实现如下:

In [1]: def violent_search(t, p):
   ...:     len_t = len(t)
   ...:     len_p = len(p)
   ...:     i, j = 0, 0
   ...:     while i < len_t and j < len_p:
   ...:         if t[i] == p[j]:
   ...:             i, j = i+1, j+1
   ...:         else:
   ...:             i = i - j + 1
   ...:             j = 0
   ...:     if j == len_p:
   ...:         return i-j
   ...:     return -1
   ...:
In [2]: t = 'ababcabcd'
In [3]: p = 'abcd'
In [4]: ret = violent_search(t, p)
In [5]: ret
Out[5]: 5

该算法需要遍历目标字符串和模式字符串，设目标字符串的规模为n, 模式字符串的规模为m, 易知最坏时间复杂度 O(m*n)。

2. KMP 算法

对于上面的朴素匹配算法，效率显然很低，因为进行了很多看起来没有意义的匹配，那么，在我们看来没有意义的匹配是否可以直接跳过呢？比如下面这样，从状态(1)直接跳到状态(2)：

可以看到，在字符串 p 匹配到字符 D 时匹配失败，此时可以将字符串 p 右移，明显可以知道右移1位，2位，3位都是匹配失败，只有移动到到目标字符串下标是4的位置时才开始匹配成功，而且不会导致目标字符串 t 回溯，在这个位置，模式字符串的 C 处于上一次匹配失败的点，而 C 前面的 A 和 B 是和目标字符串具有相同的字符 A，B。也就是说，移动之后，只需要将 p 中的 C 和上一次实配点进行匹配就可以了。
那么，小小的总结一下，匹配失败时，需要将模式字符串向右移动，此时，需要找到失配点前目标字符串和模式字符串前缀最长的相同的字符串即可。也就是找到模式字符串最大公共前后缀。
按照这个逻辑，继续匹配:

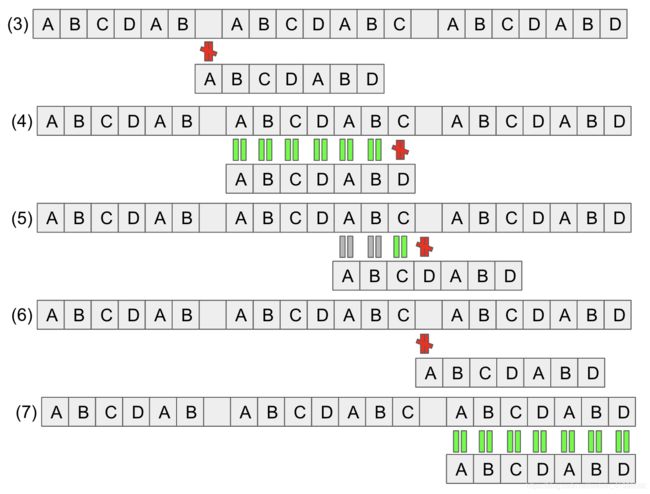
kmp算法的基本想法就是不回溯。在 p_i 匹配 t_j 失败时，i 能有一个对应的 k 值，下一步使 p_k 和 t_j 进行比较即可。也就是让模式字符串前移若干位置。我们先不考虑如何求出这样一个k值的表，先假设已经有了这样的表 pnext。那么，按照我们的思路就可以完成匹配算法:

In [1]: def kmp_search(text, pattern, pnext):
   ...:     len_t = len(text)
   ...:     len_p = len(pattern)
   ...:     i, j = 0, 0
   ...:     while i < len_t and j < len_p:
   ...:         if j == -1 or text[i] == pattern[j]:
   ...:             i, j = i+1, j+1
   ...:         else:
   ...:             j = pnext[j]
   ...:     if j == len_p:
   ...:         return i-j
   ...:     return -1
   ...:

算法中有判断 j==-1 的情况，想一下，对于模式字符串的首字符，只要匹配失败就需要将模式字符串前移一位，所以之前进行的任何匹配都是没有意义的，所以这里设置为-1，只要遇见-1，那么前移即可。

现在考虑如何构造 pnext 表呢？也就是如何求最长公共前后缀呢？
构造pnext表采用了递推法，其实很简单，看完之后你会发现和上面的匹配过程是一模一样。
假设，我们在计算某个位置的最长公共前后缀，我们已经知道 pnext[i-1] = k，那么开始比较 p[i] 和 p[k]，如果相等，则 k 肯定 +1 ；那么如果不相等呢？看下图：

看完图，应该能明白吧，当p[i] != p[k]时，想找最长公共前后缀，如果笨一点就是把字符串前移一位，然后追对匹配，但是显然，对于适配点前面的字符串都是匹配过的，所以只要让字符串前移指定的位数即可，这个位数就是C对应的k值，(因为在匹配点之前我们都已经计算过了k值了)。所以，这里让 k=next[k] 的意义就是让字符串前移到更小的相等的前后缀的位置。
所以，next数组和前缀表的关系就如下图:

上代码：

In [2]: def pattern_next(pattern):
   ...:     len_p = len(pattern)
   ...:     pnext = [-1] * len_p
   ...:     k = -1
   ...:     i = 0
   ...:     while i < len_p - 1:
   ...:         if k == -1 or pattern[k] == pattern[i]:
   ...:             i, k = i+1, k+1
   ...:             pnext[i] = k
   ...:         else:
   ...:             k = pnext[k]
   ...:     return pnext
   ...:

这个算法还可以继续优化一下，对于上面的例子，在推导next数组中D对应的k值的时候，这个时候如果D和目标字符串匹配时失败。那么，应该找到D前面的子串具有的最大公共前后缀长度，但实际上，我们这个时候已经知道了目标字符串肯定不等于D，那么如果此时将模式字符串前移之后，也肯定是不匹配的，所以，不如直接让我们的next表的k值就设置为下一个字符的k值。

In [2]: def pattern_next(pattern):
   ...:     len_p = len(pattern)
   ...:     pnext = [-1] * len_p
   ...:     k = -1
   ...:     i = 0
   ...:     while i < len_p - 1:
   ...:         if k == -1 or pattern[k] == pattern[i]:
   ...:             i, k = i+1, k+1
   ...:             if pattern[i] == pattern[k]:
   ...:                 pnext[i] = pnext[k]
   ...:             else:
   ...:                 pnext[i] = k
   ...:         else:
   ...:             k = pnext[k]
   ...:     return pnext
   ...: