用神经网络拟合初等函数

引言

从理论上讲，感知机和激活函数的组合可以拟合任意函数。

本文利用神经网络拟合一个初等函数。

语言与外部库

使用python语言，涉及的外部库有：

• keras 简明神经网络框架
• math  标准数学库
• numpy 大型数组计算支持
• matplotlib 绘图工具包

拟合目标

目标函数为一个自定义初等函数，代码如下：

def my_function(x):
    def f(x):
        if x < -1:
            return -.2 *x + 3
        elif -1 <= x and x < 0:
            return math.sin(x)
        elif 0 <= x and x < 5:
            return math.sqrt(x)
        elif 5 <= x:
            return 3
    y = np.zeros_like(x)
    for i in range(len(x)):
        y[i] = f(x[i])
    return y

注意，嵌套函数定义是为了支持与numpy数组的交互。

数据采集

直接从拟合目标中生成样本：

x = np.arange(-10, 10, .00001)
y = my_function(x)

绘图：

抽取一部分作为训练样本：

x_train = x[::2]
y_train = y[::2]

模型设计

使用两个全连接隐藏层，配合relu作激活函数，加入随机失活，输出层不带激活函数。相应keras代码如下：

model = models.Sequential()
model.add(layers.Dense(1, activation='relu', input_shape=(1,)))
model.add(layers.Dense(128, activation='relu'))
model.add(layers.Dense(128, activation='relu'))
model.add(layers.Dropout(.2))
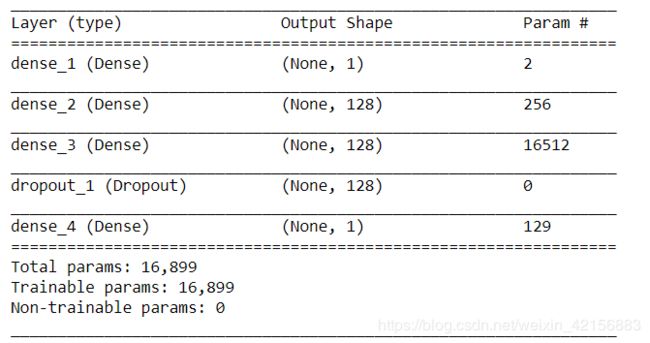
model.add(layers.Dense(1))

模型总览：

一共有16, 899个参数，同样规模的网络已经可以识别手写数字（数据集：MINIST）。

按照回归问题的惯例配置优化器和损失函数：

model.compile(optimizer='rmsprop',
              loss='mse',
              metrics=['mae'])

训练

10, 000个样本一组，迭代100次，刚好把1, 000, 000个样本浏览一遍（平均而言）。

history = model.fit(x_train,
                    y_train,
                    epochs=100,
                    batch_size=10000,
                    )
model.save('mathImitation') # 道路千万条，安全第一条；
                            # 训练不保存，丢失两行泪。

训练结果

对每一轮迭代的平均绝对误差绘图：

可见，误差呈下降趋势。

测试

在原样本上测试数据（注意，通常不能在包含训练数据的样本集里测试）：

test_mse_score, test_mae_score = model.evaluate(x, y)

得到结果，test_mae_score为

0.05494211483037472

也就是说，平均绝对误差不超过0.05。

生成

将神经网络的拟合结果绘出：

可见，与my_function已经十分接近。观察发现，误差集中在以下两处：

泛化 

• 左起第一个分段点处，拟合结果是平滑的，原函数是跳跃的（相对而言）
• 区间[-1, 5)中，没有突出x=0左右是两个不同的函数。也有平滑化的误差。

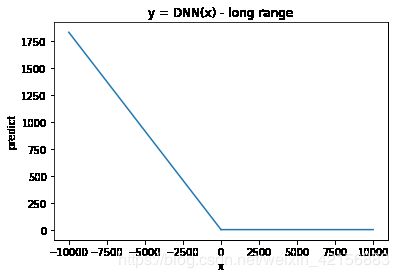
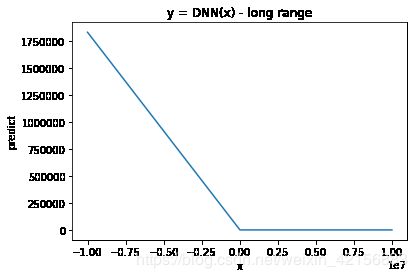
用远大于训练，结果直到[-10000000, 10000000)，结果都保持在L型。下面分别是x范围取[-10000, 10000)与[-10000000, 10000000)时的生成函数图像

 

不得不说，该网络展现出了令我惊讶的泛化能力，因为[-10000000, 10000000)已经远远超出了训练数据的范围。 我最初预计拟合结果在训练数据之外的地方会严重偏离目标，因为训练数据中有很大一部分并不是直线。

总结

神经网络以其在图像识别上巨大的成功闻名天下。通过拟合初等函数的实验，一窥其“万能函数拟合器”的核心作用。