【机器学习】PCA原理解释及其在MNIST上的应用
预备知识:
什么是协方差:https://blog.csdn.net/GoodShot/article/details/79940438
什么是协方差矩阵:https://baike.baidu.com/item/%E5%8D%8F%E6%96%B9%E5%B7%AE%E7%9F%A9%E9%98%B5/9822183?fr=aladdin
tf.svd:
https://www.jianshu.com/p/107196a8f7f0
PCA形象解释:
https://www.cnblogs.com/LeftNotEasy/archive/2011/01/19/svd-and-applications.html
tf.slice:
https://www.jianshu.com/p/71e6ef6c121b
__init__(self) :
https://blog.csdn.net/m0_37693335/article/details/82972925
PCA(Principal component analysis)主成分分析
1.基本思想:
利用正交变换把由线性相关变量表示的观测数据转换为少数几个由线性无关变量表示的数据,线性无关的变量称为主成分。
2.方法
求主成分→求特征向量
设x是m维随机变量,![]() 是x的协方差矩阵,
是x的协方差矩阵,![]() 的特征值分别是
的特征值分别是![]() ,特征值对应的单位特征向量分别是
,特征值对应的单位特征向量分别是![]() ,则x的第k主成分是:
,则x的第k主成分是:
![]()
协方差矩阵的特征向量不好计算:求特征向量→SVD求矩阵本身奇异值
![]()
列压缩:![]()
行压缩:![]()
3.代码
这份代码是我在一个教程上看到的,但是明显缺少了一些东西,我又在网上翻了翻才在Github上找到原来的代码。原来用的是鸢尾花数据集,教程上是mnist数据集,读取完Datasets后用mnist.train.images和mnist.train.labels读取array格式的数据,在这一步也费了不少时间><
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import seaborn as sns
from sklearn import datasets
import os
os.environ['CUDA_VISIBLE_DEVICES'] = '1'
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("MNIST_data/")
class TF_PCA:
def __init__(self, data, target = None, dtype = tf.float32):
self._data = data
self._dtype = dtype
self._target = target
self._graph = None
self._X = None
self._u = None
self._singular_values = None
self._sigma = None
def fit(self):
self._graph = tf.Graph()#tf.Graph() 表示实例化了一个类,一个用于 tensorflow 计算和表示用的数据流图
with self._graph.as_default():#定义图
self._X = tf.placeholder(self._dtype, shape = self._data.shape)
#print(self._data.shape)
# Perform SVD对X进行奇异值分解
singular_values, u, _ = tf.svd(self._X)
# Create sigma matrix
sigma = tf.diag(singular_values)#返回具有给定对角线值的对角张量
print('sigma:',sigma)
with tf.Session(graph = self._graph) as sess:#定义计算
self._u, self._singular_values, self._sigma = sess.run([u, singular_values, sigma], feed_dict = {self._X:self._data})
def reduce(self, n_dimensions = None, keep_info = None):
if keep_info:
# Normalize singular values
normalized_singular_values = self._singular_values/sum(self._singular_values)
#information per dimension
info = np.cumsum(normalized_singular_values)#按照所给定的轴参数返回元素的梯形累计和
#Get the first index which is above the given infomation threshold
it = iter(idx for idx, value in enumerate(info) if value >= keep_info)
#iter()获取可迭代对象的迭代器
n_dimensions = next(it) + 1
with self._graph.as_default():
# Cut out the relevant part from digma
sigma = tf.slice(self._sigma, [0,0], [self._data.shape[1], n_dimensions])
print('sigma(after svd):',sigma)
#tf.slice(t,begin,size)切片
# PCA
pca = tf.matmul(self._u, sigma)
with tf.Session(graph = self._graph) as session:
return session.run(pca, feed_dict = {self._X:self._data})
tf_pca = TF_PCA(mnist.train.images, mnist.train.labels)#实例化一个类
tf_pca.fit()
pca = tf_pca.reduce(keep_info = 0.8) # The reduce dimensions dependent upon the % of information
print('original data shape:', mnist.train.images.shape)
print('reduced data shape:', pca.shape)
Set = sns.color_palette("Set2", 10)#调色板,10种颜色
color_mapping = {key:value for (key, value) in enumerate(Set)}#color_mapping创建颜色字典
colors = list(map(lambda x: color_mapping[x], mnist.train.labels))#将每个样本的标记映射到相应的颜色
fig = plt.figure()
ax = Axes3D(fig)
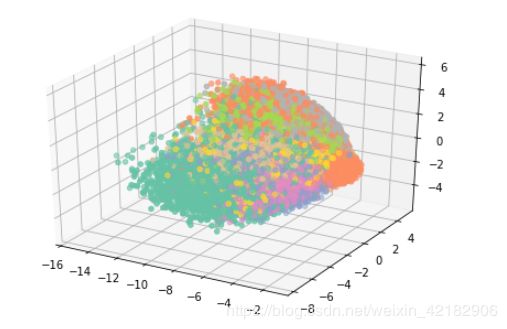
ax.scatter(pca[:,0], pca[:,1], pca[:,2], c = colors)#绘制散点图,用前三个特征描述十个数字mnist里面一张图像的大小是28*28=784,也就是说原来一张图片由784个特征来描述,PCA降维后变成了231。
取前三个特征,可以看出数字大致被区分开了。