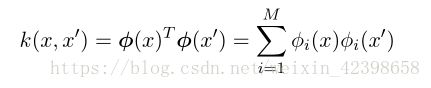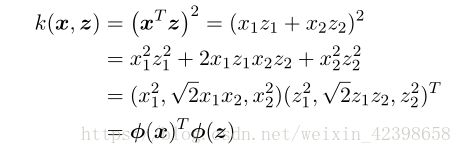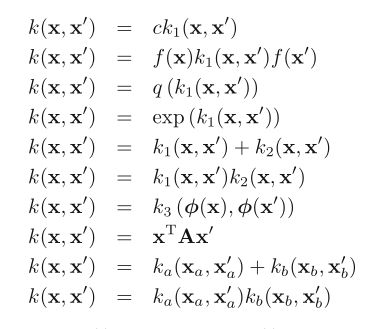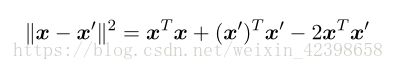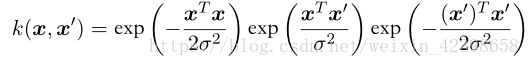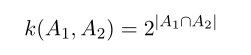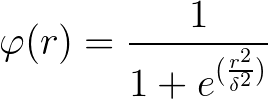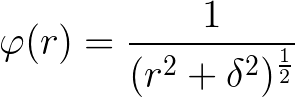机器学习--支持向量机（六）径向基核函数（RBF）详解

前面讲解了什么是核函数，以及有效核函数的要求，到这里基本上就结束了，很多博客也是如此，但是呢这些只是理解支持向量机的原理，如何使用它讲解的却很少，尤其是如何选择核函数更没有人讲，不讲也是有原因的，因为核函数的选择没有统一的定论，这需要使用人根据不同场合或者不同问题选择核函数，选择的标准也没有好的指导方法，一般都是尝试使用，所以选择核函数就需要看使用者的经验了，研究者们也在一直研究这种方法，这方面的研究称为核工程，因为核函数不仅仅使用在支持向量机中，只要满足多维数据的內积即可使用核函数进行解决，因此核函数可以和很多算法结合，能产生意想不到的效果，，但是核函数因为太过庞大，我在这里只是引导的讲解一下，以后有时间专门开一个栏目专讲核函数的选择，在这里只简单的讲解一下核函数，同时深入讲解径向基核函数，通过讲解这一个核函数，希望大家可以通过这种方法去学习如何选择核函数，当然最后我会把sklearn的核函数的api接口也讲解一下，虽然还没使用过，但是当理解径向基核函数后，还是可以很容易使用的，好，废话不多说了，下面就开始进入正题：

在讲径向基核函数之前，先给大家讲解一下，核函数构造方法：

为了利⽤核替换，我们需要能够构造合法的核函数。⼀种⽅法是选择⼀个特征空间映射 ϕ(x) ，然后使⽤这个映射寻找对应的核，这⾥，⼀维空间的核函数被定义为：

其中 ϕ i (x) 是基函数。

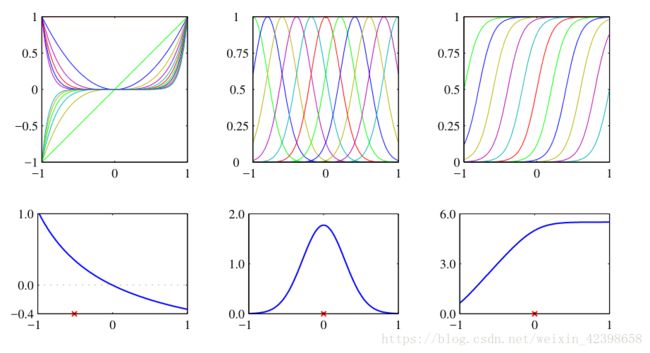
上图从对应的基函数集合构建核函数的例⼦。在每⼀列中，下图给出了由上面公式定义的核函数 k(x,x ′ ) ，它是 x 的函数， x ′ 的值⽤红⾊叉号表⽰，⽽上图给出了对应的基函数，分别是多项式基函数（左列）、⾼斯基函数（中列）、 logistic sigmoid 基函数（右列）。 

另⼀种⽅法是直接构造核函数。在这种情况下，我们必须确保我们核函数是合法的，即它对应于某个（可能是⽆穷维）特征空间的标量积。作为⼀个简单的例⼦，考虑下⾯的核函数：

 如果我们取⼆维输⼊空间 x = (x 1 ,x 2 ) 的特殊情况，那么我们可以展开这⼀项，于是得到对应的⾮线性特征映射：

我们看到特征映射的形式为  ，因此这个特征映射由所有的⼆阶项组成，每个⼆阶项有⼀个具体的系数。但是，更⼀般地，我们需要找到⼀种更简单的⽅法检验⼀个函数是否是⼀个合法的核函数，⽽不需要显⽰地构造函数 ϕ(x) 。核函数 k(x,x ′ ) 是⼀个合法的核函数的充分必要条件是 Gram 矩阵（元素由 k(x n ,x m ) 给出）在所有的集合 {x n } 的选择下都是半正定的。注意，⼀个半正定的矩阵与元素全部⾮负的矩阵不同。
构造新的核函数的⼀个强⼤的⽅法是使⽤简单的核函数作为基本的模块来构造。可以使⽤下⾯的性质来完成这件事。
给定合法的核 k 1 (x,x ′ ) 和 k 2 (x,x ′ ) ，下⾯的新核也是合法的 ：

通过上面核函数的性质就可以构造出不同的核函数了，但是最好还是验证一下是否是有效的核函数 ，即核矩阵是对称的半正定矩阵，下面简单证明一下径向基核函数是有效的，然后再详解径向基核函数的来源和应用：

这个经常被称为⾼斯核。但是注意，在我们现在的讨论中，它不表⽰概率密度，因此归⼀化系数被省略了。这是⼀个合法的核，理由如下。我们把平⽅项展开 ：

从而：

 通过上面的性质以及线性核 的合法性，即可看到⾼斯核是⼀个合法的核。注意，对应于⾼斯核的特征向量有⽆穷的维数。那么你可以在此基础继续变化构造适合自己的核函数：

⾼斯核并不局限于使⽤欧⼏⾥得距离。如果我们使⽤公式|x-x‘|中的核替换，将 x T x ′ 替换为⼀个⾮线性核 κ(x,x ′ ) ，我们有

 核观点的⼀个重要的贡献是可以扩展到符号化的输⼊，⽽不是简单的实数向量。核函数可以定义在多种对象上，例如图⽚、集合、字符串、⽂本⽂档。例如，考虑⼀个固定的集合，定义⼀个⾮向量空间，这个空间由这个集合的所有可能的⼦集构成。如果 A 1 和 A 2 是两个这样的⼦集，那么核的⼀个简单的选择可以是：

其中 A 1 ∩ A 2 表⽰集合 A 1 和 A 2 的交集， |A| 表⽰ A 的元素的数量。这是⼀个合法的核，因为可以证明它对应于⼀个特征空间中的⼀个内积。 

当然还有其他的方法构造核函数例如从⼀个概率⽣成式模型开始构造，有兴趣的同学可以研究一下.

下面就详解什么是径向基核函数，将对他的由来和使用进行全面阐释：

什么是径向基函数？

理解RBF网络的工作原理可从两种不同的观点出发：①当用RBF网络解决非线性映射问题时，用函数逼近与内插的观点来解释，对于其中存在的不适定(illposed）问题，可用正则化理论来解决；②当用RBF网络解决复杂的模式分类任务时，用模式可分性观点来理解比较方便，其潜在合理性基于Cover关于模式可分的定理。下面阐述基于函数逼近与内插观点的工作原理。
          1963年Davis提出高维空间的多变量插值理论。径向基函数技术则是20世纪80年代后期，Powell在解决“多变量有限点严格（精确）插值问题”时引人的，目前径向基函数已成为数值分析研究中的一个重要领域。
         考虑一个由N维输人空间到一维输出空间的映射。设N维空间有P个输人向量平，P=1，2，....，P，它们在输出空间相应的目标值为，P对输人一输出样本构成了训练样本集。插值的目的是寻找一个非线性映射函数F(X),使其满足下述插值条件：

                                                                                                        

式子中，函数F描述了一个插值曲面，所谓严格插值或精确插值，是一种完全内插，即该插值曲面必须通过所有训练数据点。

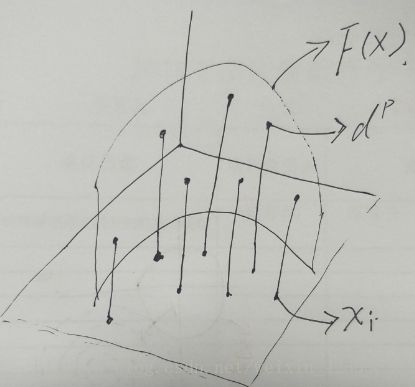
那么到底什么是差值，在这里简单的解释一下，就是通过训练集数据，我找到一个曲面，这个曲面可以完全覆盖这些训练点，那么找到这个曲面后就可以通过这个曲面取寻找其他的值了，下面画个图给大家看看：

 

画图不是很好啊，意思差不多，就是我通过一些数据样本点 ，每个样本都有目标值，通映射高维空间去找到一个曲面F(x),这个曲面需要经过所有的数据，一旦这个曲面确定以后，我就可以通过这个曲面去生成更多的数据目标值，就是这个意思了，好，我们继续往下：

采用径向基函数技术解决插值问题的方法是，选择P个基函数个训练数据，各基函数的形式为：
                                                                                                   
式中，基函数为非线性函数，训练数据点是的中心。基函数以输人空间的点x与中心的距离作为函数的自变量。由于距离是径向同性的，故函数被称为径向基函数。基于径向基函数技术的差值函数定义为基函数的线性组合：

                                                                                                          

 在这里需要解释一下这是范数，在平面几何的向量来说就是模，然而一旦维度很高就不知道是什么东西了，可能是衡量距离的一个东西，那么这个代表什么意思呢？简单来说就是一个圆而已，在二维平面，就是圆心，x就是数据了，这个数据距离圆心的距离，因为和数据的位置和大小无关，只和到圆心的半径有关，况且同一半径圆上的点到圆心是相等的因此取名为径向，代入映射函数就是径向基函数了，我们看看径向基函数有什么特点：

将（1）式的插值条件代入上式，得到P个关于未知系数,的线性方程组：

                                                    

                                                     

                                                                            

                                                                                         

令则上述方程组可改写为：

                                                                    

令表示元素的PxP阶矩阵，和分别表示系数向量和期望输出向量，（5）式还可以写成下面的向量形式：

                                                                                                                                  

式中，称为插值矩阵，若为可逆矩阵，就可以从（6）式中解出系数向量，即：

                                                                                                                              

通过上面大家可以看到为了使所有数据都在曲面还需要系数调节，此时求出系数向量就求出了整个的映射函数了，下面在看看几个特殊的映射函数:

(1)高斯径向基函数

                                                                   

 

 横轴就是到中心的距离用半径r表示，如上图，我们发现当距离等于0时，径向基函数等于1，距离越远衰减越快，其中高斯径向基的参数在支持向量机中被称为到达率或者说函数跌落到零的速度。红色=1，蓝色=5，绿色=0.5，我们发现到达率越小其越窄。

（2） 反演S型函数

                                                          

 

 

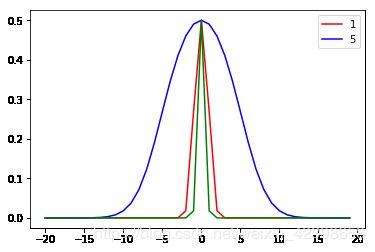
这个和径向基类似，只是极值为0.5.前面乘上系数就好了 ，红色=1，蓝色=5，绿色=0.5

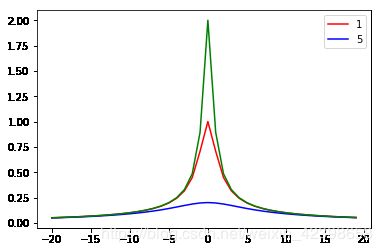
（3）拟多二次函数

                                                 

                                                                

红色=1，蓝色=5，绿色=0.5,横轴为距离r。 

径向基函数就讲完了，后面就是如何使用径向基函数进行机器学习分类呢？在这里以sklearn为例进行讲解：

核函数 可以是以下任何形式：:

• 线性: .
• 多项式: .  是关键词 degree,  指定 coef0。
• rbf: .  是关键词 gamma, 必须大于 0。
• sigmoid (), 其中  指定 coef0。

此时大家应该能看懂径向基中的函数是什么意思吧，这里我们着重讲解径向基核函数 

初始化时，不同内核由不同的函数名调用:

>>> linear_svc = svm.SVC(kernel='linear')
>>> linear_svc.kernel
'linear'
>>> rbf_svc = svm.SVC(kernel='rbf')
>>> rbf_svc.kernel
'rbf'

当用径向基（RBF）内核去训练SVM，有两个参数必须要去考虑：C惩罚系数和gamma。参数C，通用在所有SVM内核，与决策表面的简单性相抗衡，可以对训练样本的误分类进行有价转换。较小的C会使决策表面更平滑，同时较高的C旨在正确地分类所有训练样本。Gamma定义了单一训练样本能起到多大的影响。较大的gamma会更让其他样本受到影响。

直观地，该gamma参数定义了单个训练样例的影响达到了多远，低值意味着“远”，高值意味着“接近”。所述gamma参数可以被看作是由模型支持向量选择的样本的影响的半径的倒数。

该C参数将训练样例的错误分类与决策表面的简单性相对应。低值C使得决策表面平滑，而高度C旨在通过给予模型自由选择更多样本作为支持向量来正确地对所有训练样本进行分类。

 

代码就不贴了，后面有时间使用sklearn进行分类实践其实主要想说的是如果使用我们如何选择参数值，这个官方给了示例：

官方使用的数据是iris数据分类，通过交叉验证给出了热图，下面分析一下，代码下面贴，或者直接去官网复制

这个图分别是径向基两个参数的关系是如何影响正确率的，右边的颜色条书面正确率的，最下面即暗黑色正确率只有0.2，黄色接近0.98，而白色说明是1即百分百正确，大家可以看看一般参数在在哪些位置位置合适， 是c在1到100，gamma在0.001到0.1这些参数的的准确率为100%，具体的请参考官方文档。

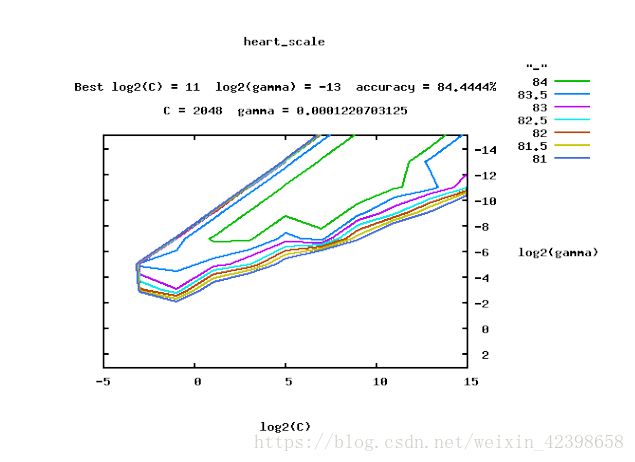
我们再看这个数据图：

这个是通过参数选择工具进行帮助选择的， sklearn.model_selection.GridSearchCV，

具体参考这篇文章https://www.csie.ntu.edu.tw/~cjlin/papers/libsvm.pdf

一般我们选择参数可以依靠参数优化工具帮我们选择，或者拿来参考都是不错的选择，在这里就详细说了，感兴趣的同学可以参考官方说明：sklearn官方网站

以上几节是完全理论的分析下面就根据机器学习实战实现一遍。

 

 

 

print(__doc__)

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import Normalize

from sklearn.svm import SVC
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import load_iris
from sklearn.model_selection import StratifiedShuffleSplit
from sklearn.model_selection import GridSearchCV


# Utility function to move the midpoint of a colormap to be around
# the values of interest.

class MidpointNormalize(Normalize):

    def __init__(self, vmin=None, vmax=None, midpoint=None, clip=False):
        self.midpoint = midpoint
        Normalize.__init__(self, vmin, vmax, clip)

    def __call__(self, value, clip=None):
        x, y = [self.vmin, self.midpoint, self.vmax], [0, 0.5, 1]
        return np.ma.masked_array(np.interp(value, x, y))

# #############################################################################
# Load and prepare data set
#
# dataset for grid search

iris = load_iris()
X = iris.data
y = iris.target

# Dataset for decision function visualization: we only keep the first two
# features in X and sub-sample the dataset to keep only 2 classes and
# make it a binary classification problem.

X_2d = X[:, :2]
X_2d = X_2d[y > 0]
y_2d = y[y > 0]
y_2d -= 1

# It is usually a good idea to scale the data for SVM training.
# We are cheating a bit in this example in scaling all of the data,
# instead of fitting the transformation on the training set and
# just applying it on the test set.

scaler = StandardScaler()
X = scaler.fit_transform(X)
X_2d = scaler.fit_transform(X_2d)

# #############################################################################
# Train classifiers
#
# For an initial search, a logarithmic grid with basis
# 10 is often helpful. Using a basis of 2, a finer
# tuning can be achieved but at a much higher cost.

C_range = np.logspace(-2, 10, 13)
gamma_range = np.logspace(-9, 3, 13)
param_grid = dict(gamma=gamma_range, C=C_range)
cv = StratifiedShuffleSplit(n_splits=5, test_size=0.2, random_state=42)
grid = GridSearchCV(SVC(), param_grid=param_grid, cv=cv)
grid.fit(X, y)

print("The best parameters are %s with a score of %0.2f"
      % (grid.best_params_, grid.best_score_))

# Now we need to fit a classifier for all parameters in the 2d version
# (we use a smaller set of parameters here because it takes a while to train)

C_2d_range = [1e-2, 1, 1e2]
gamma_2d_range = [1e-1, 1, 1e1]
classifiers = []
for C in C_2d_range:
    for gamma in gamma_2d_range:
        clf = SVC(C=C, gamma=gamma)
        clf.fit(X_2d, y_2d)
        classifiers.append((C, gamma, clf))

# #############################################################################
# Visualization
#
# draw visualization of parameter effects

plt.figure(figsize=(8, 6))
xx, yy = np.meshgrid(np.linspace(-3, 3, 200), np.linspace(-3, 3, 200))
for (k, (C, gamma, clf)) in enumerate(classifiers):
    # evaluate decision function in a grid
    Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)

    # visualize decision function for these parameters
    plt.subplot(len(C_2d_range), len(gamma_2d_range), k + 1)
    plt.title("gamma=10^%d, C=10^%d" % (np.log10(gamma), np.log10(C)),
              size='medium')

    # visualize parameter's effect on decision function
    plt.pcolormesh(xx, yy, -Z, cmap=plt.cm.RdBu)
    plt.scatter(X_2d[:, 0], X_2d[:, 1], c=y_2d, cmap=plt.cm.RdBu_r,
                edgecolors='k')
    plt.xticks(())
    plt.yticks(())
    plt.axis('tight')

scores = grid.cv_results_['mean_test_score'].reshape(len(C_range),
                                                     len(gamma_range))

# Draw heatmap of the validation accuracy as a function of gamma and C
#
# The score are encoded as colors with the hot colormap which varies from dark
# red to bright yellow. As the most interesting scores are all located in the
# 0.92 to 0.97 range we use a custom normalizer to set the mid-point to 0.92 so
# as to make it easier to visualize the small variations of score values in the
# interesting range while not brutally collapsing all the low score values to
# the same color.

plt.figure(figsize=(8, 6))
plt.subplots_adjust(left=.2, right=0.95, bottom=0.15, top=0.95)
plt.imshow(scores, interpolation='nearest', cmap=plt.cm.hot,
           norm=MidpointNormalize(vmin=0.2, midpoint=0.92))
plt.xlabel('gamma')
plt.ylabel('C')
plt.colorbar()
plt.xticks(np.arange(len(gamma_range)), gamma_range, rotation=45)
plt.yticks(np.arange(len(C_range)), C_range)
plt.title('Validation accuracy')
plt.show()